RD Sharma Solutions for Class 9 Chapter 24 Measures of Central Tendency Exercise 24.1

Chapter 24 Measures of Central Tendency RD Sharma Solutions Exercise 24.1 Class 9 Maths

Chapter Name	RD Sharma Chapter 24 Measures of Central Tendency Exercise 24.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 24.2 Exercise 24.3
Related Study	NCERT Solutions for Class 10 Maths

Exercise 24.1 Solutions

1. If the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively, find the mean height.

Solution 

It is given that, 
The heights of 5 persons are - 140 cm, 150 cm, 152 cm, 158 cm and 161 cm. 
∴ Mean height = Sum of heights/Total No. of persons 
= (140 + 150 + 152 + 158 + 161)/5
= 761/5
= 152.2

2. Find the mean of 994, 996, 998, 1002 and 1000.

Solution

Given numbers are 994, 996, 998, 1000 and 1002.
∴ Mean = Sum of Numbers/Total Numbers 
= (994 + 996 + 998 + 1000 + 1002)/5 
= 4990/5 
= 998

3. Find the mean of first five natural numbers. 

Solution

Given that, 
The first five natural numbers are 1, 2, 3, 4, 5 
∴ Mean  = Sum of Numbers/Total Numbers 
= (1 + 2 + 3 + 4 + 5)/5 
= 15/5
Mean = 3

4. Find the mean of all factors of 10 .

Solution

All factors of 10 are 1, 2, 5, 10
∴ Mean = Sum of factors/Total factors 
= (1 + 2 + 5 + 12)/4 
= 18/4 
= 9/2 = 4.5 
∴ Mean = 4.5

5. Find the mean of first 10 even natural numbers. 

Solution

Given that, 
The first 10 natural numbers be 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
∴ Mean = Sum of all Numbers/Total numbers 
= (2+4+6+8+10+12+14+16+18+20)= 110/10
= 110/10 = 11
∴ Mean  = 11

6. Find the mean of x, x+2, x  + 4, x + 6, x + 8.

Solution

Numbers  be x, x+2, x  + 4, x + 6 and  x + 8.
∴ Mean = Sum of numbers/Total numbers 
= (x + x + 2 + x + 4 + x + 6 + x + 8)/5
= (5x + 20)/5
= 5(x + 4)/5
= x + 4

7. Find the mean of first five multiples of 3.

Solution

First five multiple of 3 :  3,6,9,12,15
∴ Mean = Sum of Numbers/Total Numbers 
= (3 + 6 + 9 + 12 + 15)/5
= 45/9

8. Following are the weights (in kg) of 10 new born babies in a hospital on a particular day. 
3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6. Find the mean X .

Solution

The weight (in kg) of 10 new born babies
3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6
∴ Mean (x ) = Sum of weights/Total babies 
= 3.4+ 3.6 + 4.2 + 4.5 + 3.9 + 4.1 + 3.8 + 4.5 + 4.4 + 3.6)/10
= 40/10 = 4 kg

9. The percentage of marks obtained by students of a class in mathematics are : 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1. Find their mean.

Solution

The percentage marks obtained by students are = 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1
∴ Mean marks = (64+ 36 + 47 + 23 + 0 + 19 + 81 + 93 + 72 + 35 + 3 + 1)/12
= 474/12 = 39.5
∴ Mean marks = 39.5

10. The numbers of children in 10 families of a locality are : 
2, 4, 3, 4, 2, 0, 3, 5, 1, 1, 5. Find the mean number of children per family.

Solution

The number of children in 10 families is  2,4,3,4,2,3,5,1,1,5.
∴ Mean number of children per family 
= Total no. of children /Total families 
= (2 + 4 + 3 + 4 +2 + 3 + 5 + 1 + 1 + 5)/10
= 30/10
= 3

11. If M is the mean of x₁ , x₂ , x₃ ,x₄ ,x₅ and x₆ prove that
(x₁ - M) + (x₂ - M) + (x₃ - M) + (x₄ - M) + (x₅ - M) + (x₆ - M) = 0.

Solution

12. Durations of sunshine (in hours) in Amritsar for first 10 days of August 1997 as reported by

the Meteorological Department are given below:

9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9

(i) Find the mean x 
(ii) Verify that 

Solution

Duration of sunshine (in hours) for 10 days are = 9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9

(i) Mean x = Sum of all numbers/Total numbers 

= (9.6 + 5.2 + 3.5 + 1.5 + 1.6 + 2.4 + 2.6 + 8.4 + 10.3 + 10.9)/10
= 56/10 = 5.6

13. Explain, by taking a suitable example, how the arithmetic mean alters by

(i) adding a constant k to each term,

(ii) subtracting a constant k from each them,

(iii) multiplying each term by a constant k and,

(iv) dividing each term by a non-zero constant k.

Solution

Let us say numbers are be 3, 4, 5
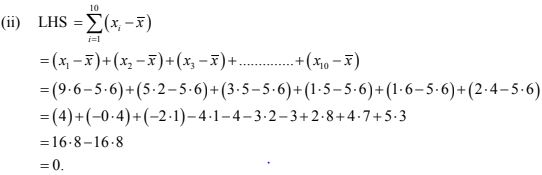
∴ Mean  = Sum of number/Total number 

= (3 + 4 + 5)/3 
= 12/3 = 4

(i) Adding constant term k = 2 in each term

New numbers are = 5, 6, 7.
∴ New mean = (5 + 6 + 7)/3
= 18/3 = 6 = 4 + 2
∴ New mean will be 2 more than the original mean.

(ii) Subtracting constant term k = 2 in each term New number are = 1, 2, 3.
∴ New mean = (1 + 2 +3)/3 = 6/3 = 2 = 4 - 2
∴ New mean will be 2 less than the original mean.

(iii) Multiplying by constant term k = 2 in each term 

New numbers are = 6, 8, 10
New mean = (6 + 8 + 10)/3
= 24/3
= 8
= 4 × 2
∴ New mean will be 2 times of the original mean.

(iv) Divide by constant term k = 2 in each term

New number are = 1.5, 2, 2.5
∴ New mean = (1.5 + 2 + 2.5)/3 
= 6/3 = 2 = 4/2 
∴ New mean will be half of the original mean. 

14. The mean of marks scored by  100 students was found to be  40. Later on it was discovered that a score of 53 was misread as 83. Find the correct mean.

Solution

Mean marks of 100 students = 40 
⇒ Sum of marks of 100 students = 100 × 40 = 4000
Correct value = 53. 
Incorrect value = 83. 
Correct sum = 4000 - 83 + 53 = 3970 
∴ Correct mean = 3970/100 = 39.7

15. The traffic police recorded the speed (in km/hr) of 10 motorists as 47, 53, 49, 60, 39, 42, 55, 57, 52, 48. Later on an error in recording instrument was found. Find the correct average speed of the motorists if the instrument recorded 5 km/hr less in each case.

Solution

The speed of 10 motorists are47,53,49,60,39,42,55,57,52,48

Later on it was discovered that the instrument recorded 5km/hr less than in each case

Corrected values are 52, 58, 54, 65, 44, 47, 60, 62, 57, 53

∴ Correct mean = (52 + 58 + 54 + 65 + 44 + 47 + 60 + 62 + 57 + 53)/10
= 552/10

= 55.2 km/hr

16. The mean of five numbers is 27. If one number is excluded, their mean is 25. Find the

excluded number.

Solution

The mean of the numbers 27 
The, sum of five numbers = 5 × 27 = 135. 
If one number is excluded, then the new mean is 25 
∴ Sum of numbers = 4 × 25 = 100
∴ Excluded number = 135 - 100 = 35

17. The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6

of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.

Solution

The mean weight per student in a group of of 7 students is 55kg.

Weight of 6 students (in kg) = 52, 54, 55, 53, 56 and 54.
Let weight of 7th student  = x kg 

∴ Mean = Sum of all weights/Total students 

⇒ 55 = (52 + 54 + 55 + 53 + 56 + 54 + x)/7 
⇒ 385 = 324 + x 
⇒ x = 385 - 324 
⇒ x = 61 kg 
∴ Weight of 7th student = 61 kg

18. The mean weight of 8 numbers is 15. If each number is multiplied by 2, what will be the new mean?

Solution

We have,

The mean weight of 8 numbers is 15

Then, The sum of 8 numbers = 8 × 15 =120.

If each number is multiplied by 2 

Then, new mean = 120 × 2 = 240 
∴ New mean = 240/8 = 30.

19. The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Find the excluded number.

Solution

The mean of 5 numbers is  18
Then, the sum of 5 numbers = 5 × 18 = 90
If the one number is excluded 

Then, the mean of 4 numbers = 16
∴ Sum of 4 numbers = 4 × 16 = 64 
Excluded number = 90 - 64 = 26

20. The mean of 200 items was  50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean. 

Solution

The mean of 200 items = 50 
Then the sum of  200 items = 200 × 50 = 10000
Correct values = 192  and 88
Incorrect values = 92 = 8
∴ Correct sum = 10000 - 92 - 8 + 192 + 88  = 10180
∴ Correct mean = 10180/200 = 50.9
= 101.8/2 = 50.9

21. Find the values of n and X in each of the following cases:

Solution

22. The sums of the deviations of a set of n values x₁ , x₂ , ... . x₁₁  measured from 15 and −3 are

− 90 and 54 respectively. Find the valùe of n and mean.

Solution

23. Find the sum of the deviations of the variate values 3, 4, 6, 7, 8, 14 from their mean.

Solution

Values are 3, 4, 6, 7, 8, 14.
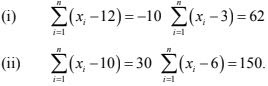
∴ Mean = Sum of numbers/Total number 

= (3 + 4 + 6 + 7 + 8 + 14)/6
= 42/6 = 7
∴ Sum of deviation of values from their mean 

⇒ (3 - 7) + (4 - 7) + (6 - 7) + (7 - 7) + (8 - 7) + (14 - 7) 
⇒ (-4) + (-3) + (-1) + (0) + (1) + (7)
= -8 + 8 = 0

24. If x is the mean of the ten natural numbers x₁ , x₂ , x₃ , ... . x₁₀  , show that, ( x₁ - x ) + (x₂ -  x ) + ....... + (x₁₀ - x ) = 0.

Solution