Chapter 6 Triangles NCERT Exemplar Solutions Exercise 6.4 Class 10 Maths

Chapter Name | NCERT Maths Exemplar Solutions for Chapter 6 Triangles Exercise 6.4 |
Book Name | NCERT Exemplar for Class 10 Maths |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 6.4 Solutions
Long Answer Questions
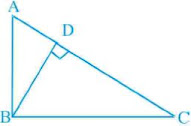
1. In Fig., if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.
Solution
We have,
∠A = ∠C,
AB = 6 cm,
BP = 15 cm,
AP = 12 cm and
CP = 4 cm
In ∆APB and ∆CPD,
∠A = ∠C [given]
∠APB = ∠CPD [vertically opposite angles]
∆APB ~ ∆CPD [by AA similarity criterion]
AP/CP = PB/PD = AB/CD
⇒ 12/4 = 15/PD = 6/CD
So,
12/4 = 15/PD
⇒ PD = 5 cm
Also,
12/4 = 6/CD
⇒ CD = 2 cm
Therefore, length of PD is 5 cm and length of CD is 2 cm.
2. It is given that ∆ ABC ~ ∆ EDF such that AB = 5 cm, AC = 7 cm, DF= 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
Solution
We have,
∆ABC ~ ∆EDF, so the corresponding sides of ∆ABC and ∆EDF are in the same ratio
AB/ED = AC/EF = BC/DF ...(i)
Also, we have,
AB = 5 cm,
AC = 7 cm,
DF= 15 cm and
DE = 12 cm
Putting value in AB/ED = AC/EF = BC/DF ,
5/12 = 7/EF = BC/15
So,
5/12 = 7/EF
⇒ EF = 16.8 cm
Also,
5/12 = BC/15
⇒ BC = 6.25 cm
So, lengths of the remaining sides of the triangles are EF = 16.8 cm and
BC = 6.25 cm.
3. Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Solution
Let us take ∆ABC in which a line DE parallel to BC intersects AB at D and AC at E.
To prove: DE divides the two sides in the same ratio.
AD/DB = AE/EC
Construction :
Join BE and CD
EF ⊥ AB
DG ⊥ AC
Proof :
ar(ADE)/ar(BDE) = (1/2 × AD × EF)/(1/2 × DB × EF)
= AD/DB ...(i)
Also,
ar(ADE)/ar(DEC) = (1/2 × AE × GD)/(1/2 × EC × GD)
= AE/EC ...(ii)
As,
∆BDE and ∆DEC lie between the same parallel lines DE and BC and on the same base DE
So,
ar(∆BDE) = ar(∆DEC) ...(iii)
From Eqs. (i), (ii) and (iii),
AD/DB = AE/EC
Hence proved
4. In Fig., if PQRS is a parallelogram and AB|| PS, then prove that OC || SR.
Solution
We have,
PQRS is a parallelogram, so PQ || SR and PS || QR.
Also,
AB || PS.
To prove :
OC || SR
Proof : In ΔOPS and ΔOAB, PS || AB
∠POS = ∠AOB [common angle]
∠OSP = ∠OBA [corresponding angles]
∆OPS ~ ∆OAB [by AA similarity criterion]
Then PS/AB = OS/OB ...(i)
In ∆CQE and ∆CAB, QR || PS || AB
∠QCR = ∠ACB [common angle]
∠CRQ = ∠CBA [corresponding angles]
So,
∆CQR ~ ∆CAB
QR/AB = CR/OB
PS/AB = CR/OB ...(ii)
(PS = QR, opposite sides of parallelogram)
From (i) and (ii)
OS/OB = CR/CB
or,
OB/OS = CB/CR
Subtracting 1 from both sides, we get,
(OB/OS) - 1 = (CB/CR) - 1
⇒ (OB - OS)/OS = (CB - CR)/CR
⇒ BS/OS = BR/CR
By using converse of basic proportionality theorem, SR || OC.
Hence, proved
5. A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Solution
Taking AC be the ladder of length 5 m and BC = 4 m be the height of the wall, which ladder is placed.
If the foot of the ladder is moved 1.6 m towards the wall so, AD = 1.6 m, then the ladder is slide upward i.e., CE = x m.
In right angled ∆ABC,
AC2 = AB2 + BC2 [Using Pythagoras theorem]
⇒ (5)2 = (AB)2 + (4)2
⇒ AB2 = 25 - 16 = 9
⇒ AB = 3m
Now,
DB = AB - AD
= 3 - 1.6
= 1.4 m
In right angled ∆EBD,
ED2 = EB2 + BD2
[using Pythagoras theorem]
(5)2 = (EB)2 + (1.4)2
[ ∵ BD = 1.4 m]
25 = (EB)2 + 1.96
⇒ (EB)2 = 25 – 1.96 = 23.04
⇒ EB = 4.8
Now,
EC = EB – BC
= 4.8 – 4
= 0.8
Therefore, the top of the ladder would slide upwards on the wall at distance is 0.8 m.
6. For going to a city B from city A, there is a route via city C such that AC⊥CB, AC = 2 x km and CB = 2 (x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
Solution
We have,
AC ⊥ CB,
AC = 2 × km,
CB = 2(x + 7) km and AB = 26 km
On drawing the figure, we get the right angle ∆ACB right angle at C.
Now,
In ∆ACB, by Pythagoras theorem,
AB2 = AC2 + BC2
⇒ (26)2 = (2x)2 + {2(x + 7)}2
⇒ 676 = 4x2 + 4(x2 + 49 + 11x)
⇒ 676 = 4x2 + 4x2 + 196 + 56x
⇒ 676 = 8x2 + 56x + 196
⇒ 8x2 + 56x – 480 = 0
On dividing by 8, we get,
x2 + 7x – 60 = 0
⇒ x2 + 12x-5x-60 = 0
⇒ x(x + 12) – 5(x + 12) = 0
⇒ (x + 12)(x – 5) = 0
⇒ x = -12 or, x = 5
As, distance cannot be negative.
x = 5 [∵ x ≠ 12]
Now,
AC = 2x
= 10 km and
BC = 2(x + 7)
= 2(5 + 7)
= 24 km
The distance covered to reach city B from city A via city C = AC + BC = 10 + 24 = 34 km
Distance covered to reach city B from city A after the construction of the highway is
BA = 26 km
So, the required saved distance is 34 – 26= 8 km.
7. A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Solution
Let BC = 18 m be the flag pole and its shadow be AB = 9.6 m. The distance of the top of the pole, C from the far end which is A of the shadow is AC
In right angled ∆ABC
AC2 = AB2 + BC2 [using Pythagoras theorem]
⇒ AC2 = (9.6)2 + (18)2
⇒ AC2 = 92.16 + 324
⇒ AC2 = 416.16
⇒ AC = 20.4 m
So, the required distance is 20.4 m.
8. A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3m, find how far she is away from the base of the pole.
Solution
Taking A be the position of the street bulb fixed on a pole AB = 6 m and CD = 1.5 m be the height of a woman and her shadow be ED = 3 m. And distance between pole and woman be x m.
In this question, woman and pole both are standing vertically
So,
CD || AB
In ∆CDE and ∆ABE,
∠E = ∠E [common angle]
∠ABE = ∠CDE [each equal to 90°]
∆CDE ~ ∆ABE [by AA similarity criterion]
Then,
ED/EB = CD/AB
⇒ 3/(3 +x) = 1.5/6
⇒ 3×6 = 1.5(3 + x)
⇒ 18 = 1.5 × 3 + 1.5x
⇒ 1.5x = 18 – 4.5
⇒ x = 9 m
So, she is at the distance of 9 m from the base of the pole.
9. In Fig., ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.
Solution
Given,
∆ABC in which ∠B = 90° and
BD ⊥ AC
Also, AD = 4 cm and
CD = 5 cm
In ∆DBA and ∆DCB,
∠ADB = ∠CDB [each equal to 90°]
and
∠BAD = ∠DBC [each equal to 90° – ∠C]
∆DBA ~ ∆DCB [by AA similarity criterion]
So,
DB/DA = DC/DB
⇒ DB2 = DA × DC = 4 × 5
⇒ DB = 2√5 cm
In ΔBDC,
BC2 = BD2 + CD2 (Using Pythagoras theorem)
= (2√5)2 + 52
= 3√5
Also,
ΔDBA ~ ΔDBC
DB/DC = BA/BC
⇒ (2√5)/5 = BA/3√5
⇒ AB = 6 cm
10. 10. In Fig., PQR is a right triangle right angled at Q and QS ⊥ PR . If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
Solution
We have,
In ∆PQR,
∠Q = 90°,
QS ⊥ PR and
PQ = 6 cm,
PS = 4 cm
In ∆SQP and ∆SRQ,
∠PSQ = ∠RSQ [each equal to 90°]
∠SPQ = ∠SQR [each equal to 90° – ∠R]
∆SQP ~ ∆SRQ [By AA similarity criterion]
Then, SQ/PS = SR/SQ
SQ2 = PS × SR
In right angled ΔPSQ,
PQ2 = PS2 + QS2 [using Pythagoras theorem]
⇒ (6)2 = (4)2 + QS2
⇒ 36 = 16 + QS2
⇒ QS2 = 36 – 16 = 20
⇒ QS = 2√5 cm
From eq. (i),
Putting value of PS and QS we get,
RS = 5cm
Now, In QSR,
QR2 = QS2 +SR2
So, putting value of QS and SR we get,
QR = 3√5cm
11. In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a - b) = (c + d)(c - d).
Solution
Given:
In ∆PQR, PD ⊥ QR,
PQ = a,
PR = b,
QD = c and
DR = d
To prove: (a + b)(a -b) = (c + d)(c – d)
Proof:
In right angled ∆PDQ,
PQ2 = PD2 + QD2 [using Pythagoras theorem]
a2 = PD2 + c2
PD2 = a2 - c2 ...(i)
In right angled ∆PDR,
PR2 = PD2 + DR2 [Using Pythagoras theorem]
b2 = PD2 + d2
PD2 = b2 - d2 ...(ii)
From Eq. (i) and (ii)
a2 - c2 = b2 - d2
⇒ a2 - b2 = c2 - d2
⇒ (a - b)(a + b) = (c - d)(c + d)
Hence proved.
12. In a quadrilateral ABCD, ∠A + ∠D = 90° . Prove that AC2 + BD2 = AD2 + BC2
[Hint : Produce AB and DC to meet at E.]
Solution
Given :
Quadrilateral ABCD
∠A + ∠D = 90°
To prove : AC2 + BD2 = AD2 + BC2
Construct : Produce AB and CD to meet at E
Also join AC and BD
Proof:
In ∆AED,
∠A + ∠D = 90° [given]
∠E = 180° – (∠A + ∠D)
= 90° [sum of angles of a triangle = 180°]
So, by Pythagoras theorem,
AD2 = AE2 + DE2
In ∆BEC, by Pythagoras theorem,
BC2 = BE2 + EC2
Adding both equations, we get
AD2 + BC2 = AE2 + DE2 + BE2 + CE2 ...(i)
In ∆AEC, by Pythagoras theorem,
AC2 = AE2 + CE2
In ∆BED, by Pythagoras theorem,
BD2 = BE2 + DE2
Adding both equations, we get
AC2 + BD2 = AE2 + CE2 + BE2 + DE2 ...(ii)
From Eqs. (i) and (ii)
AC2 + BD2 = AD2 + BC2
Hence proved.
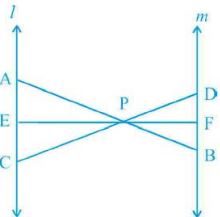
13. In Fig., l || m and line segments AB, CD and EF are concurrent at point P.
Prove that : AE/BF = AC/BD = CE/FD
Solution
We have, l || m and line segment AB, CD and EF are concurrent at point P
To Prove,
AE/BF = AC/BD = CE/FD
In ΔAPC and ΔBPD,
APC = BPD (vertically opposite angles)
PAC =PBD (Alternate angles)
So,
ΔAPC:ΔBPD (By AA Similarity)
AP/PB = AC/BD = PC/PD
Now,
In ΔAPE and ΔBPF,
APE =BPF (vertically opposite angles)
PAE =PBF (Alternate angles)
so,
ΔAPE:ΔBPF (By AA Similarity)
Now,
In ΔPEC and ΔPFD,
APC = BPD (vertically opposite angles)
PAC = PBD (Alternate angles)
so,
ΔPEC:ΔPDF (By AA Similarity)
PC/PD = PE/PF = EC/FD
So, from above equations,
AP/PB = AC/BD = PE/PF = EC/FD = AE/BF
AE/BF = AC/BD = EC/FD
Hence, proved.
14. In Fig., PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
Solution
We have,
AB = 6 cm,
BC = 9 cm,
CD = 12 cm and
SP = 36 cm
Also, PA, QB, RC and SD are all perpendiculars to line l,
PA || QB || RC || SD
Using Basic proportionality theorem,
PQ : QR : RS = AB : BC : CD
= 6 : 9 : 12
Taking,
PQ = 6x,
QR = 9x and
RS = 12x
As,
Length of PS = 36 cm
PQ + QR + RS = 36
⇒ 6x + 9x + 12x = 36
⇒ 27x = 36
⇒ x = 4/3
Now,
PQ = 6x
= 6 × 4/3
= 8 cm
QR = 9x
= 9 × 4/3
= 12 cm
RS = 12x
= 12 × 4/3
= 16 cm
15. O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
Solution
To prove : PO = QO

OP/AD = PD/AD
In ∆ABC and ∆OQC,
OQ || AB
OQ/AB = QC/BC
Also, In ΔADC,
OP || DC
AP/PD = OA/OC
In ΔABC,OQ || AB
BQ/QC = OA/OC
Therefore,
AP/PD = BQ/QC
Adding 1 on both sides,
(AP/PD) + 1 = (BQ/QC) + 1
(AP+ PD)/PD = (BQ + QC)/QC
AD/PD = BC/QC
Or,
PD/AD = QC/BC
Also,
OP/AB = QC/BC and OP/AB = OQ/AB
Therefore,
OP = OQ
[Hint : Take point G on AB such that CG || DF.]


CE = AE ...(i)
Now, in ∆BCG and ∆BDF, CG || DF
BC/CD = BG/GF
⇒ BC/CD = (BF - GF)/GF
⇒ BC/CD = (BF/GF) - 1
⇒ (BC/CD) + 1 = BF/CE [from (ii)]
⇒ (BC + CD)/CD = BF/CE
⇒ BD/CD = BF/CE

AC2 = AB2 + BC2
⇒ AC2 = y2 + x2
⇒ AC = √(y2 + x2 )

A3 = A1 + A2

BC2 = AC2 + AB2
BC2 = y2 + x2
BC = √(y2 + x2 )
Also Area of equilateral triangle = (√3/4)a2
Now we calculate the area A1 , A2 and A3 respectively