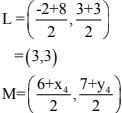Chapter 7 Coordinate Geometry NCERT Exemplar Solutions Exercise 7.1 Class 10 Maths

Chapter Name | NCERT Maths Exemplar Solutions for Chapter 7 Coordinate Geometry Exercise 7.1 |
Book Name | NCERT Exemplar for Class 10 Maths |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 7.1 Solutions
Multiple Choice Questions
Choose the correct answer from the given four options :
1. The distance of the point P (2, 3) from the x-axis is
(A) 2
(B) 3
(C) 1
(D) 5
Solution
(B) 3
We have,
(x, y) is a point on the Cartesian plane in first quadrant.
So,
x = Perpendicular distance from Y – axis and
y = Perpendicular distance from X – axis
Hence, the perpendicular distance from X - axis = y coordinate is 3.
2. The distance between the points A (0, 6) and B (0, –2) is
(A) 6
(B) 8
(C) 4
(D) 2
Solution
(B) 8
We have,
Distance formula : d2 = (x2 – x1)2 + (y2 – y1)2
As given in the question,
x1 = 0,
x2 = 0
y1 = 6,
y2 = – 2
So,
d2 = (0 – 0)2 + ( – 2 – 6)2
⇒ d = √[(0)2 + (-8)2]
⇒ d = √64
⇒ d = 8 units
Hence, the distance between A(0,6) and B(0, 2) is 8.
3. The distance of the point P(-6,8) from the origin is
(A) 8
(B) 2√7
(C) 10
(D) 6
Solution
(C)
Distance formula : d2 = (x2 – x1)2 + (y2 – y1)2
As given in the question,
x1 = -6,
x2 = 0
y1 = 8,
y2 = 0
So,
d2 = [0 – (-6)]2 + [0 – 8]2
⇒ d = √[0 – (-6)]2 + [0 – 8]2
⇒ d = √[(6)2 + (-8)2 ]
⇒ d = √(36 + 64)
⇒ d = √(100)
⇒ d = 10
Hence, the distance between P(-6, 8) and origin O(0, 0) is 10.
4. The distance between the points (0, 5) and (–5, 0) is
(A) 5
(B) 5√2
(C) 2√5
(D) 10
Solution
(B)
Distance formula : d2 = (x2 – x1)2 + (y2 – y1)2
As given in the question,
x1 = 0,
x2 = -5
y1 = 5,
y2 = 0
d2 = [(-5) – 0]2 + [0 – 5]2
⇒ d = √[-5-0]2 + [0 – ]2
⇒ d = √[(-5)2 + (-5)2 ]
⇒ d = √(25+25)
⇒ d = √(50)
⇒ d = 5√2
Hence, the distance between (0, 5) and (-5, 0) = 5√2
5. AOBC is a rectangle whose three vertices are vertices A (0, 3), O (0, 0) and B (5, 0). The length of its diagonal is
(A) 5
(B) 3
(C) √34
(D) 4
Solution
(C)
The three vertices are :
A = (0, 3),
O = (0, 0),
B = (5, 0)
We know that, the diagonals of a rectangle are of equal length,
Length of the diagonal AB = Distance between the points A and B
Distance formula: d2 = (x2 – x1)2 + (y2 – y1)2
As given in the question,
We have;
x1 = 0,
x2 = 5
y1 = 3,
y2 = 0
d2 = [5 – 0]2 + [0 – 3]2
⇒ d = √[5-0]2 + [0 – 3]2
⇒ d = √[(5)2 + (3)2 ]
⇒ d = √(25+9)
⇒ d = √(34)
Distance between A (0, 3) and B(5, 0) is √34.
So, the length of its diagonal is √34.
6. The perimeter of a triangle with vertices (0, 4), (0,0) and (3, 0) is
(A) 5
(B) 12
(C) 11
(D) 7 + √5
Solution
(B) 12
The vertices of a triangle are (0, 4), (0, 0) and (3, 0).
Now, perimeter of ΔAOB = Sum of the length of all its sides :
= distance between (OA + OB + AB)
Distance between the points (x1 , y1) and (x2 , y2) is given by,
d = √[(x2 – x1)2 + (y2 – y1)2 ]
To find :
Distance between A(0, 4) and O(0, 0) + Distance between O(0, 0) and B(3, 0) + Distance between A(0, 4) and B(3, 0).
=√[(0–0)2 + (0–4)2 )+ √ ((3–0)2 + (0–0)2]+ √[(3–0)2 + (0–4)2]
= 12
Hence, the required perimeter of triangle is 12.
7. The area of a triangle with vertices A (3, 0), B(7, 0) and C(8, 4) is
(A) 14
(B) 28
(C) 8
(D) 6
Solution
(C) 8
Vertices of the triangle are,
A(x1 , y1) = (3, 0)
B(x2 , y2) = (7, 0)
C((x3 , y3) = (8, 4)
Area of triangle = 1/2 [x1 (y2 - y3) + x2 (y3 - y1) + x3 ( y1 - y2)]
= 1/2 [3(0 - 4) + 7(4 - 0) + 8(0 - 0)
= 8
Therefore, the area of ΔABC is 8.
8. The points (-4, 0) , (4, 0) , (0, 3) are the vertices of a
(A) right triangle
(B) isosceles triangle
(C) equilateral triangle
(D) scalene triangle
Solution
(B)
Let A(-4, 0), B(4, 0), C(0, 3) are the given vertices.
So, distance between A(-4,0) and B(4, 0),
d2 = [4 – (-4)]2 + [0 – 0]2
⇒ d = 8
Now, distance between B(4, 0) and C(0, 3),
d2 = [0 – (4)]2 + [3 – 0]2
⇒ d = 5
Now, distance between A(-4, 0) and C(0, 3)
d2 = [0 – (-4)]2 + [3 – 0]2
⇒ d = 5
As, BC = AC
ΔABC is an isosceles triangle because an isosceles triangle has two sides equal.
9. The point which divides the line segment joining the points (7, -6) and (3, 4) in ratio 1 : 2 internally lies in the
(A) I quadrant
(B) II quadrant
(C) III quadrant
(D) IV quadrant
Solution
(D) If P (x, y) divides the line segment joining A (x1 , y2 ) and B (x2 , y2 ) internally in the ratio, m : n
It lies in 4th quadrant.
10. The point which lies on the perpendicular bisector of the line segment joining the points A (–2, –5) and B (2, 5) is
(A) (0, 0)
(B) (0, 2)
(C) (2, 0)
(D) (–2, 0)
Solution
x = (-2 + 2)/2
y = (-5 + 5)/2
(x, y) = (0, 0)
So, (0, 0) is the required point lies on the perpendicular bisector of the lines segment.
D = (x4 , y4 )
L, M be the middle points of AC and BD, respectively,
Therefore,
Since, ABCD is a parallelogram, therefore diagonals AC and BD will bisect each other.
Hence, L and M are the same points.
So,
So, the fourth vertex of parallelogram is D = (x4 , y4 )s (0, -1).
12. If the point P (2, 1) lies on the line segment joining points A (4, 2) and B (8, 4),then
(A) AP = (1/3)AB
(B) AP = PB
(C) PB = (1/3)AB
(D) AP = (1/2) AB
Solution
(D)
Given,
The point P(2, 1) lies on the line segment joining the points A(4, 2) and B(8, 5) ,
So,
AB = 2√5
= 2AP
or,
AP = AB/2
So, required condition is AP = AB.
13. If P (a/3 , 4) is the mid - point of the line segment joining the points Q(-6, 5) and R (-2, 3), then the value of a is
(A) - 4
(B) -12
(C) 12
(D) -6
Solution
(B)
Given that, P (a/3 , 4) is the mid - point of the line segment joining the points Q(-6, 5) and R(-2, 3), which shows in the figure,
Midpoint of AB = P
= [(-6-2)/2, (5 + 3)/2]
= (-4, 4)
But midpoint P(a/3, 4) is given,
So,
(a/3, 4) = (-4, 4)
On comparing,
a/3 = -4
⇒ a = -12
so, the required value of a is -12.
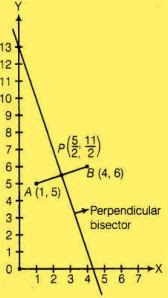
14. The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y - axis at
(A) (0, 13)
(B) (0, -13)
(C) (0, 12)
(D) 13, 0)
Solution
(A)
At first, we plot the points of the line segment on the paper and join them,
We know that, the perpendicular bisector of the line segment AB bisect the segment AB, i.e., perpendicular bisector of line segment AB passes through the mid-point of AB.
Midpoint of (A,B) = P
= [(1 + 4)/2, (5 + 6)/2]
= (5/2, 11/2)
Now, we draw a straight line on paper passes through the mid - point P. We see that the perpendicular bisector cuts the Y - axis at the point (0, 13).
So, the required point is 0, 13).
15. The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the ΔAOB as shown in the fig. is
(A) (x, y)
(B) (x, y)
(C) (x/2, y/2)
(D) y/2 , x/2
Solution
(A)
Let the coordinate of the point which is equidistant from the three vertices O(0, 0), A(0, 2y) and B(2x, 0) is P(h, k).
Then, PO = PA = PB
(PO)2 = (PA)2 = (PB)2
By distance formula,
h2 + k2 = h2 + (k - 2y)2
⇒ 4y(y -k) = 0
⇒ y = k
Taking first and last equations,
h2 + k2 = (h - 2x)2 + k2
⇒ 4x(x - h) = 0
⇒ x = 4
Required points = (h, k)
= (x, y)
16. A circle drawn with origin as the center passes through(13/2, 0). The point which does not lie in the interior of the circle is
(A) -3/4, 1
(B) 2, 7/3
(C) 5, -1/2
(D) -6, 5/2
Solution
(D)
Given,
A circle drawn with origin as the center passes through (13/2, 0)
Radius of the circle = distance between (0, 0) and (13/2 , 0)
= √[(13/2 - 0)2 + (0 - 0)2 ]
= 13/2
= 6.5 (using distance formula)
Now we calculate the distance of each point from the origin.
If the distance is less than 6.5 than the point lies inside the circle otherwise not.
So, point (-6, 5/2) lies on the circle and other point lies inside the circle.
17. A line intersects the y - axis and x - axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(A) (0, – 5) and (2, 0)
(B) (0, 10) and (– 4, 0)
(C) (0, 4) and (– 10, 0)
(D) (0, – 10) and (4, 0)
Solution
(D)
Let the coordinates of P and O(0, y)and (x , 0), respectively .
Now,
Midpoint of PQ is M,
M = (2, -5)
[(0+x)/2, (y + 0)/2] = M
⇒ [(0+x)/2, (y + 0)/2] = (2, -5)
⇒ (0+x)/2 = 2 and
⇒ (y + 0)/2 = -5
On solving,
x = 4
y = -10
so, the coordinates of P and Q are (0, -10) and (4, 0)
18. The area of a triangle with vertices (a, b+c), (b, c + a) and (c, a + b) is
(A) (a + b + c)2
(B) 0
(C) a + b + c
(D) abc
Solution
(B)
Let the vertices of a triangle are,
A = (x1 , y1 )
= (a, b + c)
B = (x2 , y2 )
= (b, c + a) and
C = (x3 , y3 )
= (c, a + b)
Area of ABC = =1/2[x1 (y2 – y3) + x2(y3 – y1) + x3(y1 + y2)
= 1/2 [a (c + a - a - b) + b(a + b - b - c) + c(b + c - c - a)
= (1/2)(0)
= 0
Hence, the required area of triangle is 0.
19. If the distance between the points (4, p) and (1, 0) is 5, then the value of p is
(A) 4 only
(B) ± 4
(C) – 4 only
(D) 0
Solution
(B)
As given in the question,
The distance between the points (4, p) and (1, 0) = 5
Squaring both sides,
9 + p2 = 25
⇒ p2 = 16
⇒ p = ± 4
Hence, the required value of p is ± 4.
20. If the points A((1, 2), O (0, 0) and C (a, b) are collinear, then
(A) a = b
(B) a = 2b
(C) 2a = b
(D) a = -b
Solution
(C)
Let the given points are
A = (x1 , y1 )
= (1, 2)
B = (x2 , y2 )
= (0, 0)
C = (x3 , y3 )
= (a, b)
Area of ABC = 1/2[x1 (y2 - y3 ) + x2 (y3 - y1 ) + x3 (y1 + y2 )
= (1/2) [1(0 - b) + 0(b - 2) + a(2 + 0)]
= (1/2) [2a - b)
As the points are collinear,
ar(ABC) = 0
(1/2)(2a - b) = 0
2a = b
So, 2a = b is required relation,
Hence, the required relation is 2a = b.