NCERT Exemplar Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.3

Chapter 6 Triangles NCERT Exemplar Solutions Exercise 6.3 Class 10 Maths

Chapter Name	NCERT Maths Exemplar Solutions for Chapter 6 Triangles Exercise 6.3
Book Name	NCERT Exemplar for Class 10 Maths
Other Exercises	Exercise 6.1 Exercise 6.2 Exercise 6.4
Related Study	NCERT Solutions for Class 10 Maths

Exercise 6.3 Solutions

Short Answer Questions

1. In a ΔPQR, PR² - PQ² = QR² and M is a point on side PR such that QM ⊥ PR. 
Prove that : 
QM² = PM × MR.

Solution

In ∆PQR,
PR² = QR² and 
QM ⊥ PR

Using Pythagoras theorem, we have, 
PR² = PQ² + QR² 
∆PQR is right angled triangle at Q. 
From ∆QMR and ∆PMQ, we get,
∠M = ∠M
∠MQR = ∠QPM [each 90°-∠R]
So, using the AAA similarity criteria,
We have,
∆QMR ∼ ∆PMQ
Also,
Area of triangles = 1/2 × base  × height 
So, by property of area of similar triangles, 

QM² = PM  × RM 
Hence proved.

2. Find the value of x for which DE || AB in given figure. 

Solution

As given in the question, 
DE || AB 
Using basic proportionality theorem, 
CD/AD = CE/BE
If a line is drawn parallel to one side of a triangle such that it intersects the other sides at distinct points, then, the other two sides are divided in the same ratio. Therefore, we can conclude that, the line drawn is equal to the third side of the triangle.
(x +3)/(3x + 19) = x/(3x + 4) 
⇒ (x + 3)(3x + 4) = x(3x + 19) 
⇒ 3x² + 4x + 9x + 12 = 3x² + 19x 
⇒ 19x - 13x = 12 
⇒ 6x = 12 
⇒ x = 2 

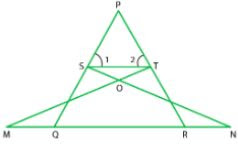
3. In figure, if ∠1 =∠2 and ∆ NSQ ≅ ∆MTR, then prove that ΔPTS ~ ΔPRQ.

Solution

As given in the question, 
ΔNSQ ≅ ΔMTR
∠1 = ∠2
As,
∆NSQ = ∆MTR
So,
SQ = TR ...(i)
Also,
∠1 = ∠2
So,
PT = PS ...(ii)
[As, sides opposite to equal angles are also equal]
Using Equation (i) and (ii).
PS/SQ = PT/TR
So,
ST || QR
By converse of basic proportionality theorem, If a line is drawn parallel to one side of a triangle to intersect the other sides in distinct points, the other two sides are divided in the same ratio.
∠1 = PQR and∠2 = ∠PRQ
Now, In ∆PTS and ∆PRQ.
∠P = ∠P   [Common angles]
∠1 = ∠PQR  (proved)
∠2 = ∠PRQ   (proved)
∆PTS – ∆PRQ  [By AAA similarity criteria]
Hence proved.

4. Diagonals of a trapezium PQRS intersect each other at the point 0, PQ || RS and PQ = 3 RS. Find the ratio of the areas of Δ POQ and Δ ROS.

Solution

As given in the question, 
PQRS is a trapezium in which PQ || RS and PQ = 3RS 
PQ/RS = 3/2  ...(i) 

In ∆POQ and ∆ROS,
∠SOR = ∠QOP  [vertically opposite angles]
∠SRP = ∠RPQ   [alternate angles]
∆POQ ∼ ∆ROS  [by AAA similarity criterion]
Using property of area of similar triangle,

So, the required ratio  = 9 : 1.

5. In figure, if AB || DC and AC, PQ intersect each other at the point O. Prove that OA.CQ = OC.AP.

Solution

As given in the question,
AC and PQ intersect each other at the point O and AB||DC.
Using ∆AOP and ∆COQ,
∠AOP = ∠COQ   [as they are vertically opposite angles]
∠APO = ∠CQO   [since, AB||DC and PQ is transversal, Angles are alternate angles]
So,
∆AOP ∼ ∆COQ  [using AAA similarity criterion]
As, corresponding sides are proportional
We have,
OA/OC = AP/CQ 
OA × CQ = OC × AP 
Hence, Proved.

6. Find the altitude of an equilateral triangle of side 8 cm.

Solution

Taking ABC be an equilateral triangle of side 8 cm. 

AB = BC = CA = 8 cm   (sides of an equilateral triangle is equal)

Draw altitude AD which is perpendicular to BC.

Then, D is the mid-point of BC.

BD = CD = 1/2

BC = 8/2 = 4 cm

Now,

Using Pythagoras theorem

AB² = AD² + BD² 
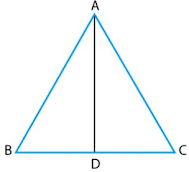
⇒ (8)² = AD² + (4)² 
⇒ 64 = AD² + 16 
⇒ AD = √48
⇒ AD = 4√3 cm. 

Therefore, altitude of an equilateral triangle is 4√3cm.

7. If ∆ABC ∼ ∆DEF, AB = 4 cm, DE = 6, EF = 9 cm and FD = 12 cm, then find the perimeter of ∆ABC.

Solution

As given in the question,

AB = 4 cm,

DE = 6 cm

EF = 9 cm

FD = 12 cm

Also,

∆ABC ∼ ∆DEF

We have,
AB/ED = BC/EF = AC/DF
4/6 = BC/9 = AC/12 
Now, 4/6 = BC/9 
BC = 6 cm
Similarly, 
AC/12 = 4/6 
⇒ AD AC = 8cm 
Perimeter of ∆ABC = AB + BC + AC 
= 4 + 6 + 8 = 18 cm 
So, the perimeter of the triangle is 18 cm. 

8. In Fig. 6.11, if DE || BC, find the ratio of ar(ADE) and ar(DECB) .

Solution

We have, 
DE || BC,  
DE = 6 cm and 
BC = 12 cm 
In ΔABC and ΔADE, 
∠ABC = ∠ADE   [corresponding angle]
and 
∠A = ∠A  [common side]

∆ABC ~ ∆ADE  [using AA similarity criterion]

ar(ADE)/ar(ABC) = DE² /BC² 
= 6² /12²  = 1/4 
Taking, 
ar(∆ADE) = k, then 
⇒ ar(∆ABC) = 4k
Now, 
ar(∆ECB) = ar(ABC) - ar(ADE) 
= 4k - k = 3k 
So, 
Required ratio  = ar(ADE) : ar(DECB)
= k : 3k 
= 1 : 3

9. ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm , find AD.

Solution

We have , a trapezium ABCD in which AB || DC.  P and Q are points on AD and BC, respectively such that PQ || DC.
So, AB || PQ || DC. 

In ∆ABD,
PO || AB
DP/AP = DO/OB  ...(i)

In ∆BDC,
OQ || DC
BQ/QC = OB/OD
or, QC/BQ = DO/OB  ...(ii)
So, from (i) and (ii),
DP/AP = QC/BQ
⇒ 18/AP = 15/35
AP = 42 cm
Also,
AD = AP + PD
= 42 + 18 = 60
So, AD = 60 cm

10. Corresponding sides of two similar triangles are in the ratio of 2:3. If the area of the smaller triangle is 48 cm², find the area of the larger triangle.

Solution

According to the question,

Ratio of corresponding sides of two similar triangles is 2 : 3 or 2/3

Area of smaller triangle = 48 cm² 

Using the property of area of two similar triangles,

Ratio of area of both triangles = (Ratio of their corresponding sides)² 

ar(smaller triangle)/ar(larger triangle) = (2/3)² 

⇒ 48/ar(larger triangle) = (2/3)² 

⇒ ar(larger triangle) 108cm² 

11. In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN.NR = QN², prove that ∠PQR = 90°.

Solution

We have, 
In ΔPQR, N is a point on PR, such that QN ⊥ PR and PN .

NR = QN² 

To prove: ∠PQR = 90°

Proof:

We have, PN.NR = QN² 

PN.NR = QN.QN

So,

PN/QN = QN/NR 

Also, 

∠PNQ = ∠RNQ  [each equal to 90°]

∆QNP ~ ∆RNQ   [by SAS similarity criterion]

So we can say, ∆QNP and ∆RNQ are equiangular.

∠PQN = ∠QRN

∠RQN = ∠QPN

On adding both sides,

∠PQN + ∠RQN = ∠QRN + ∠QPN

∠PQR = ∠QRN + ∠QPN  ...(ii)

We have, sum of angles of a triangle is 180°

In ∆PQR,

∠PQR + ∠QPR + ∠QRP = 180°

⇒ ∠PQR + ∠QPN + ∠QRN = 180°  [ ∵∠QPR = ∠QPN and ∠QRP = ∠QRN]

∠PQR + ∠PQR = 180°  [using Eq. (ii)]

⇒ 2∠PQR = 180°

⇒ ∠PQR = 90°

Hence proved.

12. Areas of two similar triangles are  36 cm²  and 100 cm²  . If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.

Solution

We have,

Area of smaller triangle = 36 cm²  

Area of larger triangle = 100 cm²  

And, length of a side of the larger triangle = 20 cm

Let length of the corresponding side of the smaller triangle = x cm

By property of area of similar triangles,

ar(larger triangle)/ar(smaller triangle) = (side of larger triangle)²/(side of smaller triangle)²  

⇒ 100/36 = 20²/x²  
⇒ x = 12 cm 

13. In the given fig., if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD. 

Solution

We have,

AC = 8 cm,

AD = 3 cm

∠ACB = ∠CDA

In ∆ACD and ∆ABC,

∠A = ∠A  [Common angle]

∠ADC = ∠ACB  [Given]

So,

∆ADC ~ ∆ACB  [By AA similarity criterion]
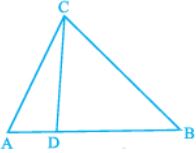
AC/AD = AB/AC
⇒ 8/3 = AB/8 
⇒ AB = 64/3 cm 
Also, 
AB = BD + AD 
⇒ 64/3 = BD + 3 
⇒ BD = 55/3 cm 

14. A 15 meters high tower casts a shadow 24 meters long at a certain time and at the same time, a telephone pole casts a shadow 16 meters long. Find the height of the telephone pole.

Solution

Taking BC = 15 m be the tower and its shadow AB is 24 m.

Let ∠CAB = θ.

Again, let EF = h be a telephone pole and its shadow DE = 16 m.

At the same time ∠EDF = θ.

∆ABC and ∆DEF both are right angled triangles.

In ∆ABC and ∆DEF

∠CAB = ∠EDF

∠B = ∠E
So by AA rule, 

∆ABC～∆DEF
AB/DE = BC/EF
⇒ 24/16 = 15/h
⇒ h = 10 
Hence, the height of the point on he wall where the top of the ladder reaches is 8 m. 

15. Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.

Solution

Let AB be a vertical wall and AC = 10 m is a ladder.

The top of the ladder reached to A and distance of ladder from the base of the wall BC is 6 m.
In right angled ∆ABC 
AC²  = AB²  + BC²  
⇒ (10)²  = AB²  + (6)²  
⇒ 100 = AB²  + 36 
⇒ AB²  = 100 - 36 = 64 
⇒ AB = 8 m 
Therefore, the height of the point on the wall where the top of  the ladder reaches is 8 m.