RD Sharma Solutions for Class 10 Chapter 7 Statistics Exercise 7.4

RD Sharma Solutions Chapter 7 Statistics Exercise 7.4 Class 10 Maths

Chapter Name	RD Sharma Chapter 7 Statistics
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 7.1 Exercise 7.2 Exercise 7.3 Exercise 7.5 Exercise 7.6
Related Study	NCERT Solutions for Class 10 Maths

Exercise 7.4 Solutions

1. Following are the lives in hours of 15 pieces of the components of aircraft engine. find the median:

715,724,,725,710,729,745,694,699,696,712,734,728,716,705,719.

Solution

Lives in hours of is pieces are 
= 715, 724, 725, 710, 729, 745, 694, 699, 696, 712,734,728,719,705,705,719
Arrange the above data in a sending order
694,696,699,705,710,712,715,716,719,721,725,728,729,734,745
N = 15(odd) 

2. The following is the distribution of height of students of a certain class in a certain city.

Height (in cm):	160 – 162	163 – 165	166 – 168	169 – 171	172 – 174
No. of students:	15	118	142	127	18

Find the median height.

Solution

3. Following is the distribution of I.Q. of loo students. Find the median I.Q.

I.Q.:	55 – 64	65 – 74	75 – 84	85 – 94	95 – 104	105 – 114	115 – 124	125 – 134	135 – 144
No. of Students:	1	2	9	22	33	22	8	2	1

Solution

4. Calculate the median from the following data:

Rent (in Rs.):	15 – 25	25 – 35	35 – 45	45 – 55	55 – 65	65 – 75	75 – 85	85 – 95
No. of houses:	8	10	15	25	40	20	15	7

Solution

5. Calculate the median from the following data:

Marks below:	10	20	30	40	50	60	70	80
No. of students:	15	35	60	84	96	127	198	250

Solution

6. An incomplete distribution is given as follows:

Variable:	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70
Frequency:	10	20	?	40	?	25	15

Solution

7. Calculate the missing frequency from the following distribution, it being given that the median of the distribution is 24.

Age in years:	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
No. of persons:	5	25	?	18	7

Solution

8. Find the missing frequencies and the median for the following distribution if the mean is 1.46.

No. of accidents:	0	1	2	3	4	5	Total
Frequency (No. of days):	46	?	?	25	10	5	200

Solution

9. An incomplete distribution is given below:

Variable:	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70	70 – 80
Frequency:	12	30	-	65	-	25	18

You are given that the median value is 46 and the total number of items is 230.
(i) Using the median formula fill up missing frequencies.
(ii) Calculate the AM of the completed distribution.

Solution

10. The following table gives the frequency distribution of married women by age at marriege:

Age(in years)	Frequency	Age(in years)	Frequency
15 – 19	53	40 – 44	9
20 – 24	140	45 – 49	5
25 – 29	98	50 – 54	3
30 – 34	32	55 – 59	3
35 – 39	12	60 and above	2

Calculate the median and interpret the results

Solution

11. If the median of the following frequency distribution is 28.5 find the missing frequencies:

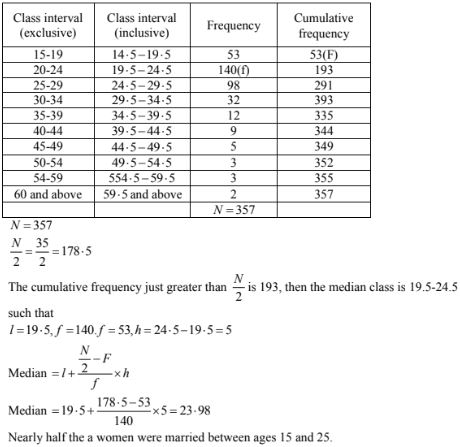
Class interval:	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	Total
Frequency:	5	F1	20	15	F2	5	60

Solution

12. The median of the following data is 525. Find the missing frequency, if it is given that there are 100 observations in the data:

Class interval	Frequency	Class interval	Frequency
0 – 100	2	500 – 600	20
100 – 200	5	600 – 700	F2
200 – 300	F1	700 – 800	9
300 – 400	12	800 – 900	7
400 – 500	17	900 – 1000	4

Solution

13. If the median of the following data is 32.5, find the missing frequencies.

Class interval:	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70	Total
Frequency:	F1	5	9	12	F2	3	2	40

Solution

14. A survey regarding the height(in cm) of 51 girls of X of a school was conducted and the following data was obtained:

(i) Marks	No. of students	(ii) Marks	No. of students
Less than 10	0	More than 150	0
Less than 30	10	More than 140	12
Less than 50	25	More than 130	27
Less than 70	43	More than 120	60
Less than 90	65	More than 110	105
Less than 110	87	More than 100	124
Less than 130	96	More than 90	141
Less than 150	100	More than 80	150

Solution

15. A survey regarding the height(in cm) of 51 girls of class X of a school was conducted and the following data was obtained:

Height in cm	Number of Girls
Less than 140	4
Less than 145	11
Less than 150	29
Less than 155	40
Less than 160	46
Less than 165	51

Find the median height.

Solution

To calculate the median height, we need to find the class intervals and their corresponding frequencies
The given distribution being of thee less than type 140, 145, 150,  ........, 165 give the upper limits of corresponding class intervals. So, the classes should be below 140 , 145, 150, .....160, 165  observe that from the given distribution , we find that there are 4 - girls with height less than 140 is 4. Now there are 4 girls with heights less than 140. Therefore, the number of girls with height in the interval 140, 145 is 11 - 4 = 7, similarly. The frequencies of 145, 150 is 29 - 11 = 18, for 150 - 155 it is 40 -29 =11, and so on so our frequencies distribution becomes. 

16. A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are only given to persons having age 18 years onwards but less than 60 years.

Age in years	Number of policy holders
Below 20	2
Below 25	6
Below 30	24
Below 35	45
Below 40	78
Bwlow 45	89
Below 50	90
Below 55	98
Below 60	100

Solution

Here class width is not same. There is no need to adjust the frequencies according to class intervals. Now given frequencies table is of less than type represented with upper class limits. As policies were given only to persons having age 18 years onwards but less than 60 years we can definite class intervals with their respective cumulative frequencies as below

17. The lengths of 40 leaves of a plant are measured correct to the nearest millimeter, and the data obtained is represented in the following table:

Length( in mm):	118 – 126	127 – 135	136 – 144	145 – 153	154 – 162	163 – 171	172 – 180
No.of leaves:	3	5	9	12	5	4	2

Find the mean length of life.

Solution

The given data is not having continuous class intervals is 1. So, we have to add and subtract 1/2 = 0.5. upper class limits and lower class limits
Now continuous class intervals with respective cumulative frequencies can be presented as below

18. The following table gives the distribution of the life time fo 400 neon lamps:

Lite time(in hours)	Number of lamps (1500 – 2000) 14
2000 – 2500	56
2500 – 3000	60
3000 – 3500	86
3500 – 4000	74
4000 – 4500	62
4500 – 5000	48

Find the median life.

Solution

We can find cumulative frequencies with their respective class intervals as below

19. The distribution below gives the weight of 30 students in a class. Find the median weight f students:

Weight (in kg):	40 – 45	45 – 50	50 – 55	55 – 60	60 – 65	65 – 70	70 – 75
No. of students	2	3	8	6	6	3	2

Solution