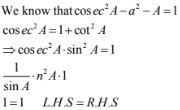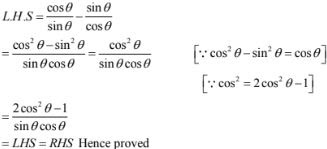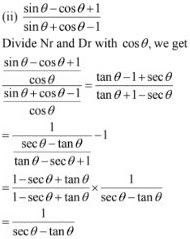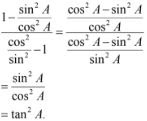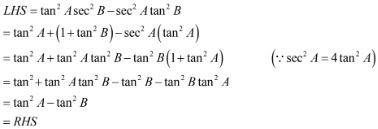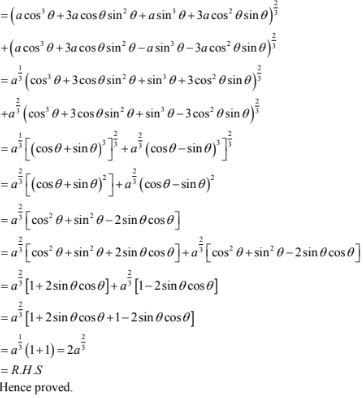RD Sharma Solutions Chapter 6 Trigonometric Identities Exercise 6.1 Class 10 Maths
Chapter Name | RD Sharma Chapter 6 Trigonometric Identities |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises | |
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 6.1 Solutions
Prove the following trigonometric identities :
1. ( 1 – cos2 A) cosec2 A = 1
Solution
2. (1 + cos2 A)sin2 A = 1 Solution
3. tan2 θ cos2 θ = 1 - cos2 θ
Solution
4. cosec θ √(1 - cos2 θ) = 1
Solution

5. (sec2 θ - 1)(cosec2 θ - 1) = 1
Solution
We know that sec2 θ - tan2 θ = 1
⇒ sec2 θ = 1, tan θ
cosec2 θ - cos2 θ = 1
cosec2 θ - cot2 θ
tan2 θ .cot2 θ = tan2 θ(1/tan2 θ)
6. tanθ(1/tanθ) = secθ cosecθ
Solution
7. cosθ/(1 - sinθ) = (1 + sinθ)/cos θ
Solution
8. cos θ/(1 + sinθ) = (1 - sin θ)/cos θ
Solution
9. cos2 A + 1/(1 + cot2 A) = 1
Solution
1 + cot2 A = cosec2 A [∵ cosec2 A - cot2 A = 1, cosec2 A = 1 + cot2 A]
⇒ cot2 A + 1/cosec2 A
⇒ cos2 A + sin2 A = 1
∴ LHS = RHS
10. sin2 A + 1/(1 + tan2 A) = 1
Solution
1 + tan2 A = sec2 A [∵ sec2 A - tan2 A = 1]
⇒ sin2 A + 1/sec2 A [1 + tan2 A - sec2 A]
⇒ sin2 A + cos2 A = 1
∴ LHS = RHS
11. √(1 - cos θ)/(1 + cos θ) = cosec θ - cot θ.
Solution
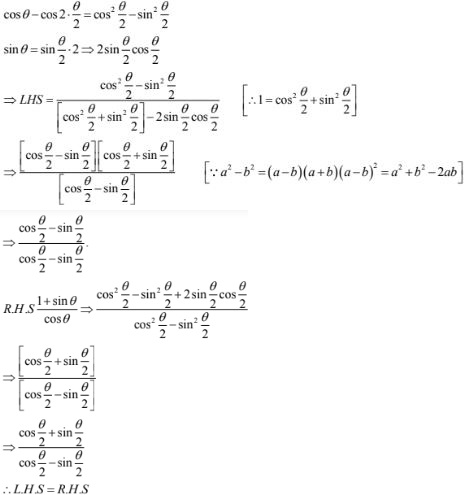
12. (1 - cosθ)/sinθ = sinθ/(1 + cosθ)
Solution
13. sin θ/(1 - cos θ) - cosec θ + cot θ
Solution
14. (1 - sin θ)/(1 + sin θ) - (sec θ - tan θ)2
Solution
15. (cosec θ + sin θ)(cosec θ - sin θ) = cos2 θ
Solution
16. (1 + cot2 θ)tanθ/sec2 θ = cot θ
Solution
17. (sec θ + cos θ)(sec θ - cos θ) = tan2 θ + sin2 θ
Solution
18. sec A(1 - sin A)(sec A + tan A) = 1
Solution
19. (cosec A - sin A)(sec A - cos A)(tan A + cot A) = 1
Solution
20. tan2 θ - sin2 θ = tan2 θ .sin2 θ
Solution
21. (1 + tan2 θ)(1 - sin θ).(1 + sin θ) = 1
Solution

= 1
= LHS = RHS Hence proved
22. sin2 A cot2 A + cos2 A tan2 A = 1
Solution
23. (i) cos θ - tan θ = (2cos2 θ - 1)/(sin θ cos θ)
Solution
(ii) tan θ - cot θ = (2 sin2 θ - 1)/(sin θ cos θ)
Solution
24. cos2 θ/sin θ - cosec θ + sin θ = θ
Solution
25. 1/(1+sinA) + 1/(1 - sinA) = 2sec2 A
Solution
26. (1 + sin θ)/cos θ + cos A/(1 + sin θ) = 2 sec θ
Solution
27. ([1 + sin θ)2 + (1 - sin θ)2 ]/2 cos2 θ = (1 + sin2 θ)/(1 - sin2 θ)
Solution
28. (1 + tan2 θ)/(1 + cot2 θ) - [(1 - tan θ)/cotθ]2 - tan2 θ
Solution
29. (1 + sec θ)/sec θ = sin2 θ/(1 - cosθ)
Solution
30. tan θ/(1- cotθ) = cotθ/(1 - tan θ) = 1 + tan θ + cot θ.
Solution
31. sec6θ = tan6θ + 3tan2 θ sec2 θ + 1
Solution
We know that sec2 θ - tan2 θ :
Cubing on both sides
(sec2 θ - tan2 θ)3 = 1
sec6 θ - tan6 θ - 3sec2 θ.tan2 θ(sec2 θ - tan2 θ) = 1
[∵(a - b)3 = a3 - b3 - 3ab(a - b)]
⇒ sec6 θ - tan6 θ = 3sec2 θ.tan2 θ = 1
⇒ sec6 θ = tan6 θ+ 3sec2 θ.tan2 θ + 1
Hence, proved.
32. cosec6 θ = cot6 θ+ 3cot2 θ cosec2 θ + 1
Solution
We know that cosec2 θ - cot2 θ = 1
Cubing on both sides
(cosec2 θ - cot2 θ)3 = (1)3

33. (1+ tan2 θ)cot θ/ cosec2 θ = tan θSolution
34. (1 + cos A)/sin2 A = 1/(1 - cos A)
Solution
We know that sin2 A + cos2 A = 1
Sin2 A = 1 - cos2 A
⇒ sin2 A = (1 - cos A)(1 + cos A)
35. (sec A - tan A)/(sec A + tan A) = cos2 A/(1 + sin A)2
Solution
LHS = (sec θ - tan θ)/(sec A + tan A)
Rationalizing the denominator, multiply and diving with sec A + tan A we get
36. (1 + cos A)/sin A = sin A/(1 - cos A)Solution
37. √(1 + sin A)/(1 - sin A) = sin A + tan A
Solution
38. √(1 - cos A)/(1 + cos A) = cosec A - cot A
Solution
39. (sec A - tan A)2 = (1 - sin A)/(1 + sin A)
Solution
40. (1 - cos A)/(1 + cos A) = (cot A - cosec A)2
Solution
41. 1/(sec A - 1) + 1/(sec A + 1) = 2cosec A. cot A
Solution
42. cos A/(1 - tan A) + sin A/(1 - cot A) = sin A + cos ASolution
43. cosec A/(cosec A - 1) + cosec A/(cosec A + 1) = 2sec2 A.
Solution
44. (1 + tan2 A) + (1 + 1/tan2 A) = 1/(sin2 A - sin4 A)
Solution
45. tan2 A/(1 + tan2 A) + cot2 A/(1 + cot2 A) = 1
Solution
46. (cot A - cos A)/(cos A + cos A) = (cosec A - 1)/(cosec A + 1)
Solution
47. (i) (1 + cos θ + sin θ)/(1 + cos θ - sin θ)
(ii) (sin θ - cosθ + 1)/(sin θ + cos θ - 1)
(iii) (cos θ - sin θ + 1)/(cos θ + sin θ - 1) = cosec θ + cot θ
Solution
(i) (1 + cos θ + sin θ)/(1 + cos θ - sin θ)
(ii) (sin θ - cosθ + 1)/(sin θ + cos θ - 1)
(iii) (cos θ - sin θ + 1)/(cos θ + sin θ - 1) = cosec θ + cot θ
Solution
49. tan2 A + cot2 A = sec2 A cosec2 A - 2
Solution
50. (1 - tan2 A)/(cot2 A- 1) = tan2 A.
Solution
51. 1 + cot2 θ/(1 + cosec θ) = cosec θ
Solution
52. cos θ/(cosecθ + 1) + cos θ/(cosec θ -1) = 2 tan θ
Solution
53. (1 + cos θ - sin2 θ)/[sin θ(1 + cos θ)] = cot θ
Solution
54. tan3 θ/(1 + tan2 θ) + cot3 θ/(1 + cot2 θ) = sec θ cosec θ - 2sin θ cos θ
Solution
55. If Tn = sinn θ + cosn θ, prove that (T3 – T5 )/T1 = (T5 – T7)/T3Solution
56. [tan θ + 1/cos θ]2 + [tan θ - 1/cos θ]2 = 2[(1 + sin2 θ)/(1 - sin2 θ)
Solution
57. [1/(sec2 θ – cos2 θ) + 1/(cosec2 θ – sin2 θ)]sin2 θcos2 θ = (1 – sin2 θcos2 θ)/(2 + sin2 θcos2 θ)
Solution
58. [(1 + sin θ - cos θ)/(1 + sin θ + cos θ)]2 = (1 - cos θ)/(1 + cos θ)
Solution
59. (sec A + tan A - 1)(sec A - tan A + 1) = 2tan A
Solution
60. (1 + cot A - cosec A)(1 + tan A + sec A) = 2
Solution
61. (cosec θ - sec θ)(cot θ - tan θ)(cosec θ + sec θ)(sec θ cosec θ - 2)
Solution
62. (sec A - cosec A)(1 + tan A + cot A) = tan A sec A - cot A cosec A
Solution
63. (cos A cosec A - sin A sec A)/(cos A + sin A) = cosec A - sec A Solution
64. sin A/(sec A + tan A -1) + cot A/(cosec A + cot A - 1) = 1
Solution
65. tan A/(1 + tan2 A) + cos A/(1 + cot2 A)2 = sin A cos A
Solution
66. sec4 A(1 - sin4 A) - 2 tan4 A = 1
Solution
67. cot2 A(sec A - 1)/(1 + sin A) = sec2 [(1 - sin A)/(1 + sec A)]
Solution
68. (1 + cot A + tan A)(sin A - cos A) = sec A/(cosec2 A) - cosec A/sec2 A = sin A tan A - cos A cot A
Solution
69. sin2 A cos2 B - cos2 A sin2 B = sin2 A - sin2 B
Solution
70. (cot A + tan B)/(cot B + tan A) = cot A tan B
Solution
71. (tan A + tan B)/(cot A + cot B) = tan A tan B
Solution
72. cot2 A cosec2 B - cot2 B cosec2 A = cot2 A - cot2 B
Solution
73. tan2 A sec2 B - sec2 A tan2 B = tan2 A - tan2 B
Solution
74. If x = a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x2 - y2 = a2 - b2
Solution
75. If x/a cos θ + y/b sin θ = 1 and x/a sin θ - y/b cos θ = 1, prove that x2/a2 + y2/ b2 = 2
Solution
76. If cosec θ - sin θ = a2 , sec θ - cos θ = b3 , prove that a2b2(a2 + b2 ) = 1
Solution
77. If a cos3 θ + 3α cos θ sin2 θ = m, α sin3 θ + 3α cos2 θ sin θ = n, prove that (m + n)2/3 + (m -n)2/3
Solution
78. If x = a cos3 θ, y = b sin3 θ, prove that (x/a)2/3 θ + (y/b)2/3 = 1
Solution
79. If 3 sin θ + 5 cos θ = 5, prove that 5 sin θ - 3 cos θ = ±3.
Solution
80. If a cos θ + b sin θ = m and a sin θ - b cos θ = n, prove that a2 + b2 = m2 + n2
Solution
81. If cos θ + cot θ = m and cosec θ - cot θ = n, prove that m n = 1
Solution
82. If cos A + cos2 A = 1 , prove that sin2 A + sin4 A = 1
Solution
cos A + cos2 A = 1
cos A = 1 - cos2 A
cos A = sin2 A
LHS = sin2 A + sin4 A
= sin2 A+ sin2 A
= sin2 A + (cos A)2
= sin2 A + cos A
= 1
83. Prove that :
(i) √(sec θ - 1)/(sec θ + 1) + √(sec θ + 1)/(sec θ - 1) = 2 cosec θ
(ii) √(1 + sin θ )/(1 - sin θ) + √(1 - sin θ)/(1 + sin θ) = 2 sec θ
(iii) √(1 + cos θ )/(1 - cos θ) + √(1 - cos θ)/(1 + cos θ) = 2 cosec θ(iv) (sec θ - 1)/(sec θ + 1) = (sinθ/(1 + cos θ))2
Solution
(i) √(sec θ - 1)/(sec θ + 1) + √(sec θ + 1)/(sec θ - 1) = 2 cosec θ
(ii) √(1 + sin θ )/(1 - sin θ) + √(1 - sin θ)/(1 + sin θ) = 2 sec θ
(iii) √(1 + cos θ )/(1 - cos θ) + √(1 - cos θ)/(1 + cos θ) = 2 cosec θ
(iv) (sec θ - 1)/(sec θ + 1) = (sinθ/(1 + cos θ))2
84. If cos θ + cos2 θ = 1, prove that
sin12 θ + 3sin10 θ + 3sin8 θ + sin6 θ + 2 sin4 θ + 2sin2 θ - 2 = 1 Solution
85. Given that (1 + cos α)(1 + cos β)(1 + cosγ) = (1 - cos α)(1 - cos β)(1 - cos γ)
Show that one of the values of each member of this equality is sin α sin β sin γ
Solution
86. If sin θ + cos θ = x P.T sin6 θ + cos6 θ = [4 - 3(x2 - 1)2 /4]
Solution
87. if x = a sec θ cos ∅y = b sec θ sin∅ and z = c tan θ, S.T x2/a2 + y2/b2 - z2/c2 = 1
Solution