RD Sharma Solutions for Class 10 Chapter 5 Trigonometric Ratios Exercise 5.3

RD Sharma Solutions Chapter 5 Trigonometric Ratios Exercise 5.3 Class 10 Maths

Chapter Name	RD Sharma Chapter 5 Trigonometric Ratios
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 5.1 Exercise 5.2
Related Study	NCERT Solutions for Class 10 Maths

Exercise 5.3 Solutions

Evaluate the following : 

1. sin 20°/cos 70°

Solution 

(ii) cos19°/sin71°

Solution 

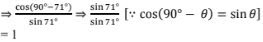
(iii) sin 21°/cos 69° 

Solution 

(iv) tan 10°/cot 80° 

Solution 

(v) sec 11°/cosec 79° 

Solution 

Evaluate the following : 

2. (i) [sin 49°/cos 45°]² + [cos 41°/sin 49°]

Solution 

(ii) cos 48° - sin 42°

Solution 

cos 48° = cos(90° - 42°) sin 42°
∴ sin 42° - sin 42° = 0 

(iii) cot 40°/cos 35° - 1/2[ cos 35°/sin 55°]

Solution

(iv) [sin 27°/cos 63°] - [cos 63°/sin 27°]² 

Solution

(v) tan 35°/ cot 55° + cot 63°/cos 63° - 1 

Solution

(vi) sec 70°/cosec 20° + sin 59°/cos 31°

Solution

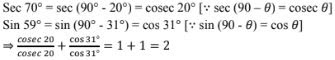
(vii) sec 50° sin 40° + cos 40° cosec 50°

Solution

sec 50° = sec (90° - 40°) = cosec 40°
cos 40° = cos(90° - 50°) = sin 50°
∴ sin θ cosec θ = 1 
⇒ cosec 40° sin 40° + sin 50° cosec 50° 
⇒ 1+ 1  = 2

3. Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
(i) sin 59° + cos 56°

Solution 

sin 59° = sin (90° - 59°) = cos 31°
cos 56° = cos (65° - 34°) = sin 34° 
⇒ cos 31° + sin 34°

(ii) tan 65° + cot 49° 

Solution

tan 65° = tan(90° - 25°) = cot 5°
cot 49° = cot(90° - 41°) = tan 41°
⇒ cot 25° + tan 41°

(iii) sec 76° + cosec 52°

Solution

sec 76° = sec(90° - 14°) = cosec 14°
cosec 52° = cosec(90° - 88°) = sec 38°
⇒ cosec 14° + sec 38°

(iv) cos 78° + sec 78°

Solution

cos 78° = cos(90° - 12°) = sin 12°
sec 78° = sec(90° - 12°) = cosec 12°
⇒ sin 12° + cosec 12°

(v) cosec 54° + sin 72°

Solution

cosec 54° = cosec(90° - 36°) = sec 36°
sin 72° = sin(90° - 18°) = cos 18°
⇒ sec 36° + cos 18°

(vi) cot 85° + cos 75°

Solution 

cot 85° = cot(90° - 5°) = tan 5°
cos 75° = cos(90° - 15°) = sin 15°
= tan 5° + sin 15°

(vii) sin 67° + cos 75°

Solution

sin 67° = sin(90° - 23°) = cos 23°
cos 75° = cos(90° - 15°) = sin 15°
= cos 23° + sin 15°

4. Express cos 75° + cot 75° in terms of angles between 0° and 30°. 

Solution

cot 75° = cos(90° - 15°) = sin 15°
cot 75° = cot(90° - 15°) = tan 15°
= sin 15° + tan 15°

5. If sin3A = cos(A - 26°), where 3A is an acute angle, find the value of A = ? 

Solution

Cos θ = sin (90° - θ)
⇒ cos(A - 26) = sin(90° - (A - 26°) ]
⇒ sin 3A = sin(90° - (A - 26°)]
Equating angles on both sides 
3A = 90° - A + 26°
4A = 116° 
A = 116°/4 = 29°
∴ A = 29°

6. If A, B, C are interior angles of a triangle ABC, prove that

(i) tan[(c + a)/2 = cot(B/2)

(ii) sin (B+C)/2 = cos A/2

Solution 

7. Prove that 

(i) tan 20° tan 35° tan 45° tan 55° tan 70° = 1 

Solution

tan 20° = tan(90° - 70°) = cot 70°
tan 35° = tan(90° - 70°) = cot 55°
tan 45° = 1 
⇒ cot 70° tan 70° × cot 55° tan 55° × tan 45° cot θ = tan θ = 1 
⇒ 1 × 1 × 1 = 1

Hence proved.

(ii) sin 48° sec 42° + cosec 42° = 2 

Solution

sin 48° = sin(90° - 42°) = cos 42°
cos 45° = cos(90° - 42°) = sin 42°
sec θ . cos θ = 1 . sin θ cosec θ = 1 
⇒ cos 42° sec 42° + sin 42° cosec 42°
⇒ 1 + 1  = 2 
∴ LHS = RHS

(iii) sin 70°/cos 20° + cosec 20°/sec 70° - 2 cos 70° cosec 20° = 0

Solution

sin(70°) = sin(90° - 20°) = cos 20°
cosec 20° = cosec(90° - 70°) = sec 70°
cos 70° = cos(90° - 20°) = sin 20° 
⇒ cos 20°/cos 20° + sec 70°/sec 70° - 2 sin20° cosec 20°
1 + 1 - 2(1) = 0 
∴ LHS = RHS

Hence proved

(iv) cos 80°/sin 10° + cos 59° cosec 31° = 2 

Solution

cos 80° = cos(90° - 10°) = sin 10°
cos 59° = cos(90° - 31°) = sin 31°
⇒ sin 10°/sin 10° + sin 31° cosec 31° 
= 1 + 1 = 2  [∵ sin θ cosec θ = 1]
Hence proved

8. Prove the following . 

(i) sin θ sin(90 - θ) - cosθ cos(90 -θ) = 0 

Solution

sin(90 - θ) = cos θ
cos(90 - θ) - cos θ sin θ  = 0 
∴ LHS = RHS 
Hence proved

(ii) [cos(90° - θ) sec(90° - θ) tanθ]/[cosec(90° - θ) sin(90° - θ) cot(90° - θ) + tan(90° - θ)/cotθ = 2 

Solution

cos(90° - θ) = sinA  
cosec(90° - θ) = sec θ 
sec(90° - θ) = cosec θ 
sin(90° - θ) = cos θ
cot(90° - θ) = tan θ

(iii) [tan(90° - A)cotA]/cosec² A - cos² A = 0 

Solution

tan(90 - A) = cot A 

(iv) [cos(90° - A) sin(90° - A)]/tan(90° - A) - sin² A = 0

Solution

(v) sin(50° + θ) - cos(40° - θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1 

Solution

sin(50° + θ ) = cos(90° - (50° + θ) = cos(40° - θ) 

tan 1 = tan(90° - 89°) . cot 89°
tan 10° = tan(90° - 80°) = cot 80°
tan 20° = tan(90° - 70°) = cot 70°
⇒ cos(40° - θ) - cos(40° - θ) = cots 89° tan 89°. cot 80° cot 70° tan 70° 
cot. tanθ = 1 
= 1 . 1 . 1 = 1 
LHS = RHS 
Hence proved

9. Evaluate : 

(i) 2/3 (cos⁴ 30° - sin⁴ 45°) - 3(sin² 60° - sec² 45°) + 1/4 cot² 30°

Solution

(ii) 4(sin² 30° + cos⁴ 60°) - 2/ 3 [{√(3/2)}² ・{1/√2}² } + 1/4 (√3)² 

Solution

(iii) sin 50°/cos 40° + cosec 40°/sec 50° - 4cos 50° cosec 40°

Solution

(iv) tan 35° tan 40° tan 50° tan 55°

Solution

tan 35° = tan (90° - 55°) = cot 55°
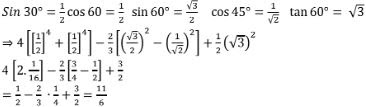
tan 40° = tan(90° - 50°) = cot 55°
tan 65° = 1 
cot 55° tan 55° cot 50° tan 50° tan 45° 
1 × 1× 1 = 1 

(v) cosec(65° + θ) - sec(25° -θ) - tan(55° - θ) + cot(35° + θ)

Solution

cosec(65° + θ) = sec(90° - (65° + θ)) = sec(25° - θ)
tan(55° - θ) = cot(90° - (55° - θ) = cot(35° + θ)
⇒ sec(25° - θ) - sec(25° -θ) tan (55° - θ) + tan(55° - θ) = 0  

(vi) tan 7° tan23° tan60° tan 67° tan83°

Solution 

tan 7° tan 23° tan 60° tan(90° - 23) tan(90° - 7°)
⇒ tan 7° tan 23° tan 60° cot 23° tan 60°
1×1× √3 = √3

(vii) 2sin 68°/cos 22° - 2 cot 15°/5 tan 75° - (8 tan 45° tan 20° tan40° tan 50° tan 70°)/5

Solution 

Sin 68° = sin(90° - 22°) = cos 22°
Cot 15° = tan(90° - 75°) = tan 75°

= 2 - 2/5 - 3/5 = 2 - 1 = 1

(viii) 3 cos 55°/ 7 sin 35° - 4(cos 70° cosec 20°)/7(tan 5° tan 25° tan 45° tan 65° tan 85°)

Solution 

(ix) sin 18°/cos 72° + √3[tan 10° tan 30° tan 40° tan 50° tan 80°]

Solution

(x) cos 58°/sin 32° + sin 22°/cos 68° - (cos 38° cosec 52°)/(tan 18° tan 35° tan 60° tan 72° tan 65°)

Solution 

10. If  sin θ = cos(θ - 45°), where θ - 45° are acute angles, find the degree measure of θ. 

Solution 

Sin θ = cos (θ - 45°)
Cos θ = cos (90 - θ)
Cos (θ - 45°) = sin(90° - (θ - 45°)) = sin(90° - θ + 45°)
Sin θ = sin (135 - θ)
θ = 135 - θ
2θ = 135 
∴ θ = 135/2

11. If A, B, C are the interior angles of a ΔABC, show that : 
(i) Sin (B+C)/2 = cos A/2  
(ii) cos (B+C)/2 = Sin A/2 

Solution 

A + B +C = 180 
B - C = 180 - A/2

12. If 2θ + 45° and 30° - θ are acute angles, find the degree measure of θ satisfying Sin(20 + 45°) = cos(30 - θ).

Solution 
Here 20 + 45° and  30 - θ° are acute angles: 

We know that (90 - θ) = cos θ
Sin (2θ + 45°) = sin (90 - (30 - θ))
Sin(2θ + 45°) = sin (90° - 30 + θ)

Sin(20 + 45°) = sin( 60 + θ)
On equating sin of angle of we get
2θ + 45 = 60 + θ 
2θ - θ = 60 - 45 
θ = 15°

13. If θ is a positive acute angle such that sec θ = cosec 60° , find 2 cos²θ – 1.

Solution 

We know that sec(90 - θ) = cosec²θ 
Sec θ = sec (90 - 60°)
On equating we get 
sec θ = sec 30°
θ = 30° 

14. If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.

Solution 

We know that sin(90 - θ) = cos θ
sin 2θ = cos 2θ
⇒ sin 4θ = sin(90 - 2θ)
⇒ 4θ = 90 - 2θ
⇒ 6θ = 90 
⇒ θ = 90/6
⇒ θ = 15°

15. If Sin 3θ = cos(θ - 6°) where 3 θ and θ - 6° are acute angles, find the value of θ. 

Solution 

3θ, θ - 6° are acute angle 
We know that sin(90 - θ) = cos θ
sin 3θ = sin(90 - (θ - 6°))
⇒ sin 3θ = sin(90 - θ + 6°)
⇒ sin 3θ = sin (96° - θ)
⇒ 3θ = 96° - θ 
⇒ 4θ = 96°

⇒ θ = 96°/4 
⇒ θ = 24°

16. If sec 4A = cosec(A - 20°) where 4A is acute angle, find the value of A. 

Solution 

sec 4A = sec [90 − A − 20] [∵ sec(90 − θ) = cosec θ]

⇒ sec 4A = sec (90 – A + 20)

⇒ sec 4A = sec (110 – A)

⇒ 4A = 110 – A

⇒ 5A = 110 
⇒ A = 110/5 = 22

17. If  sec 2A = cosec (A - 42°) where 2A  is acute angle. Find the value of A. 

Solution 

We know that [sec(90 – θ)) = cosec θ

sec 2A = sec (90 – (A – 42))

⇒ sec 2A = sec (90 – A + 42)

⇒ sec 2A = sec (132 – A)

Now equating both the angles we get

2A = 132 – A
⇒ 3A = 132/3 
⇒ A = 44