RD Sharma Solutions Chapter 3 Pair of Linear Equation in Two Variables Exercise 3.5 Class 10 Maths

RD Sharma Solutions for Class 10 Chapter 3 Pair of Linear Equation in Two Variables Exercise 3.5

Chapter Name

RD Sharma Chapter 3 Pair of Linear Equation in Two Variables

Book Name

RD Sharma Mathematics for Class 10

Other Exercises

  • Exercise 3.1
  • Exercise 3.2
  • Exercise 3.3
  • Exercise 3.4
  • Exercise 3.6

Related Study

NCERT Solutions for Class 10 Maths

Exercise 3.5 Solutions

In each of the following systems of equations determine whether the system has a unique solution , no solution or infinitely many solutions. In case there is a unique solution, find it : (1, -4)

1. x - 3y - 3 = 0 
3x - 9y - 2 = 0 

Solution

The given system of equations may be written as 
x - 3y - 3 = 0 
3x - 9y - 2 = 0 
The given system of equations is of the form 


2. 2x + y - 5 = 0 
4x + 2y - 10 = 0 

Solution

The given system of equation may be written as 
2x + y - 5 =0 
4x + 2y - 10 = 0 
The given system of equations is of the form 


3. 3x - 5y = 20 
6x - 10y = 40 

Solution

3x - 5y = 20 
6x - 10y = 40  
Compare it with 


4.  x - 2y - 8 = 0 
5x - 10y - 10 = 0 

Solution

The given system of equation may be written as 
x - 2y - 8 = 0 
5x - 10y - 10 = 0 
The given system if equation is of the form  


5. kx + 2y - 5= 0 
3x + y - 1 = 0 

Solution

The given system of equation is 
kx + 2y - 5= 0 
3x + y - 1 = 0
The system of equation is of the form 



6. 4x +5y + 8 = 0
2x + 2y+2 = 0
Solution


7.  4x - 5y = k
2x - 3y = 12
Solution

The given system of equation is 
4x - 5y - k = 0
2x - 3y - 12 = 0 
The system of equation is of the form 


8. x + 2y = 3
5x + ky + 7 = 0
Solution
The given system of equation is 
x + 2y - 3 = 0 
5x + ky + 7 = 0 
The system of equation is of the form 
Find the value of k for which each of the following systems of equations have definitely many solution : (9 - 19)

9. 2x + 3y - 5 = 0
6x - ky - 15 = 0
Solution

The given system of equation is 
2x + 3y - 5 = 0 
6x - ky - 15 = 0 
The system of equation is of the form 


10. 4x + 5y = 3
kx + 15y = 9

Solution

The given system of equation is 
4x + 5y - 3 = 0 
kx + 15y - 9 = 0 
The system of equation is of the form 



11. kx - 2y + 6 = 0
4x  + 3y + 9 = 0

Solution

The given system of equation is 
kx - 2y + 6 = 0
4x + 3y + 9 = 0 
The system of equation is of the form 


12. 8x + 5y = 9 
kx + 10y = 18 

Solution

The given system of equation is 
8x + 5y - 9  = 0 
kx + 10y - 18 = 0 
The system of equation is of the form 


13. 2x - 3y = 7
(k + 2)x - (2k + 1)y - 3(2k - 1)
Solution

The given system of equation may be written as 
2x - 3y - 7 = 0 
(k + 2)x - (2k + 1)y - 3(2k - 1) = 0 
The system of equation is of the form 


14. 2x + 3y = 2
(k + 2)x + (2k + 1)y - 2(k - 1)
Solution
The given system of equation may be written as 
2x + 3y - 2 = 0 
(k + 2)x + (2k + 1)y - 2(k - 1) = 0 
The system of equation is of the form 


15.  x + (k + 1)y = 4 
(k + 1)x + 9y - (5k + 2)
Solution

The given system of equation may be written as 
x + (k + 1)y - 4 = 0 
(k + 1)x + 9y - (5k + 2) = 0 
The system of equation is of the form 


16. kx + 3y - 2k + 1
2(k + 1)x + 9y - (7k + 1)
Solution

The given system of equation may be written as 
kx + 3y - (2k + 1) = 0  
2(k + 1)x + 9y - (7k + 1) = 0 
The system of equation is of the form 


Hence,  the given system of equations will have infinitely many solutions, if k = 2. 

17. 2x + (k - 2)y = k
6x + (2k - 1)y - (2k + 5)
Solution

The given system of equation may be written as 
2x + (k - 2)y - k = 0 
6x + (2k - 1)y - (2k + 5) = 0 
The system of equation is of the form 

 


18. 2x + 3y = 7 
(k + 1)x + (2k - 1)y - (4k + 1)

Solution

The given system of equation may be written as 
2x + 3y - 7  = 0 
(k + 1)x + (2k - 1)y - (4k + 1) = 0 
The system of equation is of the form 


19. 2x +3y = k 
(k - 1)x + (k + 2)y - 3k
Solution

The given system of equation may be written as 
2x + 3y - k = 0 
(k - 1)x + (k + 2)y - 3k = 0 
The system of equation is of the form 


Find the value of k for which the following system of equations has no solultion: (20 - 25)

20. kx - 5y = 2
6x + 2y = 7
Solution
Given,
kx - 5y = 2
6x + 2y = 7
condition for system of equations having no solution

21. x + 2y = 0 
2x + ky - 5 = 0 
Solution
The given system of equation may be written as 

x + 2y = 0 
2x + ky - 5 = 0 
The system of equation is of the form 


22. 3x - 4y + 7 = 0 
kx  + 3y - 5 = 0 
Solution
The given system of equation may be written as 

3x - 4y + 7 = 0 
kx  + 3y - 5 = 0 
The system of equation is of the form 


23.  2x - ky +3 = 0
3x + 2y - 1 = 0
Solution
The given system of equation may be written as 

2x - ky +3  = 0 
3x + 2y - 1 = 0 
The system of equation is of the form 


24. 2x + ky - 11 = 0
5x - 7y - 5 = 0

Solution
The given system of equation is
2x + ky - 11 = 0
5x - 7y - 5 = 0
The system of equation is of the form 

25. kx + 3y = 3 
12x + ky = 6  
Solution

kx + 3y = 3 
12x + ky = 6  


26. For what value of α, the following system of equations will be inconsistent?
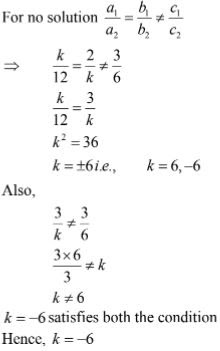
4x + 6y - 11 = 0
2x + ky - 7 = 0
Solution
The given system of equation may be written as 
4x + 6y - 11 = 0 
2x + ky - 7 = 0 

The system of equation is of the form 


27. For what value of α, the system of equation 
αx + 3y = α - 3 
12x + αy = α 
will have no solution ? 
Solution
The given system of equation may be written as 
αx + 3y - (α - 3) = 0 
12x + αy - α  = 0 
The system of equation is of the form 

28. Find the value of k for which the system 
kx + 2y = 5
3x + y = 1
has (i) a unique solution, and (ii) no solution.

Solution

The given system of equation may be written as 
kx + 2y - 5 = 0 
3x +y - 1 = 0 
It is of the form 


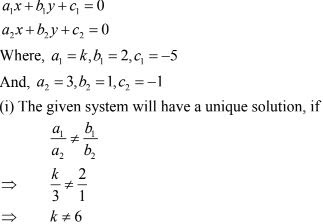
So, the given system of equations will have a unique solution , if k ≠ 6

(ii) The given system will have no solution, if 


29. Prove that there is a value of c (≠0) for which the system 
6x + 3y = c - 3 
12x + cy = c
has infinitely many solutions. Find this value. 

Solution

The given system of equation may be written as  
6x + 3y - (c - 3)= 0 
12x + cy - c = 0 
This is of the form 


30. Find the values of k for which the system 
2x + ky = 1 
3x - 5y = 7 
will have (i) a unique solution, and (ii) no solution . Is there a value of k for which the system has infinitely many solutions ?
Solution

The given system of  equation may be written as 
2x + ky - 1 = 0 
3x - 5y - 7 = 0 
It is of the form 


31. For what value of k, the following system of equations will represent the coincident lines ? 
x + 2y + 7 = 0
2x + ky + 14 = 0
Solution

The given system of equations may be written as 
x + 2y + 7 = 0 
2x + ky + 14 = 0 

The given system of equations is of the form 


32.  Obtain the condition for the following system  of linear equations to have a unique solution 
ax + by = c 
lx + my = n
Solution

The given system of equations may be written as 

ax + by - c = 0  
lx + my - n = 0 
It is of the form 


33. Determine the values of a and b so that the following system of linear equations have infinitely many solutions:
(2a - 1)x + 3y - 5 = 0
3x + (b-1)y - 2 = 0
Solution

The given system of equations may be written as 
(2a - 1)x + 3y - 5= 0 
3x +(b-1)y - 2 = 0 
It is of the form 


34. Find the values of a and b for which the following system of linear equations has infinite number of solutions : 
2x - 3y = 7
(a+b)x - (a+ b - 3)y = 4a + b
Solution

The given system of equations may be written as 
2x - 3y -7 = 0 
(a+b)x - (a+ b - 3)y - (4a + b) = 0 
It is of the form 


35. Find the values of p and q for which the following system of linear equation has infinite number of solutions:
2x - 3y = 9 
(p + q)x + (2p - q)y = 3(p + q + 1)

Solution

The given system of equations may be written as
2x - 3y - 9 = 0
(p + q)x + (2p - q)y - 3(p + q + 1) = 0 
It is of the form 


36. Find the values of a and b for which the following system of equations has infinitely many solutions : 
2x + 3y = 7 
(a-b)x + (a+ b)y = 3a + b - 2 
Solution
2x + 3y - 7 = 0
(a-b)x + (a+ b)y - (3a + b - 2 ) = 0 

(i) (2a - 1)x - 3y = 5 
3x + (b - 2)y = 3 
Solution

The given system of equations is 

(2a - 1)x - 3y - 5 = 0
3x + (b - 2)y - 3 = 0 
It is of the form 

(ii) 2x - (2a + 5)y = 5 
(2b + 1)x - 9y = 15 
Solution

The given system of equations is 

2x - (2a + 5)y - 5 = 0
(2b + 1)x - 9y - 15 = 0
It is of the form 

(iii) (a -)x + 3y = 2 
6x +(1 +2b)y = 6 
Solution

The given system of equations is 
(a -)x + 3y - 2 = 0 
6x +(1 +2b)y  - 6  = 0 
It is of the form 
Hence, the given system of equations will have infinitely many solutions, 
If a = 3 and b = -4. 

(iv) 3x + 4y = 12
(a +b)x + 2(a -b)y = (5a -1)
Solution

The given system of equations is 
3x + 4y - 12 
(a +b)x + 2(a -b)y - (5a -1) = 0 
It is of the form 


(v) 2x + 3y = 7
(a - 1)x + (a + 1)y = (3a - 1)
Solution

The given system of equations is 
2x + 3y - 7 = 0 
(a - 1)x + (a + 1)y - (3a - 1) = 0 
It is of the form 


(vi) 2x + 3y = 7
(a-1)x + (a+ 2)y = 3a
Solution

The given system of equations is 
2x + 3y - 7 = 0 
(a-1)x + (a+ 2)y - 3a  = 0 
It is of the form 

Tags
Previous Post Next Post