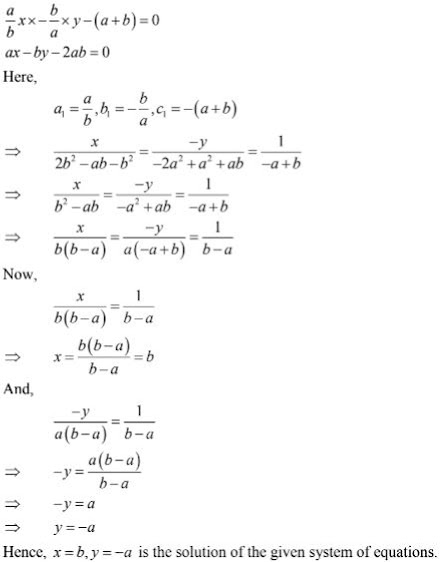RD Sharma Solutions for Class 10 Chapter 3 Pair of Linear Equation in Two Variables Exercise 3.4

RD Sharma Solutions Chapter 3 Pair of Linear Equation in Two Variables Exercise 3.4 Class 10 Maths

Chapter Name	RD Sharma Chapter 3 Pair of Linear Equation in Two Variables
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 3.1 Exercise 3.2 Exercise 3.3 Exercise 3.5 Exercise 3.6
Related Study	NCERT Solutions for Class 10 Maths

Exercise 3.4 Solutions

Solve each of the following systems of equations by the method of cross - multiplication: 

1. x + 2y + 1 = 0 
2x - 3y - 12 = 0 

Solution

2. 3x + 2y + 25 = 0 
2x + y + 10 = 0

Solution

The given system of equation is 
3x + 2y + 25 = 0 
2x + y + 10 = 0
Here, 

3. 2x + y - 35 = 0 
3x + 4y - 65 = 0 

Solution

4. 2x - y - 6 = 0 
x - y - 2 = 0

Solution

The given system of equations may be written as 
2x - y - 6 = 0 
x - y - 2 = 0
Here, 

5. (x+y)/xy = 2
(x-y)/xy = 6

Solution

6. ax + by = a-b
bx - ay = a + b

Solution

7. x + ay - b = 0 
ax - by -c = 0 

Solution

8. ax + by = a² .
bx + ay = b² 

Solution

9. x/a + y/b = 2 
ax - by = a² - b² 

Solution

10. x/a + y/b = a + b 

Solution

11. x/a = y/b
ax + by = a² + b² 

Solution

12. 5/(x+y) - 2/(x -y) = -1 
15/(x + y) + 7/(x - y) = 10, where x ≠ 0 and  y ≠ 0

Solution

13. 2/x + 3/y = 13 
5/x - 4/y = -2 , where x ≠ 0 and y ≠ 0 

Solution

14. ax + by = (a + b)/2
3x + 5y = 4 

Solution

15. 2ax + 3by = a + 2b
3ax + 2by = 2a + b

Solution

16. 5ax + 6by = 28
3ax + 4by = 18  

Solution

17. (a + 2b)x + (2a - b)y = 2 
(a - 2b)x + (2a + b)y = 3 

Solution

18. x(a- b + ab/a-b) = y(a+ b - ab/a+b)
x + y = 2a² 

Solution

19. ax[1/(a-b) - 1/(a+b)] + cy[1/(b-a) - 1/(b+a)] = 2a/(a+b)

Solution

20. (a - b)x + (a+ b)y = 2a²  -  2b² 
(a+b)(x+y) = 4ab

Solution

21. a²x + b²y = c²  
b²x + a²y = d²  

Solution

The given system of equations may be written as 
a²x + b²y - c²  = 0
b²x + a²y - d²  = 0 
Here, 

22. 57/(x+y) + 6/(x-y) = 5 
38/(x+y) + 21/(x-y) = 9 

Solution

23. 2(ax - by) + a + 4b = 0 
2(bx + ay) + b - 4a = 0 

Solution

The given system of equation may be written as 
2ax - 2by + a +4b = 0 
2bx + 2ay + b - 4a = 0 
Here, 

24. 6(ax + by) = 3a + 2b
6(bx - ay) = 3b - 2a

Solution

The given system of equation is 
6(ax + by) = 3a + 2b ...(i)
6(bx - ay) = 3b - 2a ...(ii)
From equation (i), we get 
6ax + 6by - (3a + 2b) = 0 ...(iii)
From equation (ii), we get 
6bx - 6ay - (3b - 2a) = 0 ...(iv)
Here, 

Hence, x = 1/2, y = 1/3  is the solution of the given system of equations. 

25. a²/x - b²/y = 0 
a²b/x + b²a/y = a + b, x, y ≠ 0 

Solution

Taking 1/x = u and 1/y = v. Then, the given system of equations become 

26. mx - my = m²  + n²  
x + y = 2m 

Solution

The given system of equations may be written as 
mx - ny - (m²  + n²) = 0 
x + y - 2m = 0 
Here, 

27. ax/b - by/a = a+ b
ax - by = 2ab 

Solution

The given system of equation may be written as 

28.(b/a)x + (a/b)y - (a²  + b²) = 0 
x + y - 2ab = 0 

Solution