ICSE Revision Notes for Similarity Class 10 Maths
Chapter Name | Similarity |
Topics Covered |
|
Related Study |
Difference Between Similarity and Congruence
Congruency of line segments:
“Two line segments are congruent to each other if their lengths are equal”.
Consider the following line segments.
Here, the line segments AB and PQ will be congruent to each other, if they are of equal length.
Conversely, we can say that, “Two line segments are of equal length if they are congruent to each other”.
Congruency of angles:
“Two angles are said to be congruent to each other if they have the same measure”.
The angles shown in the following figures are congruent to each other as both the angles are of the same measure 45°.
Thus, we can write ∠BAC ≅ ∠QPR.
Its converse is also true.
“If two angles are congruent to each other, then their measures are also equal”.
There is one special thing about congruent figures that their corresponding parts are always equal.
For example, if two triangles are congruent then their corresponding sides will be equal. Also, their corresponding angles will be equal.
Look at the following triangles.
Here, ΔABC ≅ ΔDEF under the correspondence ΔABC ↔ ΔDEF. This correspondence rule represents that in given triangles, AB ↔ DE (AB corresponds to DE), BC ↔ EF, CA ↔ FD, ∠A ↔ ∠D, ∠B ↔ ∠E, ∠C ↔ ∠F.
These are corresponding parts of congruent triangles (CPCT), ΔABC and ΔDEF.
Since ΔABC and ΔDEF are congruent, their corresponding parts are equal.
Therefore, AB = DE, BC = EF, CA = FD
And, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
Similarly, we can apply the method of CPCT on other congruent triangles also.
Let us now try and apply what we have just learnt in some examples.
Example 1: Find which of the pairs of line segments are congruent.
(i)
(i) Lengths of the two line segments are not same. Therefore, they are not congruent.
(ii) Each of the line segments is of length 3.1 cm, i.e. they are equal. Therefore, they are congruent.
Example 3: If ∠ABC ≅∠PQR and ∠PQR = 75o, then find the measure of ∠ABC.
Answer
If two angles are congruent, then their measures are equal.
Since ∠ABC ≅ ∠PQR,
∴ ∠ABC = ∠PQR
Therefore, ∠ABC = 75o
Example 4: Which of the following pairs of angles are congruent?
(i)
(ii)
Answer
(i) The measure of both the angles is the same. Therefore, they are congruent.
(ii) The measures of the two angles are different. Therefore, they are not congruent.
Example 5: Identify the pairs of similar and congruent figures from the following.
(i)
(ii)
(iii)
(iv)
(v)
(vi)(vii)
(viii)
AnswerFigures (i) and (iii) are similar because their corresponding angles are equal and their corresponding sides are in the same ratio. However, these figures are not congruent as they are of different sizes.
Figures (ii) and (viii) are congruent as they are of the same shape and size (circles with radius 1 cm each).
Example 6: Are the following figures similar or congruent?
The two given figures show two one-rupee coins. As both the figures represent the same coin in two different sizes, they are similar to each other. However, the pictures are not congruent because of their different sizes.
Example 7: In the following figure, ΔPQR and ΔSTU are congruent.
If PQ = 8 cm, QR = 6 cm then find the perimeter of ΔSTU.
Answer
In ΔPQR, we have
PQ = 8 cm, QR = 6 cm and ∠Q = 90°
Applying Pythagoras theorem in ΔPQR, we obtain
RP2 = PQ2 + QR2
⇒ RP2 = 82 + 62
⇒ RP2 = 64 + 36
⇒ RP2 = 100
⇒ RP = 10 cm
Since ΔPQR and ΔSTU are congruent, their corresponding parts will be equal. Therefore,
PQ = 8 cm = ST (CPCT)
QR = 6 cm = TU and (CPCT)
RP = 10 cm = US (CPCT)
∴ Perimeter of ΔSTU = ST + TU + US = 8 cm + 6 cm + 10 cm = 24 cm
AAA Criterion of Similarity of Triangles
We can check the similarity of any two triangles using AAA criterion of similarity if any two angles of each triangle are given so, AAA criterion is same as AA criterion.
AA criterion "If two triangles are equiangular, then their corresponding sides are proportional." can be proved as below.
Given: ΔABC and ΔPQR where ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R.
To prove: AB/PQ = BC/QR = CA/RP
Construction: Mark X and Y on AB and AC respectively such that AX = PQ and AY = PR.
Proof:
In ΔAXY and ΔPQR,
AX = PQ [By construction]
∠A = ∠P [Given]
AY = PR [By construction]
So, by SAS postulate, ΔAXY ≡ ΔPQR.
[Note: The symbol '≡' stands for congruency]
⇒XY = QR and ∠X = ∠Q [CPCT]
Now, ∠X = ∠B [∠X = ∠Q = ∠B]
∴ XY || BC [∠X and ∠B are corresponding angles]
∴ AB/AX = AC/AY = BC/XY
⇒ AB/PQ = CA/PR = BC/QR
Hence, AA criterion is proved.
Now, look at the following triangles.
Here, ∠B = ∠E = 50°
and ∠C = ∠ F = 40°
Then, using AAA similarity criterion, ΔABC is similar to ΔDEF.
In symbolic form, we can write ΔABC ∼ ΔDEF. In symbolic form, the order of vertices is very important. For the above triangles, we cannot write ΔABC ∼ ΔEFD because ∠B = ∠E and ∠C = ∠F
Converse of AAA criterion is also true which states that:
If two triangles are similar then their corresponding angles are equal.
For example, if ΔABC ∼ ΔDEF then ∠A = ∠D, ∠B = ∠E and ∠C = ∠ F.
Note: In some state boards, the symbol "|||"is used for similarity.
I.e., ΔABC ∼ ΔDEF may also be written as ΔABC ||| ΔDEF.
Let us now look at some more problems based on AAA similarity criterion.
Example 1: In the following figure, if DE || BC, then prove the following.
(a) ΔABC ∼ ΔADE
(b) ΔDFE ∼ ΔCFB
Answer
(a) In ΔABC and ΔADE,
∠BAC = ∠DAE (Common to both)
∠ADE = ∠ABC (Since DE is parallel to BC, ∠ADE and ∠ABC are corresponding angles)
By AAA similarity criterion,
ΔABC ∼ ΔADE
(b) In ΔDFE and ΔBFC,
∠DFE = ∠BFC (Vertically opposite angles)
∠EDF = ∠BCF (Alternate angles)
By AAA similarity criterion,
ΔDFE ∼ ΔCFB
Example 2: In the given figure, if WY || ZX, then prove that ΔOWY ∼ ΔOXZ.
Answer
Here, WY || ZX
Now, in ΔOWY and ΔOZX,
∠WOY = ∠ZOX (Vertically opposite angles)
∠OWY = ∠OXZ (Alternate angles)
∠OYW = ∠OZX (Alternate angles)
By AAA similarity criterion of triangles,
ΔOWY ∼ ΔOXZ
SSS Criterion of Similarity of Triangles
Converse of SSS criterion is also true which states that:
If two triangles are similar then their corresponding sides are proportional.
For example, if ΔABC ∼ ΔPQR then AB/PQ = BC/QR = CA/RP.
Let us solve some problems to understand this concept better.
Example 1: If PQR is an isosceles triangle with PQ = PR and A is the mid-point of side QR, then prove that ΔPAQ is similar to ΔPAR.
Answer
It is given that ΔPQR is an isosceles triangle and PQ = PR.
Also, A is the mid-point of QR, therefore
QA = AR
And, PA = PA (Common to both triangles)
Therefore, we can say that
PQ = PR = QA/AR = PA/PA
∴ Using SSS similarity criterion, we obtain
ΔPAQ ∼ ΔPAR
Example 2: In the following figure, E and D are the mid-points of the sides BC and AC respectively. Prove that ΔABC ∼ ΔDEC.
AnswerIt is given that E is the mid-point of BC.
∴ BE = EC
Now, BC = BE + EC
⇒ BC = 2EC
⇒ BC/EC = 2/1
Similarly, D is the mid-point of AC, therefore
AC = 2DC
⇒ AC/DC = 2/1
Also, from the figure,
By SSS criterion of similarity of triangles,
ΔABC ∼ ΔDEC
Example 3: In the following figure, the lines XC and YC of same length are drawn such that C is the mid-point of AB. If AX = BY, then find the measure of the following angles.
∠BYC (c) ∠CAX
∠CBY (d) ∠ACX
AnswerIn the triangles CAX and CBY,
CX = CY (Given)
CA = CB (C is the mid-point of AB)
AX = BY (Given)
Therefore, by SSS similarity criterion,
ΔCAX ∼ ΔCBY
We know that the corresponding angles of similar triangles are equal. ∴ ∠AXC = ∠BYC = 40°
⇒ ∠BYC = 40°
Also, ∠ACX = ∠BCY
Let ∠ACX = ∠BCY = x
Therefore, x + x + 120° = 180° (∠ACX, ∠BCY, and ∠XCY form a linear pair)
⇒ 2x = 180° − 120° = 60°
⇒ x = 30°
∴ ∠ACX = ∠BCY = 30°
Now, by angle sum property in ΔACX, we obtain
30° + ∠CAX + 40° = 180°
⇒ ∠CAX = 180° − 70° = 110°
∴ ∠CBY = ∠CAX = 110°
Thus, we obtain
- ∠BYC = 40°
- ∠CBY = 110°
- ∠CAX = 110°
- ∠ACX = 30°
Example 4: ABCD is a square and PQS is an isosceles triangle with PQ = PS and R is the mid point of QS. If ΔABD ∼ ΔRPQ, then prove that ΔCBD ∼ ΔRPS.
Answer
ABCD is a square and PQS is an isosceles triangle.
Therefore, AB = BC = CD = DA
And, PQ = PS
In ΔABD and ΔCBD,
AB = CB (Sides of a square)
BD = BD (Common side)
DA = DC (Sides of a square)
By SSS similarity criterion,
ΔABD ∼ ΔCBD … (2)
Now, in ΔRPQ and ΔRPS,
RP = RP (Common side)
PQ = PS (Equal sides of an isosceles triangle)
QR = SR (R is the mid-point of QS)
Therefore, ΔRPQ ∼ ΔRPS … (3)
However, ΔABD ∼ ΔRPQ
Therefore, from (2) and (3), we obtain
ΔCBD ∼ ΔRPS
SAS Criterion of Similarity of Triangles
Look at the following figures.
Is there any similarity between them?
We can see that in both the triangles, the lengths of two sides are given and also the measure of the included angle is given. Now, let us compare the sides of the triangles and observe the result we obtain.
On taking the ratio of the sides, we obtain
AB/DE = AC/DF = 3/2
Therefore, we observe that the sides of the triangles are in the same ratio i.e., we can say that the sides of the triangles are proportional.
Using the above fact, can we say that the given triangles are similar?
To know the answer, let us first know about a similarity criterion known as SAS similarity criterion.
SAS similarity criterion can be stated as follows.
“If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar”.Using this criterion, we can check the similarity of any two triangles, if the two sides and the included angle between them are given.
In the above example, ∠A = ∠D = 65° and the sides including these angles are in the same proportion i.e., 3/2. Thus, we can say that ΔABC is similar to ΔDEF.
In symbolic form, we can write ΔABC ∼ ΔDEF. For writing the symbolic form, the order of the vertices is very important.
For example, consider the following figure.
Therefore, we can write ΔABC ∼ ΔEFD.
Let us now look at some more examples to understand this concept better.
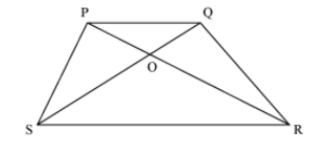
Example 1: If PQRS is a parallelogram, then prove that ΔSOR is similar to ΔPOQ.
AnswerConsider ΔSOR and ΔPOQ.
Since PQRS is a parallelogram, the diagonals bisect each other.
∴ SO = OQ and PO = OR
and ∠POQ = ∠SOR (Vertically opposite angles)
By SAS similarity criterion, we obtain
ΔSOR ∼ ΔQOP
Example 2: ΔABC is an isosceles triangle with AB and AC as the equal sides. The points D and E divide the side BC into three equal parts as shown in the figure. Prove that ΔABD ∼ ΔACE.
AnswerSince ABC is an isosceles triangle,
AB = AC
∠ABC = ∠ACB (Angles opposite to equal sides are equal in an isosceles triangle) It is given that the points D and E divide the side BC in three equal parts. Therefore, BD = DE = EC
In ΔABD and ΔAEC,
AB = AC
BD = EC
∠ABD = ∠ACE
By SAS similarity criterion,
ΔABD ∼ ΔACE
Basic Proportionality Theorem and its Converse
Consider the following figure.
In the above figure, DE is parallel to AF and DF is parallel to AC. Can we say that point E divides BF in the same ratio in which point F divides BC?
For this, we have to prove that (BE/EF = BF/FC).
To prove it, we should have the knowledge of basic proportionality theorem (Thales theorem).
Now, let us solve the problem discussed in the beginning with the help of BPT. In ABF, we know that AF is parallel to DE.
Thus, using BPT,
BD/DA = BE/BF … (1)
Similarly, in ABC, DF is parallel to AC.
Thus, using BPT,
BF/FC = BD/DA …(2)
From equations (1) and (2), we obtain
BE/EF = BF/FC
Thus, we can say that point E divides BF in the same ratio in which point F divides BC.
The converse of BPT is also true, which can be stated as follows.
“If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side”.
Corollary of BPT
If a line is drawn parallel to a side of a triangle, then the sides of the new triangle formed are proportional to the sides of the given triangle.
i.e, In the given figure, if DE || AB, then CD/CA = DE/AB = CE/AB
Applications of Basic Proportionality Theorem:
There are two very important properties based on BPT which are as follows:
- Property of intercepts made by three parallel lines on a transversal.
- Property of angle bisector of a triangle.
Let us discuss these properties in detail along with their proofs.
Property 1: Intercept Theorem
The lengths of the intercepts made by three parallel lines on one transversal are in the same ratio as the lengths of the corresponding intercepts made by the same lines on any other transversal.
Let us prove this property.
Given: line l || line m || line n
Transversal x intersects these lines at points P, Q and R while transversal y intersects these lines at points S, T and U.
To prove: PQ/QR = ST/TU
Construction: Draw a line segment PU intersecting line m at point M.
Proof:
In ΔPRU, we have
QM || RU
∴ PQ/QR = PM/MU ...(1) ...(By BPT)
Similarly, in ΔUSP, we have
TM || SP
∴ UM/MP = UT/TS ...(By BPT)
⇒ PM/MU = ST/TU
⇒ PQ/QR = ST/TU .... [Using (1)]
Hence proved.
Property 2: Angle Bisector Theorem
In a triangle, the angle bisector divides the side opposite to the angle in the ratio same as the ratio of remaining sides.
Let us prove this property.
Given: In ΔPQR, ray RT bisects ∠PRQ.
To prove: PT/TQ = PR/RQ
Construction: Draw a ray from Q parallel to ray RT such that it intersects extended PR at S.
We have,
RT || QS and PS is transversal
∴ ∠PRT = ∠RSQ ...(1) (Corresponding angles)
Considering other transversal RQ, we obtain
∠TRQ = ∠RQS ...(2) (Alternate angles)
But ∠PRT = ∠TRQ (RT bisects ∠PRQ)
∴ ∠RSQ = ∠RQS [Using (1) and (2)]
Thus, in ΔRQS,
RS = RQ ...(3) (Side opposite to equal angles are equal)
Now, in ΔPQS, we have
RT || QS
Hence proved.
Property 3: Converse of Angle Bisector Theorem
If a straight line through one vertex of a triangle divides the opposite side in the ratio of the other two sides, then the line bisects the angle at the vertex.
Let us prove this property.
QT/TR = PQ/PR
To prove: PT bisects ∠QPR i.e., ∠QPT = ∠RPT
Construction: Draw a ray from R parallel to ray PT such that it intersects extended QP at S.
Proof:
Since PT ∥ SR, then
QT/TR = QP/PS ...(1) (Basic Proportionality Theorem)
And we have,
QT/TR = QP/PR ...(2) (Given)
From (1) and (2) we have,
QP/PR = QP/PS
⇒ PS = PR
Now in ∆PSR, ∠PSR = ∠PRS ...(3)
If PT ∥ SR, then
∠TPR = ∠PRS ...(4) (Alternate Interior Angles)
∠QPT = ∠PSR ...(5) (Corresponding Angles)
From (3), (4) and (5) we get
∠QPT = ∠TPR
∴ PT bisects ∠QPR
Hence proved
These properties are very useful sometimes.
Let us now solve some examples based on BPT, its converse and properties related to BPT.
Example 1: In triangle ABC, D and E are points on the sides AB and AC, such that AB = 11.2 cm, AD = 2.8 cm, AC = 14.4 cm, and AE = 3.6 cm. Show that DE is parallel to BC.
AnswerIt is given that,
AB = 11.2 cm, AD = 2.8 cm, AC =14.4 cm, and AE = 3.6 cm
Therefore, BD = AB – AD = 11.2 – 2.8 = 8.4 cm
And,
EC = AC – AE = 14.4 – 3.6 = 10.8 cm
Now,
AD/DB = 2.8/8.4 = 1/3 and AE/EC = 3.6/(10.8) = 1/3
⇒ AD/DB = AE/EC
Thus, DE divides sides AB and AC of triangle ABC in the same ratio. Therefore, by the converse of BPT, we obtain that DE is parallel to BC.
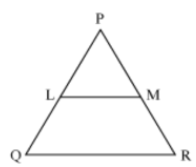
Example 2: In the figure shown below, find the length of PM, if it is given that LM || QR. The corresponding measures are shown in the figure.
AnswerHere, LM || QR
Then, using basic proportionality theorem, we obtain
Let PM = x cm
Then, MR = 12 – x cm
And, PL = 2 cm
LQ = 10 cm – 2 cm = 8 cm
On putting these values in equation (i), we obtain
2/8 = x/(12 – x)
⇒ 2(12 – x) = 8x
⇒ 24 – 2x = 8x
⇒ 24 = 8x + 2x
⇒ 24 = 10x
⇒ x = 2.4 cm
Thus, PM = 2.4 cm
Example 3: If ABCD is a trapezium with AD || BC, then prove that AO/CO = DO/BO, where O is the point of intersection of diagonals AC and BD.
Answer
A trapezium has been shown in the following figure.
A line LM is drawn parallel to AD and BC and passing through O.
Here, LO || BC.
Using BPT in ΔABC,
AL/LB = AO/CO ...(i)
Similarly, using BPT in ΔABD as LO || AD, we obtain
AL/LB = DO/BO ...(ii)
From equations (i) and (ii), we obtain
AO/CO = DO/BO
Hence, proved
Example 4: In ΔPQR, LM || QR and L is the mid-point of side PQ. Show that PM = MR.
AnswerHere, LM || QR
Using basic proportionality theorem (BPT),
PL/LQ = PM/MR ...(i)
Now, L is the mid-point of PQ.
∴ PL = LQ
Using this in equation (i), we obtain
LQ/LQ = PM/MR
PM/MR = 1
∴ PM = MR
Hence, proved
Example 5: In trapezium ABCD, AB || EF || DC. Find the length of BF and FC.
AnswerIn trapezium ABCD, AB || EF || DC.
Here, AD and BC are transversals to parallel segments AB, EF and DC.
Intercepts made by AD are AE and ED while intercepts made by BC are BF and FC.
Using property of intercepts made by three parallel lines on a transversal, we obtain
AE/ED = BF/FC
⇒ 9/6 = BF/FC
⇒ FC = 6/9.BF ...(1)
Now,
BF + FC = 10
⇒ BF + 6/9BF = 10
⇒ 15/9 BF = 10
⇒ BF = 6
∴ FC = 6/9 × 6 = 4
Thus, BF = 6 cm and FC = 4 cm.
Example 6: In ΔABC, BD bisects ∠ABC. Find the length of AD.
AnswerIn ΔABC, BD bisects ∠ABC
Thus, by using the property of angle bisector of a triangle, we obtain
AB/BC = AD/CD
⇒ 6/8 = AD/2
⇒ AD = 1.5
Hence, the length of AD is 1.5 cm.
Example 7: In the given figure, DE || AB. If perimeter of ΔABC: perimeter of ΔCDE = 4:5 and DE = 1.2 cm, then find the length of AB.
It is given that, perimeter of ΔABC : perimeter of ΔCDE = 4:5 and DE = 1.2.
In ΔABC, DE || AB.
By applying the corollary of basic proportionality theorem, we get
CD/DA = CE/CB = DE/AB = k (= say)
CD = kCA, CE = kCB, DE = kAB
CD + CE + DE = k(CA + CB + AB)
Perimeter of ΔCDE/kPerimeter of ΔABC
Perimeter of ΔCDE/kPerimeter of ΔABC = k
∴ CD/DA = CE/CB = DE/AB = (Perimeter of ΔCDE)/(Perimeter of ΔABC)
⇒ 1.2/AB = 5/4
⇒ AB = 1.2 × 5/4 = 1.5 cm
Areas of Similar Triangles
We know what similar triangles are. Now, let us learn about an interesting theorem related to areas of similar triangles.
The theorem states that:
The ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Let us prove this theorem.
Given: ΔABC ∼ ΔXYZ
To prove: A(ΔABC)/A(ΔXYZ) = AB2/XY2 = BC2/YZ2 = CA2/ZX2
Construction: Draw segment AD perpendicular to BC and segment XP perpendicular to YZ.
Proof:
From the figure, we haveA(ΔABC) = 1/2 × BC × AD
And, A(∆XYZ) = 1/2 × YZ × XP
∴ A(∆ABC)/A(∆XYZ) = (BC × AD)/(YZ × XP) ....(1)
Since ∆ABC ~ ∆XYZ, we have
∠B = ∠Y, AB/XY = BC/YZ = CA/ZX ....(2)
In ∆ADB and ∆XPY, we have
∠B = ∠Y
∠ADB = ∠XPY (Both are right angles)
∴ ∆ADB ~ ∆XPY (Using AA similarity test)
∴ AB/XY = AD/XP ...(3)
∴ A(∆ABC)/A(∆XYZ) = BC/YZ × AB/XY [Using (1) and (3)]
⇒A (∆ABC)/A(∆XYZ) = AB/XY × AB/XY [Using (2)]
⇒ A(∆ABC)/A(∆XYZ) = AB2/XY2
Similarly, it can be shown that
A(∆ABC)/A(∆XYZ) = BC2/YZ2 and A(∆ABC)A(∆XYZ) = CA2/ZX2
∴ A(∆ABC)/A(∆XYZ) = AB2/XY2 = BC2/YZ2 = CA2/ZX2
Thus, the ratio of areas of similar triangles is equal to the ratio of squares of their corresponding sides.
Let A1 and A2 be the areas of similar triangles and s1 and s2 be their corresponding sides.
Then,
A1/A2 = (s1)2/(s2)2 = (s1/s2)2
Now, let us learn to apply this formula with the help of an example.
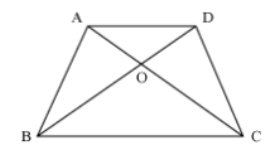
Consider a trapezium PQRS in which SR = 3 PQ. The diagonals PR and QS intersect each other at O.
If the area of ΔPOQ is 9 square cm, then what will be the area of ΔSOR?
Relation between areas, heights, medians and perimeters of similar triangles:
Let A1 and A2 be the areas of two similar triangles such that s1 and s2 are their corresponding sides, h1 and h2 are their corresponding heights, m1 and m2 are their corresponding medians and P1 and P2 are their respective perimeters.
Then,
A1/A2 = (s1)2/(s2)2 = (h1)2/(h2)2 = (m1)2/(m2)2 = (P1)2/(P2)2
Let us go through some examples based on the areas of similar triangles.
Example 1: The ratio of areas of two similar triangles is 16:25. Find the ratio of their corresponding sides.
Answer
We know that,
Ratio of areas of similar triangles = (Ratio of corresponding sides)2
⇒ 16/25 = (Ratio of corresponding sides)2
Ratio of corresponding sides =
= 4:5
Example 2: The areas of two similar triangles are 25 cm2 and 100 cm2. If one side of the first triangle is 4 cm, then find the corresponding side of the other triangle.
Answer
Let ABC and DEF be two triangles whose areas are 25 cm2 and 100 cm2respectively.
Let AB = 4 cm
Then, we have to find DE.
Since the two triangles ABC and DEF are similar,
∴ Area of ∆ABC/Area of ∆DEF = (AB)2/(DE)2
25/100 = (4)2/(DE)2
⇒ 1/4 = 16/(DE)2
⇒ (DE)2 = 16 × 4
⇒ (DE)2 = 64
⇒ DE = 8 cm
Thus, the corresponding side of the other triangle is 8 cm.
Example 3: In a triangle ABC, X, Y, and Z are the mid-points of the sides BC, AC, and AB respectively. Find the ratios of the areas of ΔABC and ΔXYZ.
Answer
Here, X, Y, and Z are the mid-points of sides BC, AC, and AB respectively.We know that the line joining the mid-points of two sides is parallel to the third side and its length is half of the third side.
∴ XY || AB and XY = AB/2
YZ || BC and YZ = BC/2
Again, XZ || AC and XZ = AC/2
As, XY || AB, YZ || BC, and XZ || AC,
∴ Quadrilaterals AYXZ, BXYZ, and CXZY are parallelograms.
∴ ∠BAC = ∠ZXY, ∠ABC = ∠ZYX, and ∠ACB = ∠XZY
Using AAA similarity criterion, we obtain
ΔABC ∼ ΔXYZ
∴ Area of ΔABC/(Area of ΔXYZ) = (AB/XY)2
Area of ΔABC/Area of ΔXYZ = ((AB)/(AB/2)2
Area of ΔABC/(Area of ΔXYZ) = 4/1
Area of ΔABC : Area of ΔXYZ = 4:1
Example 4: In the given figure, AB and CD are perpendiculars to the line segment BC. Also, AB = 5 cm, CD = 8 cm, and area of ΔAOB is 175 cm2. Find the area of ΔCOD.
AnswerHere, ΔAOB and ΔDOC are similar triangles because
∠ABO = ∠DCO (Each 90°)
∠AOB = ∠COD (Vertically opposite angles)
Therefore, by AAA similarity criterion,
ΔAOB ∼ ΔDOC
∴ (Area of ΔAOB)/(Area of ΔDOC) = (AB/CD)2
175/(Area of ΔDOC) = (5)2/(8)2
Area of ΔDOC = (175 × 64)/25
= 7 × 64
= 448 cm2
Thus, the area of ΔCOD is 448 cm2.
Maps and Models
The concept of similarity has a lot of applications in real life.
Let us see how this concept is used in maps and models.
In maps, the distance between any two objects is proportional to the actual distance between the two objects. Thus, the map and the object are similar to each other.
Maps are always drawn by taking a suitable scale.
For example, the distance between Anshika’s and Nakul’s houses is 500 m.
If we draw the map of their locality, then we cannot mark their houses 500 m apart. This is because this distance is very large. So, we need to choose a suitable scale.
Let us choose the scale as 100 m = 1 cm
Then, the distance between their houses on the map = 5 cm
The scale of a map can also be written in the form of a ratio.
“The scale of a map can be defined as the ratio of the distance between two points on the map to the actual distance of these two points on the ground.”
The scale given in the above example can be written as 1 : 100.
This ratio is known as the scale factor, and is denoted by the letter k.
∴ k = 1/100
The lengths in the model of an object are proportional to the actual lengths of the object. In the case of models:
k = (Length of the model)/(Length of the object) = (Height of the model)/(Height of the object)
Let us learn some facts about the scale factor.
(1) If the scale factor is k, then each side of the model is k times the corresponding side of the object.
(2)
|
Scale factor |
Transformation |
Size |
|
k = 1 |
Identify transformation |
Size of model = Size of the object |
|
k > 1 |
Enlargement |
Size of the model > Size of the object |
|
k < 1 |
Reduction |
Size of the model < Size of the object |
Let us solve some examples based on maps and models.
Example 1: An architect makes the model of a resort. There is a swimming pool in the resort. The dimensions of the swimming pool in the model are 8 cm × 5 cm × 2 cm.
What is the capacity of the pool in the resort? The scale factor is 1/100.
Answer
In the case of the model:
Length of the pool = 8 cm
Breadth of the pool = 5 cm
Depth of the pool = 2 cm
Length of the actual pool = 1/k × Length of the model
= 1/(1/100) × 8
= 800 cm = 8 m
Breadth of the actual pool = 1/k × Breadth of the model
1/(1/100) × 5 cm = 500 cm = 5 m
Depth of the actual pool = 1/k × Depth of the model
= 1/(1/100) × 2 cm = 200 cm = 2 m
Volume of the actual pool = 8 m × 5 m × 2 m
= 80 sq. m
Thus, the capacity of the pool in the resort is 80 sq. m.