ICSE Revision Notes for Loci Class 10 Maths
Chapter Name | Loci |
Topics Covered |
|
Related Study |
Locus
Let us look at the following figure.
This is a circle with centre at O; and P, Q and R are points on it.
Now, the question arises − what is a circle?
A circle is a set of points, which are equidistant from a fixed point. The fixed point is called the centre and the fixed distance is called the radius of the circle.
Does the circle satisfy any geometrical condition?
Yes, it does. The geometrical condition is that “the set of all points are equidistant from a fixed point”. Such geometrical condition satisfied by a circle for all points on it is called locus.
Therefore, locus can be defined as:
The locus is the set of all those points, which satisfy the given geometrical condition(s).
Or
The locus of a point is the path traced out by the point moving under given geometrical condition(s).
Clearly, circle is a locus of a point equidistant from a fixed point.
Similarly, we can define a parallel line to a fixed line as “the locus of point equidistant from a fixed line” as shown below:
There are two theorems associated with locus. These are explained below.
Theorem 1: The locus of a point, which is equidistant from two fixed points, is the perpendicular bisector of the line segment joining the two fixed points.
The converse of the above theorem can be stated as:
Any point on the perpendicular bisector of a line segment joining two fixed points is equidistant from the fixed points.
Theorem 2: The locus of a point, which is equidistant from two intersecting straight lines, consists of a pair of straight lines, which bisect the angle between the two given lines.
The converse of the above theorem can be stated as:
Any point on the bisector of an angle is equidistant from the arms of the angle.
Let us understand locus in some standard cases.
(1) The locus of a point, which is inside a circle and is equidistant from two different fixed points on the circle, is the diameter of the circle and it is perpendicular to the chord joining the points.
(2) If A and B are fixed points, then the locus of a point P such that ∠APB = 90° is the circle with AB as diameter.
Let us solve some examples in order to understand these concepts better.
Example 1: The internal bisectors of angles A, B, and C intersect each other at I. Let M be a point on BC and IM ⊥ BC. A point P moves so that it maintains a distance of IM from I. What is the locus of P? Justify your answer.
Answer
The locus of point P will be the incircle of ΔABC as shown below.
Let IL ⊥ AC and IN ⊥ AB
Now, in ΔBIN and ΔBIM,
BI = BI (Common)
∠IBN = ∠IBM (Angle bisector)
∠BNI = ∠BMI (Each 90°)
∴ ΔBIN ≅ ΔBIM (AAS congruence)
Therefore, by CPCT,
IN = IM
Similarly, it can be proved that IN = IL
∴ IM = IN = IL
That means the circle with centre I touches each side of ΔABC. Therefore, the locus of point P is an incircle of ΔABC.
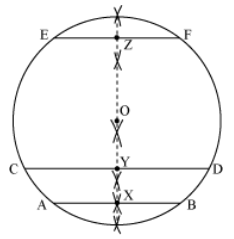
Example 2: Draw a circle of radius 4 cm. Draw three parallel chords of this circle. Join the mid-points of these chords. What can you say about the locus of the mid-points of these chords by looking at the figure?
Answer
Steps of construction:
(1) Draw a circle of radius 4 cm taking O as centre.
(2) Draw three parallel chords AB, CD, and EF parallel to each other. (3) Draw the perpendicular bisectors of these chords.
(4) Let the perpendicular bisectors intersect AB, CD, and EF at the points X, Y, and Z respectively.
(5) Join X to Y and Y to Z.