ICSE Revision Notes for Co-ordinate Geometry Class 10 Maths
Chapter Name | Co-ordinate Geometry |
Topics Covered |
|
Related Study |
Reflection of Figures
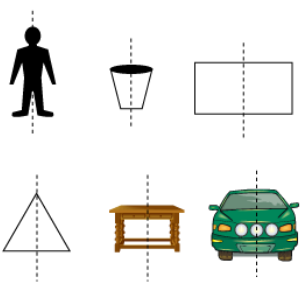
Let us consider the following pictures.
For each picture, let us draw vertical lines exactly at the middle as shown below.
After drawing lines, we can observe that the left half of the pictures is exactly the same as the right half of the pictures. These pictures are known as symmetrical pictures. The line through which the figure is divided is called line of symmetry.
Here, the dotted lines of these pictures are lines of symmetry. If we consider only one-half of these images and place a mirror instead of the dotted line, then we will get a mirror reflection of the image, which will be the missing half of the original image. Thus, we can also say that the two halves obtained by dividing the figure through the line of symmetry are mirror images of each other. For example, the left portion of each image is the mirror image of the right portion of the image and vice-versa.
We come across different objects in our day to day life where symmetry is shown by mirror reflection. For example, if we look at the following picture, we can see the reflected image of the buildings in the water. The water surface acts as a mirror or as a line of symmetry. We can observe the symmetry of the objects by their reflection, though the image is not very clear.
We can also take the example of Rangoli patterns.
There are many lines of symmetry for these types of patterns as shown below. We can observe reflection pattern in the patterns along their lines of symmetry acting as mirror lines.
We can see that in each figure, one half of the pattern is the reflection of the other half.
Let us consider the given figure of ΔPQR on a grid paper, where AB is a mirror line.
Let us draw the image of ΔPQR with reference to the mirror line AB.
Here, ΔPQR and ΔP′Q′R′ are symmetrical with reference to the mirror line AB.
Now, we can say that ΔP′Q′R′ is the mirror image of ΔPQR with reference to the mirror line AB. If we fold the grid paper along the mirror line, then we will observe that the two triangles overlap. It can also be observed that:
The lengths of the sides of ΔP′Q′R′ are equal to the corresponding sides of ΔPQR. • The angles of ΔP′Q′R′ are equal to the corresponding angles of ΔPQR.
Every portion of ΔP′Q′R′ is at the same distance from the mirror line as that of the corresponding portions of ΔPQR.
Now, let us extend the concept of mirror further to study about image of a point. If we place a point in front of a mirror, then what is the nature of the image formed?
Let XY be a mirror. Let A be a point (object) placed in front of it. We obtain its image A′ as shown below:
Can we notice anything in the above figure?
We can notice that:
1. The distance of the image (A′) behind the mirror is same as the distance of the object (A) from it i.e., PA = PA′
2. The mirror line XY is perpendicular to the line joining the object and the image i.e., XY ⊥ AA′
Here, XY (the mirror line) is called the axis of reflection or mediator. What would happen if the point A lies on XY?
If the point A lies on XY, then its image will be this point itself. In such case, A is called an invariant point with respect to mirror line XY.
Reflection of a point in the lines x = a and y = a.
x = a is a line parallel to the y-axis and at a distance of a units from it. If we have to find the reflection of point A(−2, 4) from the line x = 2 we follow the below given steps:
Step 1: Line PQ represents x = 2 which is a straight line parallel to the y-axis and at a distance of 2 units from it.
Step 2: Mark a point A(−2, 4) on the same graph.
Step 3: From the point A, draw a straight line perpendicular to PQ. Mark a point A' behind the straight line PQ at the same distance as A(−2, 4) is before it. A'(6, 4) is the required reflection of the point A(−2, 4) in the line x = 2.
Similarly, we have y = a which is parallel to x-axis and is at a distance of a units from it. Suppose we have to find the reflection of point B(2, 2) from the line y + 2 = 0 we follow the below given steps:
Step 1: Line PQ represents y = − 2 which is a straight line parallel to the x-axis and at a distance of 2 units from it.
Step 3: From the point B, draw a straight line perpendicular to PQ. Mark a point B' below this straight line PQ at the same distance as B(2, 2) is above it. B'(2, −6) is the required reflection of the point B(2, 2) in the line y + 2 = 0.
The mirror reflection of the given figure with respect to mirror line AB can be drawn as
Example 2: The given figure shows a wall with end points A and B. Sanjana is standing at position P. She has to come to position Q after touching the wall. Find the shortest path for Sanjana to come from P to Q.
AnswerLet us imagine that wall AB acts as a mirror. Then P′ is the position of the image of point P. The object and its mirror image are at the same distance from the mirror. Therefore, points P and P′ are at the same distance from the wall.
Therefore, the shortest distance between P′ and Q is P′Q. Let us join the points P′ and Q by a straight line which passes through the wall at point R.
Now, P′Q = P′R + RQ
But PR is the mirror reflection of P`R.
Or we can say that PR = P′R
Therefore, P′Q = PR + RQ
The path from P to R and then from R to Q is the shortest path which should be followed by Sanjana.
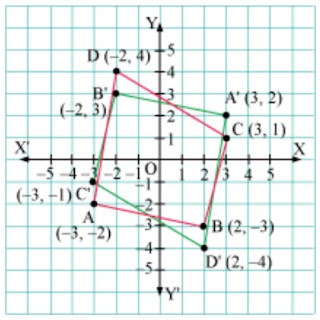
Example 3: The quadrilateral ABCD whose vertices are A (−3, −2), B (2, −3), C (3, 1), and D (−2, 4) is on a co-ordinate plane. Draw its reflection in origin.
Answer
(1) The reflection of the points A (−3, −2), B (2, −3), C (3, 1), and (D (−2, 4) in the origin are:
A’(3, 2),
B’(-2, 3), C’(-3, -1), and D’(2, -4)
By joining A’B’, B’C’, C’D’, and A’D’, we obtain the quadrilateral A'B'C'D', which is the reflection of the given quadrilateral ABCD in the origin as shown below.
Example 4: The line AB joining the points A (−3, −4) and B (2, 1) is on co-ordinate plane. Draw its reflection
(i) A'B' about x-axis
(ii) A" B" about y-axis
Answer
(i) The refection of points A (−3, −4) and B (2, 1) about x-axis are A' (−3, 4) and B' (2, − 1). By joining A'B' , we obtain the reflection of the given line AB as shown below.
(ii) The reflection of points A (−3, −4) and B (2, 1) about y-axis are A" (3, −4) and (− 2, 1).
By joining A"B", we obtain the reflection of the given line AB as shown below.
Section Formula
Bageecha Singh’s garden is rectangular in shape and its length and breadth are 10 m and 20 m respectively. Two lamp posts in the garden are placed at the ends of a diagonal of the garden. Bageecha Singh wants to place one more lamp post between the two lamp posts that will divide the line segment joining the two lamp posts in the ratio 3:5.
Now, can you help him to find the position of the new lamp post? External division of a line segment:
Observe the figure given below.
Here, AB is a line segment and P is a point outside the line segment AB such that A – B – P (or P – A – B). So, it can be said that the point P divides the line segment AB externally in the ratio AB : BP. Point P is known as the point of external division.
Let the coordinates of points A and B be (x1, y1) and (x2, y2) respectively. Also, let the point P divide the line segment AB externally in the ratio m : n then the coordinates of point P are given by the following formula.
Coordinates of P = (mx2 – nx1)/(m – n), (my2 – ny1)/(m – n)
This formula is known as the section formula for external division.
Centroid of a Triangle: If A(x1, y1) B(x2, y2) and C(x3,y3) are the vertices of a ∆ABC, then the centroid of ∆ABC is
G (x, y) = G (x1 + x2 + x3)/3, (y1 + y2 + y3)/3
Let us solve some examples based on the section formula.
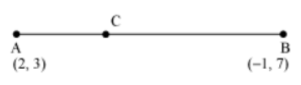
Example 1: Find the coordinates of the point which divides the line segment joining the points (2, 3) and (–1, 7) internally in the ratio 1:2.
Answer
Let (2, 3) and (–1, 7) be denoted by A and B respectively.
Let C be the point that divides the line segment AB internally in the ratio 1:2.
Using section formula, we obtain
Coordinates of C = {1(-1) + 2(2)/(1 + 2), 1(7) + 2(3)/(1 + 2)}
= {(-1 + 4)/3, (7 + 6)/3}
= (3/3, 13/3)
= (1, 13/3)
Thus, (1, 13/3) are the required coordinates of the point.
Thus, are the required coordinates of the point.
Example 2: Find the coordinates of the point which divides the line segment joining the points (4, –5) and (6, 2) externally in the ratio 3:2.
Answer
Let (4, –5) and (6, 2) be denoted by A and B respectively.
Let P be the point that divides the line segment AB externally in the ratio 3:2.
Using section formula, we obtain
Coordinates of P
= {3(6) - 2(4)/(3 – 2), 3(2) – 2(-5)/(3 – 2)}
= (18 – 8)/1, (6 + 10)/1)
= (10, 16)
Thus, (10, 16) are the required coordinates of the point.
Example 3: Find the coordinates of the points of trisection of a line segment joining the points (−2, 1) and (4, –3).
Answer
Let (–2, 1) and (4, –3) be denoted by A and B respectively.
Let C and D be the points of trisection. This means that C divides the line segment AB in the ratio 1 : 2 and D divides the line segment AB in the ratio 2 : 1.
Using section formula, we have
Coordinates of C = {1(4) + 2(-2)/(1 + 2)/(1 + 2), 1(-3) + 2(1)/(1 + 2)
= (4 - 4)/3, (-3 + 2)/3
= (0, -1/3)
and Coordinates of D = {2(4) + 1(-2)}/(1 + 2), 2(-3) + 1(1)/(1 + 2)}
= (8 - 2)/3, (-6 + 1)/3
= (6/3, -5/3)
= (2, -5/3)
Thus, (0, -1/3) and (2, -5/3) are the points of trisection of a line segment joining the points (–2, 1) and (4, –3).
Example 4: The mid-point of a portion of a line that lies in the first quadrant is (3, 2). Find the points at which the line intersects the axes.
Answer
The line has been shown in the following graph:
Let A and B be the points of intersection with y and x-axes respectively.
Let the coordinates of A and B be (0, b) and (a, 0).
Here, C is the mid-point of A and B.
∴ (a + 0)/2, (0 + b)/2 = (3, 2)
(a/2, b/2) = (3, 2)
= (3, 2)
On equating the x and y-coordinates on both sides, we obtain
a/2 = 3 and b/2 = 2
∴ a = 6 and b = 4
Thus, the coordinates of A and B are (0, 4) and (6, 0) respectively.
Slope of a Line
Have you ever wondered why it is difficult to climb a mountain while it is easy to walk down a straight road?
In such cases, we generally use the term ‘slope’ and say that the slope of the mountain is steep.
But do we actually know what slope is and how it is calculated?
Here, we will study about the slopes of straight lines. To understand what we mean by slope, let us first understand what we mean by inclination of a line.
Consider a straight line l, as shown in the figure.
Observe that the line l makes an angle θ with the positive direction of x-axis when measured in the anticlockwise direction. We say that this angle θ is the inclination of the line l.
The angle which a straight line makes with the positive direction of x-axis measured in the anticlockwise direction is called the inclination (or angle of inclination) of the line.- Inclination of a line parallel to y-axis or the y-axis itself is 90°.
- Inclination of a line parallel to x-axis or the x-axis itself is 0°.
Now that we have understood what we mean by inclination, let us now understand the meaning of the slope of a line.
In the above figure, we have seen that the inclination of line l is θ. In this case, we say that tan θ is the slope of line l.
If θ is the inclination of a line l with the positive direction of x-axis, then tan θ is called the slope or gradient of line l. The slope of a line is denoted by m.
For example, the slope of the line which makes an inclination of 45° with the positive direction of x-axis is given by m = tan 45° = 1
Note:
- Since tan θ is not defined for θ = 90°, we say that the slope of a vertical line is not defined. We also conclude that the slope of y-axis is not defined.
- The slope of x-axis is 0.
Now, if we have a line which passes through two given points, then can we find the slope of that line?
Yes, we can find the slope of that line using the formula given below.
If P(x1, y1) and Q(x2, y2) are two points on a non-vertical line l whose inclination is θ, then the slope of line l is given by m = (y2 – y1)/(x2 – x1)
Let us prove this formula.
We have two points P(x1, y1) and Q(x2, y2) on a line l whose inclination is θ as shown in the following figure.
Let us draw perpendiculars from P and Q to X-axis which meet X-axis at A and B respectively.
Also, let us draw PC ⊥ QB.
∴ PC || AB
It can be seen that PQ is transversal with respect to X-axis and PC such that PC || X axis.
Now,
∠QMB = θ (Given)
∠QPC = ∠QMB (Corresponding angles)
∴ ∠QPC = θ
Also, we have
OA = x1 and OB = x2 ∴ AB = x2 – x1
PA = y1 and OB = y2 ∴ QC = y2 – y1
Since AB = PC
∴ PC = x2 – x1
In right-angled triangle ΔPQC, we have
∠QPC = θ
tan θ = (Side opposite to angle θ)/(Side adjacent to angle θ)
⇒ tan θ = QC/PC
⇒ tan θ = (y2 – y1)/(x2 – x1)
Slope of the PQ = Slope of the line l = tan θ
Slope of PQ = Slope of line l = (y2 – y1)/(x2 – x1)
Hence proved.
Using this formula, we can find the slope of any line passing through two distinct points.
For example, the slope of the line passing through the points (3, −7) and (5, 1) is (1 - (-7))/(5 - 3) = 8/2 = 4
Now, we know that if there are two lines in a coordinate plane, then they will be either parallel or perpendicular. In either of the two cases, a relation between the slopes of the two lines is exhibited. The relation is explained as follows:
Two non-vertical lines l1 and l2 are parallel, if and only if their slopes are equal. In other words, if m1 and m2 are the slopes of lines l1 and l2 respectively, then the lines l1 and l2 are parallel to each other, if m1 = m2.
Two non-vertical lines l1 and l2 are perpendicular to each other, if and only if their slopes are negative reciprocals of each other. In other words, if m1 and m2 are the slopes of lines l1 and l2 respectively, then the lines l1 and l2 are perpendicular to each other, if m1m2 = −1.
Now, if we have three points A, B, and C, then we can conclude the following statement:
Three points A, B, and C will lie on a line i.e., they will be collinear, if and only if the slope of AB is the same as the slope of BC.
Let us now look at some examples to understand the concept of slope better.
Example 1: A line l1 passes through points (5, −3) and (4, −6). Another line, l2, passes through points (8, 1) and (2, 3). Are lines l1 and l2 perpendicular, parallel or neither of the two?
Answer
We will first find the slopes of the two lines.
We know that if a line passes through points (x1, y1) and (x2, y2), then the slope of that line is given by m = (y2 – y1)/(x2 – x1)
Thus,
Slope of line l1 is given by
m1 = {(-6) – (-3)}/(4 – 5) = -3/-1 = 3
Slope of line l2 is given by
m2 = (3 – 1)/(2 – 8) = 2/-6 = -1/3
Here, we can observe that m1 m2 = −1. Hence, lines l1 and l2 are perpendicular to each other.
Example 2: The line passing through points (0, 2) and (8, 4) is parallel to the line passing through points (4, 8/5) and (2, p). Find the value of p.
Answer
We know that two lines are parallel if and only if their slopes are equal. The slope of a line passing through points (x1, y1) and (x2, y2) is given by m = (y2 – y1)/(x2 – x1)
Therefore,
Slope of the line passing through points (0, 2) and (8, 4) is given by m1 = (4 – 2)/(8 – 0) = 2/8 = 1/4
Slope of the line passing through points (4, 8/5) and (2, p) is given by
m2 = (p – 8/5)/(2 – 4) = (5p – 8)/(-2 × 5) = (-5p + 8)/10
Since the two lines are parallel,
m1 = m2
⇒ 1/4 = (- 5p + 8)/10
⇒ 10 = -20p + 32
⇒ 5 = - 10p + 16
⇒ 10p = 16 – 5 = 11
⇒ p = 11/10
Thus, the value of p is 11/10.
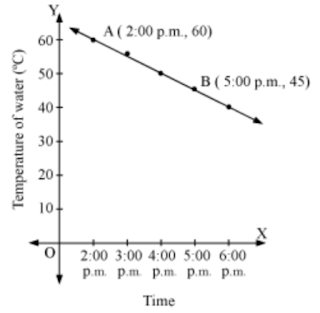
Example 3: The given graph shows the temperature of water, which was kept on fire for some time, at different intervals of time.
What will be the temperature of water at 8 p.m. if it was kept in the same conditions from 2 p.m. to 9 p.m.?
AnswerSince line AB passes through points A (2:00 p.m., 60°C) and B (5:00 p.m., 45°C), its slope is (45 – 60)/(5 – 2) = (-15)/3 = -5
Let y be the temperature of water at 8:00 p.m. Accordingly, on the basis of the given graph, line AB must pass through point C (8:00 p.m., y).
∴ Slope of AB = Slope of BC
⇒ - 5 = (y – 45)/(8 – 5)
⇒ -5 = (y – 45)/3
⇒ -15 = y – 45
⇒ y = - 15 + 45
⇒ y = 30
Thus, the temperature of water will be 30°C at 8:00 p.m.
Slope-Intercept Form of Straight Lines
Slope-intercept Form
If a line with slope m makes y-intercept as c, then the equation of the line is given by y = mx + c.
In other words, we can say that point (x, y) on the line with slope m and y-intercept c lies on the line if and only if y = mx + c.
If a line with slope m makes x-intercept as d, then the equation of the line is given by y = m(x − d).
A general equation Ax + By + C = 0 can be written in slope-intercept form as follows:
y = -(A/B)x – C/B , if B ≠ 0, where m = -(A/B) and C = -(C/B)
x = -(C/A), if B = 0, which is a vertical line whose slope is undefined and whose x-intercept is –(C/A) .
Solved Examples
Example 1: The equation of a line is given by 12x + 8y − 9 = 0. Find the angle made by this line with the positive direction of the x-axis.
Answer
The equation of the line is given by
12x + 8y − 9 = 0
⇒ 8y = 9 − 12x
⇒ y = 9/8 – 12/8.x
⇒ y = 9/8 – 3/2.x
Comparing this equation with the general form y = mx + c, we obtain the slope of the line as
m = -(3/2) = tan θ
Thus, the angle made by the line with the positive direction of the x-axis is tan-1(-3/2).
Example 2: Find the equation of the line that makes x-intercept as 5 and is perpendicular to the line 16x + 4y = 5.
Answer
It is given that the line is perpendicular to the line 16x + 4y = 5.
The slope of this line can be calculated as
4y = −16x + 5
⇒ y = - 4x + 5/4
Thus, the slope of this line is −4. Therefore, the slope of the required line is 1/4. Also, it is given that the line makes x-intercept as 5.
By using the slope-intercept form, we get the required equation of the line as
y = 1/4 (x – 5)
⇒ 4y = x – 5
⇒ x – 4y – 5 = 0
Point-Slope and Two-Point Form of Straight Lines
Point-Slope Form
The equation of a non-vertical line with slope m and passing through the point (x1, y1) is given by (y − y1) = m(x − x1).
In other words, the point (x, y) lies on the line with slope m through the fixed point (x1, y1) if and only if its coordinates satisfy the equation (y − y1) = m(x − x1).
The point-slope form of the equation is used when the information about the slope of the line and a point through which it passes is given.
Two-Point Form
The equation of a non-vertical line passing through two given points (x1, y1) and (x2, y2) is given by (y – y1)/(x – x1) = (y2 – y1)/(x2 – x1).
Solved Examples
Example 1: Find the equation of the line that passes through the points and (−5, 2).
Answer
Using the two-point form of the equation of line, we know that the equation of the line passing through the points (x1, y1) and (x2, y2) is given by (y – y1)/(x – x1) = (y2 – y1)/(x2 – x1)
Thus, the required equation of the line passing through the points (1/3, 1/2) and (−5, 2) is given by
Example 2: Find the equation of the line that passes through the point (8, 5) and makes an inclination of 210° with the x-axis.
Answer
It is given that the line makes an inclination of 210° with the x-axis. Therefore, the slope of the line is given by
m = tan 210° = tan (180° + 30°) = tan 30° = 1/√3
Using point-slope form of equation of line, we know that the equation of the line with slope m that passes through the point (x1, y1) is given by
(y − y1) = m(x − x1)
Thus, the required equation of the line is given by
y – 5 = 1/√3 = (x – 8)
⇒ √3(y – 5) = (x – 8)
⇒ √3y – x - 5√3 + 8 = 0
Example 3: Find the equation of the line that passes through the intersection of lines 2x + y + 6 = 0 and x − y + 9 = 0 and is perpendicular to the line that passes through points (−6, 3) and (4, 5).
Answer
It is given that the required line passes through the intersection of lines 2x + y + 6 = 0 and x − y + 9 = 0.
The points of intersection of lines 2x + y + 6 = 0 and x − y + 9 = 0 can be found by adding the two equations. Hence,
3x + 15 = 0
⇒ x = −5
∴ y = 4
Thus, the required equation passes through the point (−5, 4).
It is also given that the required line is perpendicular to the line that passes through points (−6, 3) and (4, 5).
We know that the slope of a line that passes through points (x1, y1) and (x2, y2) is given by m = (y2 – y1)/(x2 – x1).
Thus, the slope of the line that passes through points (−6, 3) and (4, 5) is given by m = (5 – 3)/(4 + 6) = 2/10 = 1/5
We also know that if two lines are perpendicular to each other, then their slopes are negative reciprocals of each other.
Thus, the slope of the required line is −5.
Thus, we are required to find the equation of the line that passes through the point (−5, 4) having slope −5.
Using point-slope form, the equation of the required line is given by
y − 4 = (−5)(x + 5)
⇒ y − 4 = −5x – 25
⇒ 5x + y + 21 = 0