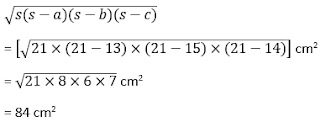ICSE Revision Notes for Circles Class 10 Maths
Chapter Name | Circles |
Topics Covered |
|
Related Study |
Circle and its Attributes
A circle exhibits various interesting properties which make it a special geometric figure.
Let us discuss the same.
Minor and major arc:
An arc less than one-half of the entire arc of a circle is called the minor arc of the circle, while an arc greater than one-half of the entire arc of a circle is called the major arc of the circle.
Semicircular arc:
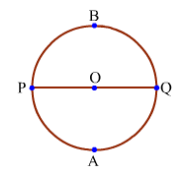
Diameter of a circle divides it into two congruent arcs. Each of these arcs is known as semicircular arc.
In the above figure, PQ is diameter which formed semicircular arcs PBQ and PAQ.
Finding radius of a circle when its diameter is given:
We know that the radius of a circle is half of its diameter.
Let r be the radius and d be the diameter of a circle, then we have r = d/2. Using this formula, we can find the radius of the circle if its diameter is given.
Let us take a look at some examples.
We have to find the radius of the circle when diameter is given.
(i) d = 12 cm
r = d/2
⇒ r = 12/2
⇒ r = 6 cm
(ii) d = 25 cm
r = d/2
⇒ r = 25/2
⇒ r = 12.5 cm
Finding diameter of a circle when its radius is given:
We know that the diameter of a circle is twice its radius.
∴ d = 2r
Using this formula, we can find the diameter of the circle when its radius is given.
Let us take a look at some examples.
We have to find the radius of the circle when diameter is given.
(i) r = 15.5 cm
d = 2r
⇒ d = 2 × 15.5
⇒ d = 31 cm
(ii) r = 13 cm
d = 2r
⇒ d = 2 × 13
⇒ d = 26 cm
Let us discuss some more concepts related to circles.
Circular region: Look at the following circle.
The whole shaded part is the region of this circle.
Thus, the interior and boundary together make the region of the circle.
Concentric circles: Circles of different radii but having the same centre are known as concentric circles.
In the above figure, two circles have the same centre O but the different radii OP and OQ such that OQ > OP. These circles are concentric circles.
Congruent circles: If the radii of two or more circles are equal, then the circles are said to be congruent to each other.
Intersecting circles: Two coplanar circles (circles in the same plane) which intersect each other at two distinct points are known as intersecting circles.
If two coplanar circles intersect each other at only one point, then the circles are known as touching circles.
In each of both the above figure, circles touch each other at only one point P. Thus, circles in each figure are touching circles.
Now, observe the following figure.
Here, OA, OB, OC, ..., OK are all radii of the circle. Similarly, we can draw many more radii of this circle.
So, it can be said that a circle has innumerable radii.
It can be seen that AG, CH, DI and EK all are diameters of the circle. Similarly, we can draw many more diameters of this circle.
So, it can be said that a circle has innumerable diameters.
Also, BC, CD, DE, JK and KA are the chords of the circle. Similarly, many more chords of this circle can be drawn.
Thus, it can be said that a circle has innumerable chords.
Now, observe the following circle.
It can be seen that points P and R divide this circle into two parts or arcs which are coloured differently. The name "arc PR" does not explain that which of two arcs we are talking about. So, we marked a point on each arc to clarify this.
It can be seen that point S is marked on the green arc and point Q is marked on the blue arc. Now, we can give a three letters name to each arc. Thus, green arc can be named as arc PSR or arc RSP whereas blue arc can be named as arc PQR or arc RQP.
Similarly, we can denote any arc by three letters.
Let us discuss some examples to understand this concept better.
Example 1: With respect to the figure drawn below, name
(a) the centre
(b) the diameter
(c) any two radii
(d) a chord
(e) a point lying in the interior of the circle (f) a point lying in the exterior of the circle (g) a sector
(h) a segment
(i) a point lying on the circle
(j) two semi-circles
(k) any two arcs
Answer(a) O is the centre of the circle.
(b)is the diameter of the circle.
(c) Two radii of the circle are and
(e) Q is a point that lies in the interior of the circle.
(f) P is a point that lies in the exterior of the circle.
(g) BOC is a sector of the circle.
(h) AMC is a segment of the circle.
(i) S is a point that lies on the boundary of the circle (or simply, on the circle). (j) The semi-circles in the given figure are ASB and ATB.
(k) BTC and AMC are two arcs of the circle
Example 2: Using ruler and compass, draw circle of radius 5 cm. Mark its centre and draw the radius.
Answer
On using a ruler, first we draw the radius 5 cm of the circle and then assuming O as a centre we draw a circle of radius 5 cm by using a compass. Thus, we get a circle of radius 5 cm as shown below.
Some more Attributes of Circle
Circle is a simple closed curve and it can be defined as follows:
A circle is the locus of points in a plane which are equidistant from a fixed point in the same plane.
The fixed point is called centre of the circle and distance (constant distance) of each point from centre is called radius of the circle.
A circle exhibits various interesting properties which make it a special geometric figure.
Let us discuss the same.
Minor and major arc:
An arc less than one-half of the entire arc of a circle is called the minor arc of the circle, while an arc greater than one-half of the entire arc of a circle is called the major arc of the circle.
Semicircular arc
Diameter of a circle divides it into two congruent arcs. Each of these arcs is known as semicircular arc.
In the above figure, PQ is diameter which formed semicircular arcs PBQ and PAQ.
Secant: A line that meets a circle at two points is called the secant of the circle.
Look at the following figure.
In the figure, a line l intersects the circle at two points i.e., A and B. This line is called the secant to the circle.
Tangent: A line that meets a circle at one and only one point is called a tangent to the circle. The point where the tangent touches the circle is called the point of contact.
Consider the following figure.
What do you observe in this figure?
Here, line PR touches the circle at a point Q. So, line PR is the tangent to the circle and Q is the point of contact.
Inscribed angle: If an angle is inscribed in the arc of a circle such that the vertex of the angle lies on the arc other than its end points and end points of the arc lie on the arms of the angle, then the angle is called inscribed angle.
Observe the following figure.
Intercepted arc: If an angle and an arc of a circle are given such that each arm of the angle contains an end point of the arc and all points of the arc except the end points lies in the interior of the angle, then the arc is said to be intercepted by the angle.
Look at the figures given below:
Now, observe the following figures.
In these figures, angle and arc do not satisfy the conditions given in the definition, so there is no intercepted arc.
Angle subtended by an arc and central angle
If an angle has its vertex on a circle and both of its arms intersect the circle at points other than vertex, then it is said that the angle is subtended by its intercepted arc.
Let us consider the following figure.
Here, ∠PQR intercepts the arc PAR. Thus, it can be said that ∠PQR is subtended by arc PAR at a point Q on the circle.
It can be observed that ∠PQR is inscribed in the arc PQR.
So, it can be said that
The angle subtended by intercepted arc to any point on the circle acts as the inscribed angle for the arc formed by the remaining part of the circle.
Also, the arc PAR subtends ∠POR to the centre.
The angle subtended by an arc to the centre is called central angle. Thus, ∠POR is the central angle in the above figure.
Measures of minor and major arcs
The measure of the central angle corresponding to the minor arc is also the measure of minor arc.
Measure of major arc = 360° – Measure of corresponding minor arc
Observe the following figure.
According to the above figure, we have
Measure of minor arc PAR = Central angle = ∠AOB
Measure of major arc PQR = 360° – Measure of corresponding minor arc = 360° – ∠AOB
Measure of semicircular arc
The measure of a semicircular arc is always 180°.
In the above figure, measure of both the semicircular arcs PBQ and PAQ is 180°. We will now study two terms which relate circles and triangles:
- Circumcircle of a triangle
- Incircle of a triangle
A circle which passes through all the three vertices of a triangle is called the circumcircle of the triangle.
1. Triangle for which the given circle is an incircle.
2. Triangle for which the given circle is a circumcircle.
3. Chord(s) of the given circle and their respective major and minor arcs.
4. Tangent(s) to the given circle.
5. Secant(s) to the given circle.
6. Semicircular arcs
Answer
1. The given circle is an incircle for ΔABC.
2. The given circle is a circumcircle for ΔPQR.
3. Chords of the given circle and their respective major and minor arcs are as follows:
Chord PQ; major arc PRQ and minor arc PLQ
Chord QR; major arc QPR and minor arc QKR
Chord RP; major arc RQP and minor arc RNP
4. Tangents to the given circle are AB, BC and CA.
5. Secant to the given circle is LM.
6. RS is the diameter which forms semicircular arcs SPR (can also be named as SLR and SNR) and SKR
(can also be named as SQR).
Example 2: Observe the following figure.
Find the following attributes from the figure.1. Angle subtended by arc BRC to the circle.
2. Angle subtended by arc APC to the centre.
3. Arc intercepted by ∠BCA.
4. Angle inscribed in arc BQC.
5. Measure of minor arc APC.
6. Measure of major arc ABC.
Answer
1. Angle subtended by arc BRC to the circle = ∠BAC
2. Angle subtended by arc APC to the circle = ∠ABC = x
3. Arc intercepted by ∠BCA = arc BQA
4. Angle inscribed in arc BQC = ∠BAC
5. Measure of minor arc APC = Measure of ∠AOC = y
6. Measure of major arc ABC = 360° – Measure of ∠AOC = 360° – y
Concentric and Congruent Circles, Secant and Tangent
A circle is a simple closed curve. It exhibits various interesting properties which make it a special geometric figure.
Concentric circles:
Circles with the same centre but different radii are called concentric circles.
Congruent circles:
Circles with same radii are called congruent circles.
In the above figure, OA and O¢B are the radii of the circles S1 and S2 such that OA = O¢B = 4.5 cm. Thus, these circles are congruent to each other.Secant:
A straight line, which cuts the circle at two different points, is called secant.
Look at the following figure.
In the figure, line XY intersects the circle at points A and B. This line is called a secant to the circle.
Tangent:
A line that meets a circle at one and only one point is called a tangent to the circle. The point where the tangent touches the circle is called the point of contact.
Tangent is a special case of a secant.
Consider the following figure.
What do you observe in this figure?
Here, line AB touches the circle at point T. Thus, line AB is a tangent to the circle and T is the point of contact.
To understand the concepts better, let us go through some examples.
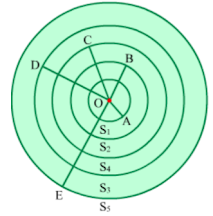
Example 1: Draw 5 concentric circles with radii 2 cm, 3 cm, 4 cm, 5 cm and 6 cm.
Answer
The five circles S1, S2, S3, S4 and S5 with radii OA = 2 cm, OB = 3 cm, OC = 4 cm, OD = 5 cm and OE = 6 cm are shown in the following figure.
Example 2: In the following figure, name the secants and tangents.
AnswerIn the figure, lines A2B2, A3B3 and A5B5 cut the circle at two different points. Therefore, they are secants.
Lines A1B1 and A4B4 meet the circle only at points T1 and T2. Therefore, A1B1 and A4B4 are tangents to the circle.
Example 3: A circle of radius 4.5 cm is given below.
Draw:(ii) a secant on the given circle
(iii) a tangent to the given circle
Answer
(i) Circles having equal radii are congruent circles.
Therefore, a circle congruent to the given circle can be drawn by taking its radius as 4.5 cm.
The required circle is shown below:
(ii) A straight line which cuts the circle at two points is called a secant.
Secant PR can be drawn on the given circle as follows:
(iii) A straight line which touches the circle at one point only is called a tangent.
Tangent LM can be drawn to the given circle as follows:
Relation between Angles Subtended by an Arc at The Centre and anywhere on the Circle
We know that an infinite number of points lie on the circumference of a circle. The portion of circumference between any two such points is known as an arc. Every arc subtends an angle at the centre and a particular angle at any point on the circle.
Let us consider any angle ∠ACB inscribed in the major arc ACB of a circle having centre at point O as shown below.
It can be seen that the arc APB is intercepted by ∠ACB.
Also, the arc APB subtends ∠AOB at the centre. Thus, ∠AOB is the measure of arc APB.
In other words, ∠AOB and ∠ACB are subtended by the same arc APB at the centre O and at any point C on the circle respectively.
There is a relation between ∠AOB (measure of intercepted arc) and ∠ACB (inscribed angle).
In this lesson, we will learn the theorem defining the relation between these two types of angles. We will also solve some examples related to the same.
Relation between the Angles Subtended by an Arc at the Centre and on the Circle
The relation between the angles subtended by an arc at the centre and on the circumference of a circle is known as the central angle theorem.
This relation holds true only when the inscribed angle (i.e., the angle subtended at the circumference) is in the major arc. If, however, the inscribed angle is in the minor arc (as is ∠BPA in the following figure), then its relation with the central angle (i.e., the angle at the centre) is given by the formula:
Inscribed angle = 180° - (Central angle)/2
Verification of the Property
Angle in a Semicircle is a Right Angle
Statement: Angle in a semicircle is a right angle.
Given: A circle with centre O and diameter AB
To prove: ∠ACB = 90°
Proof: We know that the angle subtended by an arc at the centre of a circle is twice the angle subtended by it at the circumference of the circle.
∴ ∠AOB = 2∠ACB
⇒ 2∠ACB = 180° (∵ AOB is a straight line)
⇒ ∠ACB = 90°
Now, AB is the diameter of the circle and it divides the circle into two semicircles. ∠ACB is inscribed in the semicircle. Hence, an angle in a semicircle is a right angle.
Solved Examples
Example 1: Find the value of x in the given circle with centre O and diameter AB.
AnswerWe know that an angle in a semicircle is a right angle.
∴ ∠ACB = 90° (∵ AB is the diameter of the circle)
On using the angle sum property in ΔACB, we get: ∠ACB + ∠CBA + ∠BAC = 180°
⇒ 90° + 60° + x = 180°
⇒ 150° + x = 180°
⇒ x = 180° − 150°
⇒ x = 30°
Example 2: Find the measure of ∠APB in the given circle.
AnswerIn ΔOAB, we have:
OA = OB (Radii of the circle)
⇒ ∠OBA = ∠OAB = 70° (∵ Angles opposite equal sides are equal)
Using the angle sum property in ΔOAB, we get:
∠OAB + ∠OBA + ∠AOB = 180°
⇒ 70° + 70° + ∠AOB = 180°
⇒ 140° + ∠AOB = 180°
⇒ ∠AOB = 180° − 140°
⇒ ∠AOB = 40°
We know that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at the circumference of the circle. In the given circle, arc AB subtends ∠AOB at the centre and ∠APB at the circumference.
So, ∠AOB = 2∠APB
⇒ 40° = 2∠APB
⇒ ∠APB = 40°/2
⇒ ∠APB = 20°
Example 3: Find the measure of ∠POQ in the given circle.
AnswerIn the given circle, ∠OPR = 30° and ∠OQR = 15°.
In ΔOPR, we have:
OP = OR (Radii of the circle)
⇒ ∠ORP = ∠OPR = 30° (∵ Angles opposite equal sides are equal)
Similarly, we can find that ∠ORQ = ∠OQR = 15°
Now, ∠PRQ = ∠ORP + ∠ORQ
⇒ ∠PRQ = 30° + 15°
⇒ ∠PRQ = 45°
We know that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at the circumference of the circle. In the given circle, arc PQ subtends ∠POQ at the centre and ∠PRQ at the circumference.
So, ∠POQ = 2∠PRQ
⇒ ∠POQ = 2 × 45°
⇒ ∠POQ = 90°
Example 4: In the given circle with centre O, chord AB is equal to the radius of the circle. Find the measure of ∠ACB.
AnswerIt is given that chord AB is equal to the radius of the circle.
So, AB = OA = OB (∵ OA and OB are radii of the circle)
Thus, ΔOAB is equilateral.
⇒ ∠AOB = 60° (∵ Each angle of an equilateral triangle measures 60°)
We know that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at the circumference of the circle. In the given circle, arc AB subtends ∠AOB at the centre and ∠ACB at the circumference.
So, ∠AOB = 2∠ACB
⇒ 60° = 2∠ACB
⇒ ∠ACB = 60°/2
⇒ ∠ACB = 30°
Example 5: Find the measure of ∠ACD in the given circle.
AnswerConstruction: Join B to C.
We know that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at the circumference of the circle.
In the given circle, arc AB subtends ∠AOB at the centre and ∠ACB at the circumference.
So, ∠AOB = 2∠ACB
⇒ 100° = 2∠ACB
⇒ ∠ACB = 100°/2
⇒ ∠ACB = 50°
Also, arc BD subtends ∠BOD at the centre and ∠BCD at the circumference.
So, ∠BOD = 2∠BCD
⇒ 120° = 2∠BCD
⇒ ∠BCD = 120°/2
⇒ ∠BCD = 60°
Now, ∠ACD = ∠ACB + ∠BCD
⇒ ∠ACD = 50° + 60°
⇒ ∠ACD = 110°
Angles in the Major and Minor Segments
We know that the chord of a circle divides it into two regions. These regions are called segments of the circle and are classified as the major segment and the minor segment.
Observe the given circle.
In this circle, ∠BAC lies in the major segment whereas ∠BDC lies in the minor segment. It can be seen that ∠BAC is an acute angle while ∠BDC is an obtuse angle.
So, it can be concluded that the angle lying in the major segment is an acute angle and the angle lying in the minor segment is an obtuse angle. This statement is true for all major and minor segments in a circle.
There is no relation between angles in different segments, but what about the angles in the same segment?
In this lesson, we will learn about the angles in the same segment of a circle and the relation between them. We will also solve some examples dealing with the same.
Angles in the Same Segment
Angle for scoring a goal in soccer
The angle of every possible shot to score a goal is constant for all positions on the same arc of a circle; however, the distance of a shot changes with change in position.
Solved Examples
Example 1: In the given circle, chords PQ and RS are equal and chords PS and QR intersect at point T. Show that PT = RT and TQ = TS.
AnswerIn ΔPQT and ΔRST, we have:
PQ = RS(Given)
∠TPQ = ∠TRS (∵ Angles in the same segment of a circle are equal)
Similarly, ∠TQP = ∠TSR
∴ ΔPQT ≅ ΔRST (By the ASA congruence criterion)
⇒ PT = RT and TQ = TS (By CPCT)
Example 2: In the given circle, find the value of ∠DAB if ∠BCA = 80° and DA = DB.
AnswerFrom the figure, we have:
∠BCA = ∠BDA = 80° (∵ Angles in the same segment of a circle are equal) DA = DB (Given)
⇒ ∠DBA = ∠DAB … (1) [∵ Angles opposite equal sides are equal] On using the angle sum property in ΔADB, we get:
∠DAB + ∠DBA + ∠BDA = 180°
⇒ 2∠DAB + 80° = 180° (By equation 1)
⇒ 2∠DAB = 180° − 80°
⇒ 2∠DAB = 100°
⇒ ∠DAB = 50°
Example 3: What is the value of x in the given figure?
AnswerWe know that angles in the same segment are equal.
∴ ∠CAD = ∠CBD = 60°
Now, ∠BDE is an exterior angle of ΔBCD.
So, ∠BDE = ∠CBD + ∠DCB (∵ Exterior angle equals sum of interior opposite angles) ⇒ x = 60° + 40°
⇒ x = 100°
Example 4: What are the measures of ∠BAC, ∠ACD, ∠ABC, and ∠DBC?
AnswerWe know that angles in the same segment are equal.
So, ∠BAC = ∠BDC = 45°
Similarly, ∠ABD = ∠ACD = 40°
On using the angle sum property in ΔABC, we get:
∠ABC + ∠BAC + ∠ACB = 180°
⇒ ∠ABC + 45° + 55° = 180°
⇒ ∠ABC + 100° = 180°
⇒ ∠ABC = 180° − 100°
⇒ ∠ABC = 80°
Now, ∠ABC = ∠ABD + ∠DBC
⇒ 80° = 40° + ∠DBC
⇒ ∠DBC = 80° − 40°
⇒ ∠DBC = 40°
Example 5: In the given circle with centre O, ∠PQR = 37° and ∠QRP = 83°. What are the measures of ∠RSQ and ∠ROQ?
AnswerOn using the angle sum property in ΔPQR, we get:
∠PQR + ∠QRP + ∠RPQ = 180°
⇒ 37° + 83° + ∠RPQ = 180°
⇒ 120° + ∠RPQ = 180°
⇒ ∠RPQ = 180° − 120°
⇒ ∠RPQ = 60°
We know that angles in the same segment are equal.
∴ ∠RPQ = ∠RSQ = 60°
We also know that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at the circumference of the circle.
So, ∠ROQ = 2∠RSQ
⇒ ∠ROQ = 2 × 60°
⇒ ∠ROQ = 120°
Example 6: In the given circle, ∠TQR = 70° and PR is the diameter. If TS||PR, then find the measure
of ∠STR.
Answer
We know that angles in the same segment are equal.
∴ ∠TQR = ∠TPR = 70°
We also know that an angle in a semicircle is a right angle.
∴ ∠RTP = 90° (∵ PR is the diameter)
On using the angle sum property in ΔRTP, we obtain: ∠TPR + ∠RTP + ∠PRT = 180°
⇒ 70° + 90° + ∠PRT = 180°
⇒ 160° + ∠PRT = 180°
⇒ ∠PRT = 20°
Now, PR||TS and RT is the transversal.
So, ∠STR = ∠PRT = 20° (∵ Alternate angles are equal)
Angle in a Semicircle is a Right Angle
Consider the circle given below.
Can we find the measure of ∠PQR?
Observe that a ΔPQR is formed inside the circle. We know that the sum of all the angles in a triangle is 180°.
However, in ΔPQR, we only know the measure of ∠RPQ. Hence, to find the measure of ∠PQR, we must first know the measure of ∠QRP.
Observe that ∠QRP is an angle in a semi-circle.
There is an important theorem related to angle in a semi-circle. It states that
An angle in a semi-circle is a right angle.
Using this theorem, we can say that ∠QRP = 90°
From ΔPQR, we obtain
∠PQR + ∠QRP + ∠RPQ = 180°
⇒ ∠PQR + 90° + 32° = 180°
⇒ ∠PQR = 180° − 90° − 32° = 58°
Thus, we find that the measure of ∠PQR is 58°.
In this manner we use the theorem related to angle in semi-circle to solve various problems.
Let us now solve a few more problems to understand this concept better.
Example 1: In the given figure, ΔPRS is an isosceles triangle in which PS = SR. Find the measure of ∠QRS if ∠QPS = 110° and ∠QPR = 65°.
It is given that ∠QPS = 110° and ∠QPR = 65°. Therefore,
∠RPS = 110° − 65° = 45°
PS = SR [Given]
We also know that the sides opposite to equal angles are equal. Therefore,
∠PRS = ∠RPS
∴ ∠PRS = 45°
We know that the angle in a semi-circle is a right angle.
∴ ∠PQR = ∠PSR = 90°
Consider ΔPQR.
∠PQR + ∠PRQ + ∠QPR = 180° (Using angle sum property of triangles)
⇒ 90° + ∠PRQ + 65° = 180°
⇒ ∠PRQ = 25°
Consider ΔPRS.
∠PRS + ∠PSR + ∠RPS = 180°(Using angle sum property of triangles)
⇒ ∠PRS + 90° + 45° = 180°
⇒ ∠PRS = 45°
Thus, ∠QRS = ∠PRQ + ∠PRS = 25° + 45° = 70°
Properties of Cyclic Quadrilaterals
Cyclic Quadrilaterals
We know that points lying on the same circle are called concyclic points. Let us consider four concyclic points, say E, F, G and H, and the circle passing through them. If we join the four points, then we get a quadrilateral as is shown in the figure below.
A quadrilateral whose vertices lie on a circle or through whose vertices it is possible to draw a circle is known as a cyclic quadrilateral. In the given figure, the vertices E, F, G and H lie on a circle; hence, EFGH is a cyclic quadrilateral. The circle on which the quadrilateral lies is called a circumcircle.
Cyclic quadrilaterals are a little different from regular quadrilaterals as they exhibit a few special properties. In this lesson, we will discuss these properties of cyclic quadrilaterals and solve some problems based on them.
Did You Know?
If a cyclic quadrilateral has unequal rational sides in either arithmetic or geometric progression, then there does not exist any cyclic quadrilateral with rational area.
Know More
A cyclic quadrilateral is also called chordal quadrilateral because the sides of the quadrilateral are chords of the circumcircle. Another name for this quadrilateral is concyclic quadrilateral.
If the opposite sides of a cyclic quadrilateral are extended to meet, say at points E and F, then the internal angle bisectors of the angles formed at points E and F are perpendicular.
The opposite sides and the diagonals of a cyclic quadrilateral ABCD are related as: AC.BD = AD.BC + AB.CD. This relationship is known as Ptolemy’s theorem.
The area of a cyclic quadrilateral is, where a, b, c and d are the lengths of the sides of the cyclic quadrilateral and s = (a + b + c + d)/2.
Whiz Kid
In a cyclic quadrilateral ABCD with circum centre O, if the diagonals AC and BD intersect at point P, then ∠APB is the arithmetic mean of ∠AOB and ∠COD.
Four line segments are concurrent if each is perpendicular to one side of a cyclic quadrilateral and passes through the midpoint of the opposite side. These line segments are called maltitudes, which means ‘midpoint altitudes’.
Proving the Converse of Property
Statement: If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Given: A quadrilateral ABCD with ∠ABC + ∠ADC = 180° and ∠BAD + ∠BCD = 180°
To prove: ABCD is a cyclic quadrilateral.
Proof: Let us assume that ABCD is not a cyclic quadrilateral. Suppose a circle passes through the three non-collinear points A, B and C and meets AD or AD produced, at D′.
Now, on joining D′ to C, we get the cyclic quadrilateral ABCD′.
In ABCD′, we have:
∴∠ABC + ∠AD′C = 180° (∵ Opposite angles of a cyclic quadrilateral are supplementary)
But ∠ABC + ∠ADC = 180° (Given)
∴ ∠AD′C = ∠ADC, which can be possible only if D and D′ coincide
Thus, the circle passing through points A, B and C also passes through point D. Therefore, ABCD is a cyclic quadrilateral.
Exterior Angle of a Cyclic Quadrilateral is Equal to the Interior Opposite Angle
Statement: The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
Given: A cyclic quadrilateral PQRS with side SR extended up to point T
To prove: ∠QRT = ∠QPS.
Proof: We know that the opposite angles of a cyclic quadrilateral are supplementary.
∴ ∠QPS + ∠QRS = 180° …(1)
Also, ∠QRT + ∠QRS = 180°…(2) [Linear pair of angles]
From equations (1) and (2), we obtain:
∠QPS + ∠QRS = ∠QRT + ∠QRS
⇒ ∠QPS = ∠QRT
Solved Examples
Example 1: What is the measure of ∠ADC in the given figure?
AnswerIn the figure, ∠CAD = ∠CBD = 45°
We know that if a line segment joining two points subtends equal angles at two other points lying on the same side of the line segment, then the four points are concyclic.
Therefore, A, B, C and D are concyclic points and ABCD is a cyclic quadrilateral.
We know that in a cyclic quadrilateral, opposite angles are supplementary.
So, ∠ABC + ∠ADC = 180°
⇒ (40° + 45°) + ∠ADC = 180°
⇒ 85° + ∠ADC = 180°
⇒ ∠ADC = 180° − 85°
⇒ ∠ADC = 95°
Example 2: In ΔAEB, AE = BE. A circle passing through points A and B intersects AE and BE at points D and C respectively. Prove that the line segment DC is parallel to AB.
Answer
The figure for the given problem can be drawn as is shown.
In ΔAEB, we have:
AE = BE (Given)
⇒ ∠EBA = ∠EAB... (1) [∵ Angles opposite equal sides of a triangle are equal]
Now, ABCD lies on a circle; so, it is a cyclic quadrilateral. We know that the exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
So, ∠EDC = ∠CBA
⇒ ∠EDC = ∠EBA ...(2) [∵∠CBA = ∠EBA]
From equations (1) and (2), we obtain:
∠EDC = ∠EAB
We can see that line segments DC and AB are cut by the transversal EA. ∠EDC and ∠EAB are equal corresponding angles. Therefore, by the converse of the corresponding angles axiom, we can say that DC is parallel to AB.
Example 3: Find the values of x and y in the given figure.
AnswerIn the figure, we have two cyclic quadrilaterals ABEF and BCDE.
In ABEF, we have:
∠BAF + ∠BEF = 180° (∵ Opposite angles of a cyclic quadrilateral are supplementary)
⇒ 95° + y = 180°
⇒ y = 180° − 95°
⇒ y = 85°
In BCDE, we have:
∠BEF = ∠BCD (∵ Exterior angle of a cyclic quadrilateral equals interior opposite angle)
⇒ y = x
⇒ x = 85°
Example 4: What is the measure of ∠PSR in the given figure?
AnswerWe know that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at the circumference of the circle.
So, ∠POR = 2∠PQR
⇒ ∠PQR = 1/2∠POR
⇒ ∠PQR = 1/2 × 150°
⇒ ∠PQR = 75° …(1)
Now, quadrilateral PQRS is cyclic.
So, ∠PQR + ∠PSR = 180° (∵ Opposite angles of a cyclic quadrilateral are supplementary)
⇒ 75° + ∠PSR = 180° (By equation 1)
⇒ ∠PSR = 180° − 75°
⇒ ∠PSR = 105°
Example 5: In the given figure, find the value of ∠BEF if BF is the bisector of ∠CBE.
In ΔOAC, we have:
OA = OC (Radii of the circle)
⇒ ∠OCA = ∠OAC = 20° (∵ Angles opposite equal sides of a triangle are equal)
On using the angle sum property in ΔOAC, we obtain:
∠AOC + ∠OAC + ∠OCA = 180°
⇒ ∠AOC + 20° + 20° = 180°
⇒ ∠AOC + 40° = 180°
⇒ ∠AOC = 180° − 40°
⇒ ∠AOC = 140°
We know that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at the circumference of the circle.
So, ∠AOC = 2∠ADC
⇒ ∠ADC = 1/2.∠AOC
⇒ ∠ADC = 1/2 × 140°
⇒ ∠ADC = 70°
Since ABCD is a cyclic quadrilateral, we have:
∠CBE = ∠ADC (∵ Exterior angle of a cyclic quadrilateral equals interior opposite angle)
⇒ ∠CBE = 70°
It is given that BF bisects ∠CBE.
So, ∠EBF = 1/2 ∠CBE
⇒ ∠EBF = 1/2 × 70°
⇒ ∠EBF = 35°
On using the angle sum property in ΔBEF, we obtain:
∠EBF + ∠BEF + ∠BFE = 180°
⇒ 35° + ∠BEF + 90° = 180°
⇒ ∠BEF + 125° = 180°
⇒ ∠BEF = 180° − 125°
⇒ ∠BEF = 55°
Example 6: If points A, B, C and D divide the circumference of the given circle into four equal parts, then show that ABCD is a square.
Answer:It is given that points A, B, C and D divide the circle into four equal parts.
∴ Arc AB = Arc BC = Arc CD = Arc DA
We know that if the arcs in a circle are congruent, then their corresponding chords are equal.
∴ Chord AB = Chord BC = Chord CD = Chord DA
Thus, all sides of quadrilateral ABCD are equal in length. Therefore, ABCD is a rhombus.
Points A, B, C and D are concyclic; so, ABCD is a cyclic quadrilateral. Now, we know that in a cyclic quadrilateral, opposite angles are supplementary. So, ∠BAD + ∠BCD = 180°
But ∠BAD = ∠BCD (∵ Opposite angles of a rhombus are equal)
⇒ 2∠BAD = 180°
⇒ ∠BAD = 90°
Similarly, ∠ABC, ∠BCD and ∠CDA measure 90°.
Hence, ABCD is a square.
Concept of Tangent at any Point of the Circle
The theorem about tangents states that:
A tangent at any point of a circle is perpendicular to the radius through the point of contact.
In the above figure O is the centre of circle, line l is the tangent and P is point of contact.
∴ l ⊥ OP
Proof:
It is given that O is the centre of the circle, l is the tangent to this circle and P is the point of contact.
Let us assume l is not perpendicular to the radius of the circle.
In this case, let us draw perpendicular OA to tangent l. Thus, point A is distinct from point P.
Let B be any point on tangent such that BAP is a line and BA = AP. Now, in ΔOAB and ΔOAP, we have
OA = OA (Common side)
∠OAB = ∠OAP (OA ⊥ tangent l)
BA = AP (By construction)
∴ ΔOAB ΔOAP
∴ OB = OP (By CPCT)
Since OB = OP, point B also lies on the circle.
Also, point B is different from point P.
Thus, tangent l touches the circle at two distinct points. This contradicts the definition of tangent.
Hence, our assumption is wrong.
Therefore, tangent l ⊥OP.
Hence proved.
The converse of this theorem is also true which states that:
The line perpendicular to the radius of a circle at its outer end is tangent to the circle.
Proof:
Let O be the centre of the circle, OP be the radius and l be the line perpendicular to OP such as it passes through point P on the circle.
Also, let A be any point on line l distinct from P.
From the figure, it can be observed that ΔOAP is a right angled triangle.
∴ OA is hypotenuse for ΔOAP.
∴ OA > OP (Radius)
∴ OA is not radius.
∴ Point A does not lie on the circle.
∴ No point of line l other than P lies on the circle.
∴ P is the only point common to the circle and line l.
∴ Line l is tangent to the circle at point P.
Hence proved.
Let us now solve some examples related to the tangents of the circle.
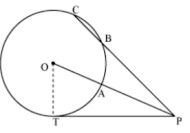
Example 1: Draw a circle with centre O, and two lines such that one is a tangent and other is a secant.
Answer
The figure can be drawn as follows.
Here,is the secant, which intersects the circle at C and D and is a tangent whose point of contact with the circle is P.
Example 2: Which of the following statements are correct?
(i) There can be only one tangent at a point on the circle.
(ii) Diameter is also a secant of the circle.
Answer
(i) Correct
(ii) Incorrect
Example 3: A line XY is a tangent of the circle with centre O and radius 6 cm. The point of contact is P, and Q is any point on the tangent XY. If OQ = 10 cm, then what is the length of PQ?
Answer
The figure can be drawn as follows.
We know that the radius through the point of contact is perpendicular to the tangent.
∴ OP⊥ XY
Using Pythagoras theorem in right-angled triangle OPQ, we obtain
(OQ)2 = (OP)2 + (PQ)2
⇒ (PQ)2 = (OQ)2 – (OP)2
⇒ (PQ)2 = (10)2 – (6)2
⇒ (PQ)2 = 100 – 36
⇒ (PQ)2 = 64
⇒ PQ = 8 cm
Thus, the length of PQ is 8 cm.
Example 4: Two tangents XY and PQ are drawn at the ends of a diameter AB of the circle with centre O. Show that XY ∥ PQ.
Answer
The figure can be drawn as follows.
XY is a tangent at A and OA is the radius.
We know that the radius through the point of contact is perpendicular to the tangent.
∴ XY⊥OA
⇒ XY⊥AB …(1)
Similarly, PQ ⊥ AB …(2)
Now, the lines perpendicular to the same line are parallel.
∴ From equations (1) and (2), we obtain
XY || PQ
Hence, proved
Example 5: A circle is inscribed in a triangle such as it touches all the three sides of the triangle. Prove that the area of the triangle is half the product of its perimeter and the radius of circle.
Answer
Let O be the centre of the circle inscribed in ΔABC.
It can be seen that AB, BC and CA are tangents which touches the circle at P, Q and R respectively.
Also, OP, OQ and OR are the radii of the circle.
We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, AB ⊥ OP, BC ⊥ OQ and CA ⊥ OR.
Let s be the perimeter of ΔABC.
∴ s = AB + BC + CA
Now,
Area of ∆OAB = 1/2(AB × OP) = 1/2 (AB × r)
Area of ∆OBC = 1/2(BC × OQ) = 1/2(BC × r)
Area of ∆OCA = 1/2(CA × OR) = 1/2(CA × r)
∴ Area of ∆ABC = Area of ∆OAB + Area of ∆OBC + Area of ∆OCA
⇒ Area of ∆ABC = 1/2(AB × r) + ½(BC × r) + 1/2(CA × r)
⇒ Area of ∆ABC = ½.r (AB + BC + CA)
⇒ Area of ∆ABC = ½ rs
Hence proved.
Example 6: Observe the given figure.
Find the angle between radii.Answer
In the given figure, O is the centre of the circle and OP and OR are the radii. Also, QP and SR are the tangents to the circle at points P and R respectively which intersect each other at point A.
It is given that,
∠PAS = 110°
We need to find the angle between radii OP and OR i.e., ∠POR.
From the figure, we have
∠PAS + ∠PAR = 180°
⇒ 110° + ∠PAR = 180°
⇒ ∠PAR = 180° – 110°
⇒ ∠PAR = 70°
We know that a tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, QP ⊥ OP and SR ⊥ OR.
∴ ∠APO = 90° and ∠ARO = 90°
Now, in quadrilateral APOR, we have
∠POR +∠APO + ∠ARO + ∠PAR = 360° (By angle sum property of quadrilaterals)
⇒ ∠POR + 90° + 90° + 70° = 360°
⇒ ∠POR + 250° = 360°
⇒ ∠POR = 110°
Thus, the angle between the radii is 110°.
Tangents drawn from an External Point to a Circle
There is a very important theorem related to tangents to circle drawn from an external point which states that:
The lengths of the two tangent segments to a circle drawn from an external point are equal.
Proof:
Let P be the point outside the circle having centre O from which the tangents PQ and PR are drawn touching the circle at Q and R respectively.
We have to prove that PQ = PR.
From the figure, it can be observed that OQ and OR are the radii of the circle.
Therefore, ∠PQO = ∠PRO = 90°
Now, in ΔPOQ and ΔPOR, we have
∠PQO = ∠PRO = 90°
PO = PO (Common hypotenuse)
OQ = OR (Radii of same circle)
Using RHS (Right-Hypotenuse-Side) congruence rule, we get
ΔPOQ ≅ ΔPOR
∴ PQ = PR (By CPCT)
Thus, the lengths of the two tangent segments to a circle drawn from an external point are equal.
Note: Since ΔPOQ ≅ ΔPOR, we have
∠OPQ = ∠OPR (By CPCT)
∠POQ = ∠POR (By CPCT)
Thus, the above theorem can be extended as,
(1) The tangents drawn to a circle from an external point are equally inclined to the line joining the external point and the centre.
(2) The tangents drawn to a circle from an external point subtend equal angles at the centre.
Now, let us solve some examples to understand the concept.
Example 1: In the given figure, prove that TL + AL = TM + AM
Answer
Example 2: A circle is circumscribed by a quadrilateral PQRS such that the circle touches all the sides of quadrilateral PQRS at points A, B, C, and D respectively. Show that
PQ + RS = QR + PS
Answer
The figure can be drawn as follows.
Now, applying the theorem “The tangents drawn from an external point to the circle are equal in length”, we obtain
Therefore,
PQ + RS = (PA + QA) + (RC + SC)
= (PD + QB) + (RB + SD) [Using (i)]
= (PD + SD) + (QB + RB)
= PS + QR
Thus, PQ + RS = PS + QR
Hence, proved
Example 3: A circle is inscribed in a triangle ABC such that the circle touches the sides AB, BC, and AC of the triangle at P, Q, and R respectively. What are the lengths of AP, BQ, and CR if AB = 10 cm, BC = 6 cm, and AC = 12 cm.
Answer
The figure can be drawn as follows.
Let AP = x cm, BQ = y cm, and CR = z cm.
Now, applying the theorem “The tangents drawn from an external point to the circle are equal in length”, we obtain
AP = AR = x
BQ = BP = y
CR = CQ = z
Therefore, we can write
AP + BP = AB
⇒ x + y = 10 cm …(i)
BQ + QC = BC
⇒ y + z = 6 cm …(ii)
CR + AR = AC
⇒ z + x = 12 cm …(iii)
On adding (i), (ii), and (iii), we obtain
2x + 2y + 2z = 28 cm
⇒ x + y + z = 14 cm … (iv)
Subtracting (i) from (iv), we obtain
(x + y + z) – (x + y) = 14 – 10
⇒ z = 4 cm
Similarly, subtracting (ii) and (iii) respectively from (iv), we obtain
(x + y + z) – (y + z) = 14 – 6
⇒ x = 8 cm
(x + y + z) – (z + x) = 14 – 12
⇒ y = 2 cm
Thus, AP = 8 cm, BQ = 2 cm, and CR = 4 cm
Example 4: In the given figure, PQR is an isosceles triangle with PQ = PR. A circle, which is inscribed in ΔPQR, touches the sides of the triangle at A, B, and C. Show that AQ = AR.
AnswerIt is given that PQR is an isosceles triangle where
PQ = PR …(i)
Now, the tangents drawn from an external point to a circle are equal in length.
∴ PC = PB (ii)
On subtracting equation (ii) from equation (i), we obtain
PQ – PC = PR – PB
QC = RB …(iii)
Now, QA and QC are tangents to the circle from point Q.
∴ QA = QC
Similarly, RB = RA
Using the above relations in equation (iii), we obtain
QA = RA
∴ AQ = AR
Example 5: PA and QA are tangents drawn to a circle with centre O. Show that ∠BOQ = ∠PAQ.
AnswerJoin O with A, P with Q.
We know that, the tangents drawn to a circle from an external point are equal and they are equally inclined to the line joining the external point and the centre.
Therefore, ∠PAO = ∠QAO and ∠POA = ∠QOA.
It is clear that PQ ⊥ OA.
Now, ∠BOQ = 2∠OPQ … (1)
[Angle subtended by an arc at the centre is twice the angle subtended by the same arc at anywhere on the Circle]
Let ∠PAO = ∠QAO = θ.
In ΔPMA,
∠PMA + ∠APM + ∠PMA = 180°
⇒ θ + ∠APM + 90° = 180°
⇒ ∠APM = 90° - θ
⇒ 90° - ∠OPM = 90° - θ
⇒ ∠OPM = θ ...(2)
From (1) and (2), ∠BOQ = 2θ.
Therefore,
∠PAQ = θ + θ = 2θ
⇒ ∠PAQ = ∠BOQ
Hence, the result is proved.
Relation between the Centres of a Circle and the Point of Contact when they touch each other
Two circles of radius 8 cm and 5 cm touch each other. What is the distance between their centres, if they touch
(i) externally
(ii) internally
The above given situations can be represented with the help of figures as shown below:
Here, O and O' are the centres of the circles having radii 8 cm and 5 cm respectively that touch each other at P.
i.e., OP = 8 cm and OP' = 5 cm
We have to find O'O for each situation.
For this, we have to know the relation between the centres of two circles and the point of contact, when they touch each other.
This can be stated in the form of a theorem as:
If two circles touch, then the point of contact lies on the straight line joining the centres.
OR
If two circles touch, then the point of contact and the centres of the circles are collinear.
Using this theorem for the given figures, we can say that P lies on O'O i.e., O, P, and O' lie on a straight line.
Therefore, clearly from the above figure,
Distance between the centres of the circles when they touch externally = O'O = OP + O'P = 8 cm + 5 cm = 13 cm
And, distance between the centres of the circles when they touch internally = O'O = OP − O'P = 8 cm − 5 cm = 3 cm
Hence, we can say that:
If r1 and r2 be the radii of bigger and smaller circles respectively and d be the distance between their centres, then
(i) d = r1 + r2, when they touch externally
(ii) d = r1 − r2, when they touch internally
In order to understand the above concepts better, let us solve some more examples.Answer
Let A, B, and C be the centres of the circles of radii 6 cm, 7 cm, and 8 cm, touching each other externally at the points P, Q, and R respectively.
∴ AB = AP + BP = 6 cm + 7 cm = 13 cm (Let a)
BC = BQ + CQ = 7 cm + 8 cm = 15 cm (Let b)
AC = AR + CR = 6 cm + 8 cm = 14 cm (Let c)
We will find the area of ΔABC using Heron’s formula.
Now,
s = (a + b + c)/2 = (13 cm + 15 cm + 4 cm)/2 = 21 cm
Therefore area of ∆ABC =
Example 2: Two circles touch each other externally. If the distance between their centres is a2 + b2 and the length of the common tangent to them is a2 − b2(where a > b), then find the radii of the circles in terms of a and b.
Answer
Let O and O' be the centres of the circles having radii x and y respectively that touch externally at a point P i.e., OP = x and O'P = y. Let AB be the common tangent to these circles. Let us draw O'Q ⊥ OA
It is given that:
AB = a2 − b2
O’O = a2 + b2
⇒ OP + O’P = a2 + b2
⇒ x + y = a2 + b2 ...(1)
We also have:
OA = OP = x and O'B = O'P = y
Since AB is a tangent to both circles, ∠OAB = 90°
Since, O'A ⊥ OA, ∠OQO' = 90°
∴ ∠OAB = ∠OQO′
⇒ AB ∥ QO'
Therefore, ABO′Q is a parallelogram.
∴ O'Q = AB = a2 − b2
Using Pythagoras Theorem for ΔO'OQ , we obtain
OQ2 + O’Q2 = OO’2
⇒ OQ2 = OO’2 – O’Q2 = (a2 + b2)2 – (a2 – b2)2
⇒ OQ2 = 4a2b2
⇒ OQ = 2ab
⇒ OA – AQ = OA – O’B = 2ab (ABO’Q is a parallelogram)
⇒ x – y = 2ab ...(2)
Adding equations (1) and (2), we obtain
2x = a2 + b2 + 2ab = (a + b)2
⇒ x = 1/2(a + b)2
Subtracting equation (2) from equation (1), we obtain
2y = a2 + b2 – 2ab = (a – b)2
⇒ y = 1/2(a – b)2
Therefore, the radii of the circles are 1/2(a + b)2 and 1/2(a - b)2.
Relation between Length of Segments of Two Chords when they intersect internally or externally
In the following figure, two secants AB and CD intersect externally at point P. If AP = 9 cm, AB = 7 cm, PC = 8 cm, then what is the measure of CD?
In the above figure, two secants AB and CD intersect each other externally at a point P. Now, PA, PB, PC, and PD are the segments of secants AB and CD. We can find length of CD by subtracting length of PC from PD. Therefore, first of all, we have to find out the length of PD. For this, we have to know the relation between the length of the segments PA, PB, PC, and PD.
We can state this in the form of a theorem as follows:
If two secants of a circle intersect internally or externally, then the product of the lengths of segments are equal.
It can be easily understood with the help of the following figure:
According to the above theorem, for each of the above figures,
PA.PB = PC.PD
At some places this theorem is stated as follows:
If two secants of a circle intersect each other inside or outside the circle, then the area of the rectangle formed by the two line segments corresponding to one secant is equal to the area of the rectangle formed by the two line segments corresponding to the other secant.
So, do not get confuse with the statement as both tell about the same theorem.
Let us solve the given question using this theorem.
We have PA = 9 cm, AB = 7 cm, PC = 8 cm
∴ PB = PA + AB = 9 cm + 7 cm = 16 cm
We know that,
PA.PB = PC.PD
⇒ 9 cm × 16 cm = 8 cm × PD
⇒ PD = [9 × 16]/8 cm = 18 cm
∴ CD = PD − PC = (18 − 8) cm = 10 cm
In this way, we can solve a problem related to length of segments of secants when they intersect internally or externally.
In order to understand the above concept better, let us discuss some examples.
Example 1: In the following figure, O is the centre of the circle. OM = 4 cm, ON = 3 cm, and PC = (4 - 2√2) cm. Find the length of PA and PB, if the radius of the circle is 5 cm.
AnswerLet us join OA and OD.
In the above figure, OM ⊥ AB and ON ⊥ CD
Using Pythagoras Theorem for triangles OAM and ODN, we obtain
OA2 = AM2 + OM2 and OD2 = ON2 + DN2
∴ AB = 2 AM = 2 × 3 cm = 6 cm
CD = 2 DN = 2 × 4 cm = 8 cm
Since CP = (4 - 2√2) cm
PD = CD − PC = (8 - (4 - 2√2)]cm = (4 + 2√2) cm
Let PA = x cm
Since AB = 6 cm,
PB = (6 − x) cm
In the given figure, we can observe that the chords AB and CD intersect each other at point P.
Since chords are parts of secants, we can apply the property of secants here.
∴ PA . PB = PC.PD
⇒ x(6 – x) = (4 - 2√2)(4 + 2√2)
⇒ 6x – x2 = (4)2 – (2√2)2
= 16 – 8
= 8
⇒ x2- 6x + 8 = 0
⇒ x2 – 2x – 4x + 8 = 0
⇒ x(x – 2)(x – 4) = 0
⇒ (x – 2)(x – 4) = 0
⇒ x = 2 or 4
If x = 2, then PA = 2 cm and PB = (6 − 2) cm = 4 cm
(It is not possible since PA > PB)
If x = 4, then PA = 4 cm and PB = (6 − 4) cm = 2 cm
∴ PA = 4 cm and PB = 2 cm
Example 2: In the following figure, if XP = XR, then show that QP = SR and ΔXQS is an isosceles triangle.
AnswerIn the given figure, the secants PQ and RS intersect externally at a point X.
∴ XP. XQ = XR . XS
⇒ XP. XQ = XP. XS (XP = XR)
⇒ XQ = XS
Therefore, ΔXQS is isosceles.
We have XQ = XS and XP = XR
∴ XQ − XP = XS − XR
⇒ PQ = RS
Alternate Segment Theorem
Let us look at the figure given below.
In the above figure, O is the centre of the circle. P, Q, R, and S are four points on it. At point P, is a tangent and PR is a chord to the circle.
Here, the segment formed by the arc RSP is called alternate segment to ∠RPT. In this case, ∠RSP is called an angle in the alternate segment of ∠RPT.
In geometry, there is a relation between ∠RPT and ∠RSP. Do you know what that relation is?
The relation between ∠RPT and ∠RSP is ∠RPT = ∠RSP
This is the relation between “the angle between the tangent and the chord” and “angle in the corresponding alternate segment”.
We can state this statement in the form of a theorem as:
If a line touches a circle and a chord is drawn from the point of contact, then the angle between the tangent and the chord are respectively equal to the angles in the corresponding alternate segments.
This theorem is called alternate segment theorem.
In the figure drawn above, if we join PQ and RQ, then using this theorem, we can also say that ∠RPT' = ∠RQP
If a line is drawn through the point of contact of a circle and its chord such that the angle between the chord and the line is equal to the angle subtended by the chord in the alternate segment then the line is tangent to the circle.
Proof:
Let PQ be the chord of the circle, AB be the line touching the circle at P and ∠QPA = ∠PRQ. Here, ∠PRQ is the angle subtended by the chord PQ at point R in the alternate segment.
Let us assume that AB is not the tangent at point P and draw the tangent A'B' touching the circle at point P.
Since A'B' is tangent and PQ is the chord, we have
∠QPA' = ∠PRQ ...(1)
But ∠QPA = ∠PRQ ...(2)
From (1) and (2), we get
∠QPA' = ∠QPA
∴ Line A'B' coincides with line AB.
∴ Line AB is tangent to the circle at point P.
Hence, the theorem holds true.
Let us look at some examples in order to understand the concept better.
Example 1: In the following figure, two circles touch internally at a point A. Prove that:
AB.DE = AD.BC
In the above figure, for the inner circle, A is a point on the circle. T'AT is a tangent through point A and AB is a chord to this circle at point A.
∴ ∠BAT = ∠ADB …(1)
Similarly, we can prove that
∠CAT = ∠AEC …(2)
However, ∠BAT = ∠CAT
⇒ ∠ADB = ∠AEC [Using equations (1) and (2)]
But these are corresponding angles to the lines BD and CE whereas AE is the transversal.
∴ BD||CE
In ΔACE, B and D are the points on sides AC and AE respectively and BD||CE
∴ AB/BC = AD/DE
⇒ AB.DE = AD.BC
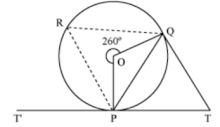
Example 2: In the following figure, O is the centre of the circle and is a tangent to it. If ∠PQT = 75°, then find the measure of ∠QTP.
Answer
Let us mark a point R on the major segment QP of the circle and join PR and QR.
Now, reflex ∠POQ = 360° − 260° = 100°
∠PRQ = 1/2 reflex ∠POQ = 1/2 × 100° = 50°
In the given circle, P is a point on it. T'PT is a tangent and PQ is a chord to the circle.
∴ ∠QPT = ∠PRQ
⇒ ∠QPT = 50°
Using angle sum property for ΔPQT, we obtain
∠QPT + ∠PQT + ∠QTP = 180°
⇒ 50° + 75° + ∠QTP = 180°
⇒ ∠QTP = 180° − 125° = 55°
Relation between the Length of the Segments of a Chord and a Tangent to a Circle Drawn from an Exterior Point
In the following figure, AX is a tangent drawn from an exterior point X to the point on circle such that AX = 12 cm. If BX = 9 cm, then what is the length of the BC?
In the above figure, we observe that the secant BC and tangent through point A to the circle intersect externally at point X.
To find length of BC, we have to know the relation between the lengths of segments of the secant BC and tangent AX.
This can be stated in the form of a theorem as:
This can be clearly understood with the help of a figure given below:
PT2 = PA × PB
This theorem can be stated differently as follows:
If a secant and a tangent intersect at a point outside the circle, then the area of the square formed by the line segment corresponding to the tangent is equal to the area of the rectangle formed by the two line segments corresponding to the secant.
Using this theorem, let us find the length of BC.
We have BX = 9 cm and AX = 12 cm
Now, AX2 = BX × CX
⇒ (12 cm)2 = 9 cm × (9 cm + BC)
[CX = BX + BC = 9 cm + BC]
⇒ 9 cm + BC = 16 cm
⇒ BC = 16 cm − 9 cm = 7 cm
In order to understand the above concept better, let us solve some examples.
Example 1: In the following figure, AC is a tangent to the circle and B is a point on the circle.
If AB and AC are in the ratio 2:5, then find the value of the expression (AX/CY) × (AP/CP) .Answer
We have,
AB/AC = 2/5
⇒ AB/BC = 2/3
Now, tangent AB and secant PX of the circle intersect each other externally at the point A.
Therefore,
AX × AP = AB2 …(1)
Similarly, CY × CP = BC2 …(2)
Therefore,
(AX.AP)/(CY.CP) = AB2/BC2
⇒ (AX/CY) × (AP/CP) = (AB/BC)2
= (2/3)2
= 4/9
Example 2: In the following figure, O is the centre of the circle and PT is a tangent to it.
If PB = 12.5 cm, BC = 5.5 cm, and OP = 17 cm, then what is the length of AP?Answer
We have PB = 12.5 cm and BC = 5.5 cm
∴ PC = PB + BC = (12.5 + 5.5) cm = 18 cm
In the given figure, tangent PT through the point T and secant CB of the circle intersect externally at the point P.
∴ PT2 = PB. PC
⇒ PT2 = 12.5 cm × 18 cm = 225 cm2
⇒ PT = 15 cm
Now, let us join OT.
Since PT is a tangent and OT is the radius to the circle,
∠OTP = 90°
Now, using Pythagoras Theorem for ΔOPT, we obtain
OP2 = OT2 + PT2
⇒ OT2 = OP2 − PT2 = (17 cm)2 − (15 cm)2 = 64 cm2
⇒ OT = 8 cm
Now, OA = OT = 8 cm
Therefore, AP = OP − AP = 17 cm − 8 cm = 9 cm