ICSE Revision Notes for Constructions Class 10 Maths
Chapter Name | Constructions |
Topics Covered |
|
Related Study |
Construction of Tangent to a Circle at any Point on the Circle
Construction of Tangent to a Circle at any Point on the Circle (with or without using the centre)
A line which touches a circle’s boundary at any point is called a tangent to that circle and the point is called the point of contact.
In the above figure, line l touches the circle at point P, which is the point of contact. Thus, line l is a tangent to the circle. Also, OP is the radius of the circle and OP is perpendicular to l.
Let us learn how to draw a tangent with the help of an example by considering a circle having radius 5.4 cm.
Steps of construction are as follows:
Step 1: Draw a circle with centre O, having radius 5.4 cm.
Now we know what a tangent is and how to draw it using the centre of a circle. Now we will learn how to draw a tangent to a circle without using its centre.
Do you remember the property of angles in alternate segment?
It states that if a line is drawn through an end point of a chord of a given circle in such a way that it the angle it forms with the chord is equal to the angle subtended by the chord in the corresponding alternate segment, then the line is tangent to that circle.
Consider the figure below.
Here, BC is a chord to the circle.
Let us take any point A and draw line segments BA and CA.
Draw a line PQ touching point C. If PQ is a tangent to the circle, then by tangent-secant property, the angle between tangent and secant at point of contact, i.e. ∠BCQ, should be equal to the angle in the corresponding alternate segment, i.e. ∠BAC.
∴ ∠BCQ = ∠BAC
Similarly, if we consider chord AC, then ∠ACP = ∠ABC.
Conversely, if by using chord BC and by taking C as the vertex, we draw ∠BCQ, such that ∠BCQ = ∠BAC, then the line containing CQ will be a tangent to the circle.
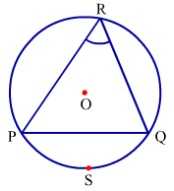
Now, let us draw a tangent through point Q on a circle of radius 4.6 cm.
Step 1: Draw a circle of radius 4.6 cm. Take point Q anywhere on it and draw a chord QP of any length.
Step 2: Take a point R anywhere on the alternate arc of QSP and join R to Q and P.
Step 3: Draw a ray QA such that ∠PQA = ∠PRQ.
Similarly, we can draw a tangent through any point on the circle.
Let us go through some examples to understand the concept better.
Example 1: Draw a tangent to a circle of radius 4.8 cm at a point Q by using the centre of the circle. Also, write the steps of construction.
Answer
The stepwise construction of the tangent to a circle having radius 4.8 cm is as follows:
Step 1: Draw a circle with centre O having radius 4.8 cm.
Step 2: Take a point Q on the circle and draw a ray OQ.
Step 3: Draw a line l perpendicular to OQ at point Q.
Line l is the required tangent.
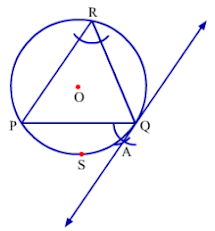
Example 2: Draw a circle of radius 6.2 cm and take a point A on it. Draw a tangent through point A without using the centre.
Answer
The stepwise construction of the tangent through point A on a circle having radius 6.2 cm is as follows:
Step 1: Draw a circle of radius 6.2 cm. Take point A anywhere on it and draw a chord AB of any length.
Step 2: Take a point C anywhere on the alternate arc of ADB and join C to A and B.
Step 3: Draw a ray AP such that ∠BAP = ∠BCA.
Line containing ray AP is the required tangent.
Construction of Tangents to a Circle from a Point outside the Circle
We know that a tangent is perpendicular to the radius through the point of contact. Therefore, if we want to draw a tangent at a point of a circle, we have to simply draw the radius through that point and draw a line perpendicular to that radius. It will be the required tangent at that point.
However, we do not follow this method, when a point lies outside the circle. This is because we do not know at which point on the circle the radius should be drawn so that the line joining that point and the point outside the circle is perpendicular to the radius.
Now, let us solve some examples to understand the construction better.
Example 1: Draw a pair of tangents to a circle of radius 4 cm from a point outside the circle such that the tangents are inclined at an angle of 70°.
Answer
We can draw the tangents using a property of circles. It is given that the tangents are inclined at an angle of 70°. Therefore, the radii joining the points of contacts to the centre of the circle are inclined at an angle of 110° as shown in the figure.
Thus, PT and PQ are the required tangents that are inclined at an angle of 70°.
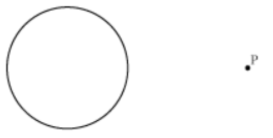
Example 2: Draw a pair of tangents from point P to the given circle.
AnswerIn the given figure, the centre of the circle is not given. Therefore, first of all, we will find the centre of the circle.
For this, let us draw two non-parallel chords of the circle and draw their perpendicular bisectors. The point of intersection of these perpendicular bisectors is the centre O of the circle.
Now, we join the line segment OP and draw its perpendicular bisector. Let this perpendicular bisector intersect OP at point M.
Then we draw a circle with radius equal to OM taking M as centre. Let this circle intersect the given circle at points T and Q. We join PT and PQ.
Thus, PT and PQ are the required tangents from a point P outside the circle.
Construction of Circumcircle of a Triangle
We know that a circle which passes through all the vertices of ΔABC is called circumcircle of ΔABC.
Now, suppose the sides of a ΔABC are given as AB = 5 cm, BC = 5.4 cm, and CA = 6 cm and we are required to construct a circumcircle of ΔABC.
Let us now look at one more example to understand the construction of circumcircle more clearly.
Example: Construct a ΔPQR such that ∠Q = 60°, QR = 4 cm, and QP = 5.7 cm. Also, construct the circumcircle of this triangle.
Answer
The steps of construction are as follows:
- Draw a triangle PQR with ∠Q = 60°, QR = 4 cm, and QP = 5.7 cm
- Draw perpendicular bisector of any two sides, say QR and PR. Let these perpendicular bisectors meet at O.
- With O as centre and radius equal to OP, draw a circle. The circle so drawn passes through the points P, Q, and R, and is the required circumcircle of ΔPQR.
Construction of Incircle of a Triangle
Suppose we have to construct an incircle of a triangle ABC and the following information about the ΔABC is given:
∠B = 60°, ∠C = 60°, and BC = 5.5 cm
Let us now look at one more example to understand this concept better.
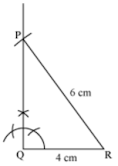
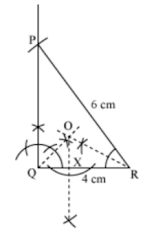
Example: Construct a right triangle ΔPQR, right angled at Q, such that QR = 4 cm and PR = 6 cm. Also construct the incircle of ΔPQR.
Answer
The steps of construction are as follows:
- Draw a ΔPQR right-angled at Q with QR = 4 cm and PR = 6 cm
- Draw bisectors of ∠Q and ∠R. Let these bisectors meet at the point O.
- From O, draw OX perpendicular to the side QR.
- With O as centre and radius equal to OX, draw a circle. The circle so drawn touches all the sides of ΔPQR and is the required incircle of ΔPQR.
Construction of Circumcircle and Incircle of a given Regular Hexagon
We know that circumcircle of a given polygon touches all of its vertices and its incircle touches all of its sides.
Suppose ABCDEF is a regular hexagon of side 5 cm and we have to construct its circumcircle as well as incircle.
How will we construct them?
Let us see.
Let us look at one example in order to understand the above concepts better.
Example 1: Draw circumcircle and incircle of a regular hexagon of side 8.5 cm.
Answer
The steps of construction to construct the circumcircle are as follows:
- Draw a regular hexagon ABCDEF of side 8.5 cm.
- Draw perpendicular bisectors of sides AB and BC. Let them intersect at a point O.
- With O as centre and radius equal to OA, draw a circle.
We observe that the circle touches all the vertices A, B, C, D, E, and F of the regular hexagon ABCDEF. Hence, it is the required circumcircle of the regular hexagon.
The steps of construction to construct the incircle of regular hexagon ABCDEF of side 8.5 cm are as follows:
- Draw a regular hexagon ABCDEF of side 8.5 cm.
- Draw the bisectors of ∠B and ∠C. Let them meet at I.
- From I, draw IN perpendicular to BC.
- Taking I as centre and radius equal to IN, draw a circle.