NCERT Notes for Class 9 Math Chapter 14 Statistics Notes

Class 9 Maths Chapter 14 Statistics Notes

Chapter Name	Statistics Notes
Class	CBSE Class 9
Textbook Name	Statistics Class 9
Related Readings	Notes for Class 9 Notes for Class 9 Maths Revision Notes for Statistics

Statistics

Statistics is the study of collection, organization, analysis and interpretation of data.

Data

A distinct piece of information in the form of fact or figures collected or represented for any specific purpose is called Data. In Latin, it is known as the Datum.

Collection of Data

Data are generally of two types

Primary Data
Secondary Data

Primary Data

Data collected from any firsthand experience for an explicit use or purpose is known as Primary Data

Secondary data

Data collected by any third party for a different purpose other than the user is known as Secondary Data.

Presentation of Data

After collecting data it is important to present it in a meaningful manner. There are many ways to present data.

1. Ungrouped Data

Raw Data- If there is no change in the data and it is in the same form as it is collected then it is said to be raw data.
Example: The marks obtained by 10 students in a Sanskrit test are
55 36 95 73 60 42 25 78 75 62
Range- The difference between the highest and the lowest number of data is called Range.
Frequency Distribution- When the number of items is large then we can convert it into the tabular form which is called a Frequency Distribution Table.
Frequency is the number of times the item comes in the table.

2. Grouped Data

To present the very large number of items in a data we use grouped distribution table.

Class Interval –The group used to classify the data is called the class interval i.e. 20 – 30, 30 – 40.
Upper Limit - In each class interval, the greatest number is the upper-class limit.
Lower Limit – In each class interval, the smallest number is the lower class limit.
Class Size – It is the difference between the upper limit and the lower limit i.e. 10.
Class Mark – The midpoint of each class interval is the class mark.

Grouped data could be of two types as below:

(i) Inclusive or discontinuous Frequency Distribution – If the upper limit of one class is different from the lower limit next class then it is said to be an Inclusive or discontinuous Frequency Distribution.

(ii) Exclusive or continuous Frequency Distribution – If the upper limit of one class is the same as the lower limit of the next class then it is said to be exclusive or continuous Frequency Distribution

Graphical Representation of Data

As you know a picture is better than thousand words so represent data in an easier way is to represent it graphically. Some of the methods of representing the data graphically are

1. Bar Graph

It is the easiest way to represent the data in the form of rectangular bars so it is called Bar graph.

The thickness of each bar should be the same.
The space between in bar should also be same.
The height of the bar should be according to the numerical data to be represented.

Example: Represent the average monthly rainfall of Nepal for the first six months in the year 2014.

Month	Jan	Feb	Mar	Apr	May	Jun
Average rainfall	45	65	40	60	75	30

Solution

On the x-axis mark the name of the months.
On the y-axis mark the class interval which we have chosen.
Then mark the average rainfall respective to the name of the month by the vertical bars.
The bars could be of any width but should be same.
This is the required bar graph.

2. Histogram

It is like the Bar graph only but it is used in case of a continuous class interval.

The class intervals are to be taken along an x-axis.
The height represents the frequencies of the respective class intervals.

Example: Draw the histogram of the following frequency distribution.

Daily earnings (in Rs)	700 – 750	750 – 800	800 – 850	850 – 900	900 – 950	950 – 1000
No. of stores	6	9	2	7	11	5

Solution

Mark the daily earnings on the x-axis.
Mark the no. of stores on the y-axis.
As the scale is starting from 700 so we will mark the zigzag to show the break.
Mark the daily earnings through the vertical bars.

3. Frequency Polygon

To draw the frequency polygon

First, we need to draw a histogram
Then join the midpoint of the top of the bars a line segment and the figure so obtained is required frequency polygon.
The midpoint of the first bar is to be joined with the midpoint of the imaginary interval of the x-axis
The midpoint of the last bar is to be joined with the midpoint of the next interval of the x-axis.

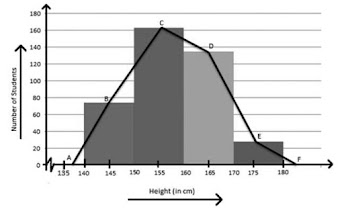
If we need to draw the frequency polygon without drawing the histogram then first we need to calculate the class mark of each interval and these points will make the frequency polygon.

Example: Draw the frequency polygon of a city in which the following weekly observations were made in a study on the cost of living index without histogram.

Classes	Class – marks	Frequency
140 – 150	145	5
150 – 160	155	10
160 – 170	165	20
170 – 180	175	9
180 – 190	185	6
190 – 200	195	2
Total		52

Step 1: First of all we need to calculate the class mark of each class interval.

Step 2: Take the suitable scale and represent the class marks on the x-axis.

Step 3: Take the suitable scale and represent the frequency distribution on the y-axis.

Step 4: To complete the frequency polygon we will join it with the x-axis before the first class and after the last interval.

Step 5: Now plot the respective points and join to make the frequency polygon.

Measures of Central Tendency

To make all the study of data useful, we need to use measures of central tendencies. Some of the tendencies are

1. Mean

The mean is the average of the number of observations. It is calculated by dividing the sum of the values of the observations by the total number of observations.

It is represented by x bar or.

The meanof n values x₁ , x₂ , x₃ , ...... x_n is given by

Mean of Grouped Data (Without Class Interval)

If the data is organized in such a way that the frequency is given but there is no class interval then we can calculate the mean by

where, x₁ , x₂ , x₃ , ...... x_n are the observations

f₁ , f₂ , f₃ , ...... f_n are the respective frequencies of the given observations.

Example

Grouped Population Mean
x	f	fx
20	40	800
40	60	2400
60	30	1800
80	50	4000
100	20	2000
	200	Σfx = 11000

Here, x₁ , x₂ , x₃ , x₄ , and x₅ are 20, 40, 60, 80, 100 respectively. and f₁ , f₂ , f₃ , f₄ , f₅ are 40 , 60 , 30 , 50 , 20 respectively.

2. Median

The median is the middle value of the given number of the observation which divides into exactly two parts.

For median of ungrouped data, we arrange it in ascending order and then calculated as follows

Median (Average)

Let we consider an ungroup/raw data as follow:

Your FIRST step is to arrange them in ascending order like

Then check what is the middle value of the data

If the number of the observations is odd then the median will be . As in the above figure the no. of observations is 7 i.e. odd, so the median will be term.
= 4th term.
The fourth term is 44.
If the number of observations is even then the median is the average of n/2 and (n/2) +1 term.

Example: Find the median of the following data.

6, 7, 10, 12, 13, 4, 8, 12

(i) First, we need to arrange it in ascending order.

4, 6, 7, 8, 10, 12, 12, 13

(ii) The no. of observation is 8. As the no. of observation is even the median is the average of n/2 and (n/2)+1.

(iii)
(iv) 4th term is 8 and the 5th term is 10.
(v) So the median Image

3. Mode

The mode is the value of the observation which shows the number that occurs frequently in data i.e. the number of observations which has the maximum frequency is known as the Mode.

Example: Find the Mode of the following data:

15, 20, 22, 25, 30, 20,15, 20,12, 20

Solution

Here, the number 20 appears the maximum number of times so

Mode = 20.

Remark: The empirical relation between the three measures of central tendency is

3 Median = Mode + 2 Mean