NCERT Notes for Class 9 Maths Chapter 12 Constructions

Class 9 Maths Chapter 12 Constructions Notes
Chapter Name | Constructions Notes |
Class | CBSE Class 9 |
Textbook Name | Constructions Class 9 |
Related Readings |
|
Constructions
Constructions tell us about the steps of drawing of perfect geometrical figures like triangle, circle, polygons etc. by using geometrical tools with the given measurements.
Geometry Box
To draw the geometrical figures we need some geometrical instruments which we can find in the geometry box. Some instruments are:
Graduated scaleThis is the scale to make the straight lines. Its one side is marked with centimetres and millimetres and the other side is marked with inches.

A pair of set squares
It is a set of two squares. One with 90°, 60° and 30° angles and other with angles 90°, 45° and 45°.

Divider
It helps in measuring the length.

Compass
It is used to draw the circles and angles.

Protector
It is used to mark and measure the angles.

Geometrical Construction
In the Geometrical construction, we use only two instruments: (i) A non graduated ruler also called a Straight Edge and (ii) a compass for drawing a geometrical figure. For measurements, we may use a graduated scale and protractor also.
Basic Constructions
Construction 1: How to construct the bisector of an angle?
If we have to bisect the ∠BOA, then we need to follow these steps to construct the bisector of the angle.
Step 1: Take O as the centre and draw an arc by any radius intersecting the rays OA and OB at X and Y respectively.
Step 2: Now take X and Y as the centre and Draw arcs which intersects each other at a point C with radius more than (1/2) XY.
In the above example, ∠BOA = 80° and OC bisects it in ∠BOC and ∠COA which is 40° each.

Construction 2: How to construct the perpendicular bisector of a given line segment?
We have to bisect the given line segment AB.
Step 1: Take A and B as the centres and radius more than 1/2 of Ab and draw the arcs on both sides.
Step 3: Here CD intersects AB at point M so that M is the midpoint of AB and CMD is the required perpendicular bisector of AB.

Join A and B to both C and D to form AC, AD, BC and BD.
In triangles CAD and CBD,
AC = BC (Arcs of equal radii)
AD = BD (Arcs of equal radii)
CD = CD (Common)
Therefore, ∆ CAD ≅ ∆CBD (SSS rule)
So, ∠ ACM = ∠ BCM (CPCT)
Now in triangles CMA and CMB,
AC = BC (As before)
CM = CM (Common)
∠ ACM = ∠ BCM (Proved above)
Therefore, ∆ CMA ≅ ∆ CMB (SAS rule)
So, AM = BM and ∠ CMA = ∠ CMB (CPCT)
As ∠ CMA + ∠ CMB = 180° (Linear pair axiom),
Now we get
∠ CMA = ∠CMB = 90°.
Therefore, CMD is the perpendicular bisector of AB.
Construction 3: How to construct an angle of 60° at the initial point of a given ray?
We have to draw an angle of 60° at the given point P.
Step 1: Take P as the centre and draw an arc of any radius which intersects PQ at point B.
Step 2: Now Take B as a centre and draw an arc with the same radius as before which intersects the previous arc at point A.
Step 3: Now draw a ray PR which passé through Point A and the ∠RPQ is the required angle of 60°.
Join AB.
Then, AP = AB = PB (By construction)

Therefore, ∆ ABP is an equilateral triangle and the ∠ APB, which is the same as ∠ RPQ is equal to 60°.
Construction of Triangles
By using the properties of the triangle and the above basic constructions we can construct triangles.
Construction 1: How to construct a triangle if its base, a base angle and sum of other two sides are given?
Given the base BC, a base angle ∠B and the sum of other two sides AB + AC of a triangle ABC, now we need to construct it.
Steps of Construction:
Step 1: First of all, draw the base BC and at the point B make an ∠XBC equal to the given angle.
Step 2: From the ray BX, cut the line segment BD = AB + AC.
Step 3: Join DC now which make ∠DCY = ∠BDC.
Step 4: When CY intersect BX at A then it form the required triangle i.e. ABC.

Construction 2: How to construct a triangle if its base, a base angle and the difference of the other two sides are given?
Given the base BC, a base angle i.e. ∠B and the difference of the other two sides AB – AC or AC – AB, we need to construct the triangle ABC. There could be two cases:
Case (i): If AB > AC that is AB – AC is given.
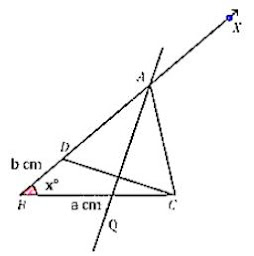
Step 1: Draw the base BC which is equal to a cm and at point B make an ∠XBC = x°.
Step 2: From ray, BX cut the line segment BD which is equal to AB – AC.
Step 3: Join DC and draw the perpendicular bisector of DC.
Step 4: This perpendicular bisector intersects BX at a point A. By joining A to C we get the required triangle i.e. ∆ABC.
Case (ii): If AB < AC that is AC – AB is given.
Steps of Construction:

Step 1: Draw the base BC and at point B make an ∠XBC.
Step 2: From ray, BX cut the line segment BD which is equal to AC – AB from the line BX by extending it on opposite side of line segment BC.
Step 3: Join DC and draw the perpendicular bisector of DC.
Step 4: Let PQ intersect BX at A and by joining A to C, we get the required triangle ∆ABC.
Construction 3: How to construct a triangle if its perimeter and two base angles are given?
Given the base angles, say ∠ B and ∠ C and BC + CA + AB, you have to construct the triangle ABC.
Steps of Construction:
Step 1: Draw a line segment XY = BC + CA + AB.
Step 2: Make ∠LXY = ∠B and ∠MYX = ∠C.
Step 3: Now bisect ∠ LXY and ∠ MYX. These bisectors will intersect at a point A.
Step 4: Draw perpendicular bisectors PQ of AX and RS of AY.
Step 5: Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC.
Then, ABC is the required triangle.

