NCERT Exemplar Solutions for Class 10 Maths Chapter 11 Area Related to Circles Exercise 11.4

Chapter 11 Area Related to Circles NCERT Exemplar Solutions Exercise 11.4 Class 10 Maths

Chapter Name	NCERT Maths Exemplar Solutions for Chapter 11 Area Related to Circles Exercise 11.4
Book Name	NCERT Exemplar for Class 10 Maths
Other Exercises	Exercise 11.1 Exercise 11.2 Exercise 11.3
Related Study	NCERT Solutions for Class 10 Maths

Exercise 11.4 Solutions

Long Answer Questions

1. The area of a circular playground is 22176 m² . Find the cost of fencing this ground at the rate of Rs 50 per metre. 

Solution
Area of the circular playground = 22176 m² 
Let r be the radius of the circle. 
πr² = 22176 
⇒ (22/7)r² = 22176 
⇒ r² = 22176 × (22/7)
⇒ r² = 7056 
⇒ r = 84 
Radius of the circular playground = 84 m
Circumference of the circle = 2πr 
= 2 × (22/7) × 84 
= 528 m 
Cost of fencing 1 meter of ground = Rs. 50 
Cost of fencing the total ground = Rs. 528 × 50
= Rs. 26,400

2. The diameters of front and rear wheels of a tractor are 80 cm and 2 m respectively. Find the number of revolutions that rear wheel will make in covering a distance in which the front wheel makes 1400 revolutions.

Solution

Diameter of front wheels = d₁  = 80 cm 
Diameter of rear wheels = d₂ = 2 m = 200 cm 
Let r₁ be the radius of the front wheels = 80/2 = 40 cm 
Let r₂ be the radius of the rear wheels = 200/2 = 100 cm 
Circumference of the front wheels = 2πr 
= 2 × (22/7) × 40
= 1760/7   cm 
Circumference of the rear wheels = 2πr 
= 2 × (22/7) × 100 
= 4400/7 cm 
No. of revolutions made by the front wheel = 1400 
∴ Distance covered by the front wheel  = 1400 × (1760/7) 
= 352000 cm 
Number of revolutions made by rear wheel in covering a distance in which the front wheel makes 1400 revolutions, 
= (Distance covered by front wheel)/(Circumference of rear wheel)
= 352000/4400/7
= (352000 × 7)/4400
= 560 revolutions.

3. Sides of a triangular field are  15m, 16m and 17m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals. 

Solution

Sides of the triangle are 15m, 16m, and 17m. 
Now, 
Perimeter of the triangle  = (15 + 16 + 17)m 
= 48 m 
Semi - perimeter of the triangle = s 
= 48/2
= 24 m 
By Heron's formula, 
Area of the triangle = 

Let B, C and H be the corners of the triangle on which buffalo, cow and horse are tied respectively with ropes of 7 m each.

So, the area grazed by each animal will be in the form of a sector.
Radius of each sector = r
= 7 m
Let x, y, z be the angles at corners B, C, H respectively.

Area of field not grazed by the animals = Area of triangle – (area of the three sectors)
= 109.892 – 77
= 32.982 cm² 

4. Find the area of the segment of a circle of radius 12 cm whose Corresponding sector has a central angle of 60° (Use π = 3.14). 

Solution

Radius of the circle = r 
= 12 cm 
OA = OB = 12 cm
∠ AOB = 60°  (given)

As triangle OAB is an isosceles triangle,
∠ OAB = ∠ OBA = θ   (let)
And, Sum of interior angles of a triangle is 180°,
θ + θ + 60° = 180°
⇒ 2θ = 120°
⇒ θ = 60°
Therefore, the triangle AOB is an equilateral triangle.
AB = OA = OB = 12 cm
Area of the triangle AOB = (√3/4) × a², 
where a is the side of the triangle. 
= (√3/4) × (12)² 
= (√3/4) × 144
= 36√3 cm² 
= 62.354 cm² 
Also, Central angle of the sector AOBCA = ∅ 
= 60°
= 60π/180  
= π/3    radians 
So, area of the sector AOBCA = (1/2)r² ∅
= (1/2) × 12² × π/3
= 75.36 cm² 
Area of the segment ABCA  = Area of the sector AOBCA - Area of the triangle AOB 
= (75.36 - 62.354)cm² 
= 13.006 cm² 

5. A circular pond is 17.5 m is of diameter. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of Rs. 25 per m² .

Solution

Diameter of the circular pond = 17.5 m
Let r be the radius of the park = r 
r = 8.75 m 

The circular pond is surrounded by a path of width 2 m.
Radius of the outer circle = R
= (8.75+2) m
= 10.75 m
Area of the road = Area of the outer circular path – Area of the circular pond
πr² - πR² 
= 3.14 × (10.75)² - 3.14 × (8.75)² 
= 3.14 × (10.75)² - (8.75)² 
= 3.14 × (10.75 + 8.75) × 10.75 - 8.75)
= 3.14 × 19.5 × 2 
= 122. 46 m² 
So, the area of the path is 122.46 m² .
Now, Cost of constructing the path per m² = Rs. 25 
Cost of constructing 122.46 m² of the path  = Rs. 25 × 122.46 
= Rs. 3061.50

6. In Fig., ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centers A, B, C and D have been drawn, then find the area of the shaded region of the figure.

Solution

AB = 18 cm,
DC = 32 cm
Distance between AB and DC = Height = 14 cm
Now,
Area of the trapezium = (1/2) × (Sum of parallel sides) × Height
= (1⁄2) × (18+32) × 14
= 350 cm² 
We have,
AB ∥ DC,
∠ A +∠ D = 180°
∠ B +∠ C = 180°
Radius of each arc = 7 cm
Area of sector with ∠A = (∠A/180) × πr² 
Area of sector with ∠B = (∠B/360) × πr² 
Area of sector with ∠C = (∠C/360) × πr² 
Area of sector with ∠D = (∠D/360) × πr² 
Therefore, 
Sum of total areas of sectors = 

Area of shaded region = Area of trapezium - (Total area of sectors)
= 350 - 154 
= 196 cm² 
Therefore, the required area of shaded region is 196 cm².

7. Three circles each of radius 3.5 cm are draw in such a way that each of them touches the other two. Find the area enclosed between these circles. 

Solution

The three circles are drawn such that each of them touches the other two.

By joining the centers of the three circles,
AB = BC = CA = 2(radius)
= 7 cm
So, triangle ABC is an equilateral triangle with each side 7 cm.
Area of the triangle = (√3/4) × a² , Where a is the side of the triangle. 
= (√3/4) × 7² 
= (49√3/4)  cm² 
= 21.2176 cm² 
Central angle of each sector = 60°
= (60π/180)
= π/3 radians 
Area of each sector = (1/2)r² θ
= (1/2) × (3.5)² × (π/3) 
= 12.25 × [22/(7×6)]
= 6.4167 cm² 
Total area of three sectors = 3 × 6.4167
= 19.25 cm² 
Area enclosed between three circles = Area of triangle ABC - Area of the three sectors 
= 21.2176 - 19.25
= 1.9676 cm² 
Therefore, the required are enclosed between these circles is 1.967 cm² (approx).

8. Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm. 

Solution

Radius of the circle  = r = 5 cm 
Arc length of the sector = l = 3.5 cm 
Let the central angle (in radians ) be θ. 

We have,
Arc length = Radius × Central angle (in radians)
Central angle (θ) = Arc length / Radius
= l/r
= 3.5/5
= 0.7 radians
Area of the sector = (1⁄2) × r²θ
= (1⁄2) × 25 × 0.7
= 8.75 cm² 
Therefore, required area of the sector of a circle is 8.75 cm².

9. Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.

Solution

The four circles are placed such that each piece touches the other two pieces.

By joining the centers of the circles by a line segment, we get a square ABDC with sides,
AB = BD = DC = CA = 2(Radius)
= 2(7) cm
= 14 cm
Area of the square = (Side)² 
= (14)² 
= 196 cm² 
ABDC is a square,
So, each angle has a measure of 90°.
∠ A = ∠ B = ∠ D = ∠ C = 90° = π/2 radians
= θ   (let)
Radius of each sector = 7 cm
Area of the sector with central angle A = 1⁄2 r²θ
= 1⁄2 × 49 × π/2
= 1⁄2 × 49 × (22/(2×7))
= (77/2) cm² 
As the central angles and the radius of each sector are same, area of each sector is 77/2 cm² 
Area of the shaded portion = Area of square – Area of the four sectors
= 196 – (4 × (77/2))
= 196 – 154
= 42 cm²
Therefore, required area of the portion enclosed between these pieces is 42 cm².

10. On a square cardboard sheet of area 784 cm² , four congruent circular plates of maximum size are placed such that each circular plate touches the other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.

Solution

Area of the square = 784 cm² 
Side of the square = √Area
= √784
= 28 cm
The four circular plates are congruent,
Then diameter of each circular plate = 28/2
= 14 cm
Radius of each circular plate = 7 cm
We know that,
Area of the sheet not covered by plates = Area of the square – Area of the four circular plates
As all four circular plates are congruent,
We have,
Area of all four plates equal.
Area of one circular plate = πr² .
= (22/7)× 7² 
= 154 cm² 

Area of four plates = 4 × 154 
= 616 cm² 
Area of the sheet not covered by plates = 784 - 616 
= 168 cm² 

11. Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in Fig. Find the area of floor that remains uncovered with tiles. (Use π = 3.14). 

Solution

Length = 5 m 
Breadth  = 4m
Area = l × b
= 20 m² 
Diameter of each circular tile = 50 cm 
Radius = 25 cm 
= 1/4 m 
Now, 
Area of circular tile ; 
= πr² 
= 3.14 × (1/4)² 
= 3.14/6 
Area of 80 circular tiles  = 80 × (3.14/16) = 1.57 m² 
Area which remain uncovered Area of floor - Area of 80 circular tiles 
= 20 - 15.7 
= 4.3 m² 

12. All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if area of the circle is 1256 cm² . (Use π = 3.14). 

Solution

Let the radius of the circle be r. 

Area of circle = 1256 cm² 
πr² = 1256 
⇒ r = 20 cm 
So, Diameter = 40 cm
As, all the vertices of a rhombus lie on a circle that means each diagonal of a rhombus must pass through the center of a circle that is why both diagonals are equal and same as the diameter of the given circle.
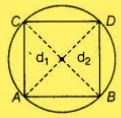
Let d₁ and d₂ be the  diagonals of rhombus, 
And, Diameter of circle = 40 cm
Area of rhombus = (1/2) × d₁ × d₂ 
= (1/2) × 40 × 40 
= 800 cm² 

13. An archery target has three regions formed by three concentric circles as shown in Fig.. If the diameters of the concentric circles are in the ratio 1: 2:3, then find the ratio of the areas of three regions.

Solution

Let the diameters of concentric circles be k, 2k and 3k. 

Radius of concentric circle are  = k/2, k, 3k/2 

Required ratio = A₁ : A₂ : A₃ 
= 1 : 3 : 5 

14. The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 a m and 6 : 40 a m.

Solution

We know that in 60 minute hand revolve = 360°
In 1 min = 360/60 In (6 : 05 am to 6 :40 am ) = 35 minutes, 

= 360/60 × 35 
= 210 
Length of minute hand (r) = 5 cm 
Area of sector AOBA with angle O = (πr² /360) × ∠O

 (π5² /360) × 210 
= 275/6 
= 45(5/6) cm² 

15. Area of a sector of central angle 200° of  a circle is 770 cm² . Find the length of the corresponding arc of this sector. 

Solution

Let the radius of the sector AOBA be r.

Central Angle =200°

Area of sector =770 cm² 

Area of sector = (πr² /360) × θ
⇒ 770 = (πr² /360) × 200
⇒ r = 21 cm 
Length of corresponding arc of this sector = Central angle × Radius 
= 200 × 21 × π/180
= 220/3 
= 77(1/3) cm 

16. The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?

Solution

Let the lengths of the corresponding arc be l₁ and l₂ .

Radius of the sector PO₁QP=7cm

Radius of the sector AO₂BA=21cm

And,

Central angle of sector PO₁QP=120°

Central angle of sector AO₂BA=40°

Hence, we observe that arc lengths of two sectors of two different circles may be equal but their area need not be equal. 

17. Find the area of the shaded region given in Fig.

Solution

Construction : 

Join JK, KL, LM and MJ, 
There are four equally semi - circles and LMJK formed a square. 

FH = 14 - (3 + 3) 
= 8 cm 

Side of square = 4 cm 

Radius of semicircle = 2 cm 

Now,

Area of square JKLM = 4² = 16 cm² 
Area of semicircle HJM = πr²/2
= π2²/2 = 2π 
= 6.28 cm² 
Area of four semicircle = 4 × 6.28 
= 25.12 cm² 
Now, 
Area of square ABCD = 14² 
= 196 cm² 
Area of shaded region = area of square ABCD - (Area of  4 semicircle + area of square JKLM) 
= 196 - (8π + 16)
= 180 - 8π  cm² 

18. Find the number of revolutions made by a circular wheel of area 1.54 m² in rolling a distance of 176 m. 

Solution

Let us take the number of revolutions made by a circular wheel be n and the radius of circular wheel be r. 

Area of circular wheel = 1.54 m² 

πr² = 1.54 
⇒ (22/7)r² = 1.54 
⇒ r = 0.7 m 
Distance travelled by circular wheel in one revolution = Circumference of circular wheel 
= 2πr 
= 2 × (22/7)× 0.7 
= 4.4 m 

Distance travelled by circular wheel = 176 m 
Number of revolutions  = (Total distance)/(Distance of revolution) 
= 176/4.4
= 40 

19. Find the difference of the areas of two segment of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.

Solution

Let the radius of the circle be r. 

OA = OB = r cm 

We have, 

AB = 5 cm 

Central angle of AOBA = 90°
In Δ AOB, AB² = OA² + OB² 
5² = r² + r² 
⇒ r = 5/√2 cm 

Also, AD = DB = 5/2 cm 

Now, In ΔADO, 
OA² = OD² + AD² 
= [5/√2)² - [5/2]² 
= 5/2 cm 

Area of isosceles ΔAOB = (1/2) × base × height 

= (1/2) × 5× 52
= 25/4 cm² 

Area of sector AOBA = (πr² /360) × θ

Area of minor segment = Area of sector AOBA - Area of isosceles ΔAOB 
= [25π/8 - 25/4]
Now, Area o circle = πr² 
= π(5/√2)² 
= 25π/2
Area of major segment = Area of circle  - Area of minor segment 

= (25π/2) - [25π/8 - 25/4]
= (75π/8 + 25/4)
Now, Difference  = Area of major segment - Area of minor segment 
= (75π/8 + 25/4) - (25π/8 - 254)
= 25π/4 + 25/4  cm² 

20. Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.

Solution

Radius of the circle (r) = 21 cm and 

Central angle of the sector AOBA(θ) = 120°

Area of circle = πr² 
= (22/7) × (21)² 
= 1386 cm² 

Area of minor sector (OABA) = (πr² /360) × θ
= (22/7) × [(21)²/360] × 120°
= 462 cm² 

Area of major sector = Area of circle  - Area of min or sector 

= 1386 - 432 
= 924 cm² 

Difference of area of major and min or sector, 
= 924 - 462
= 462 cm²