Chapter 10 Congruent Triangles RD Sharma Solutions Exercise 10.4 Class 9 Maths

Chapter Name	RD Sharma Chapter 10 Congruent Triangles Exercise 10.4
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 10.1 Exercise 10.2 Exercise 10.3 Exercise 10.5 Exercise 10.6
Related Study	NCERT Solutions for Class 10 Maths

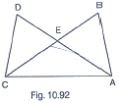
1. In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.

Solution

Given that in the figure AB = CD and AD = BC.

We have to prove

ΔADC ≅ ΔCBA
Now,

Consider ΔADC and ΔCBA,

We have

AB = CD [Given]
BC = AD [Given]
And AC = AC [Common side]

So, by SSS congruence criterion, we have

ΔADC ≅ ΔCBA

∴ Hence proved

2. In a ΔPQR, if PQ = QR and L, M and N are the mid - points of the sides PQ, QR and RP respectively. Prove that LN = MN.

Solution

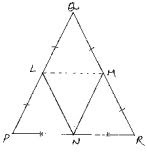
Given that in ΔPQR, PQ = QR and L, M and N are mid - points of PQ, QR and RP respectively

We have to prove LN = MN.

Join L and M, M and N, N and L

We have

PL = LQ, QM = MR and RN = NP

[∵ L, M and N are mid - points of PQ, QR and RP respectively]

And also,

PQ = QR ⇒ PL = LQ = QM = MR = PQ/2 = QR/2 ...(1)

Using mid - point theorem, we have

MN || PQ and MN = (1/2)(PQ)

⇒ [MN = PL = LQ] ...(2)

Similarly, we have

LN || QR and LN = (1/2)(QR)

⇒ LN = QM = MR

From equation (1), (2) and (3), we have

PL = LQ = QM = MR = MN = LN

∴ LN = MN

RD Sharma Solutions for Class 9 Chapter 10 Congruent Triangles Exercise 10.4