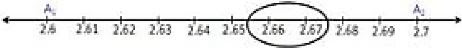RD Sharma Solutions for Class 9 Chapter 1 Number System Exercise 1.6

Chapter 1 Number System RD Sharma Solutions Exercise 1.6 Class 9 Maths

Chapter Name	RD Sharma Chapter 1 Number System Exercise 1.6
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 1.1 Exercise 1.2 Exercise 1.3 Exercise 1.4 Exercise 1.5
Related Study	NCERT Solutions for Class 10 Maths

Exercise 1.6 Solutions

Mark the correct alternative in each of the following : 

1. Which one of the following is a correct statement?
(a) Decimal expansion of a rational number is terminating 
(b) Decimal expansion of a rational number is non - terminating 
(c) Decimal expansion of an irrational number is terminating 
(d) Decimal expansion of an irrational number is non - terminating and non - repeating 

Solution 

The following steps for successive magnification to visualise 2.665 are : 
(a) We observe that 2.665 is located somewhere between 2 and 3 on the number line. So, let us look at the portion of the number line between 2 and 3. 

(b) We divide this portion into 10 equal parts and mark each point of division. The first mark to the right of 2 will represent 2.1, the next 2.2 and soon. Again we observe that 2.665 lies between 2.6 and 2.7 . 

(c) We mark these points A₁ and A₂ respectively. The first mark on the right side of A₁ , will represent 2.61, the number 2.62, and soon. We observe 2.665 lies between 2.66 and 2.67 . 

(d) Let us mark 2.66 as B₁ and 267 as B₂ .Again divide the B₁ B₂ into ten equal parts. The first mark on the right side of B₁ will represent 2.661 . Then next 2.662, and so on. 
Clearly, fifth point will represent 2.665.

2. Which one of the following statements is true ? 

(a) The sum of two irrational numbers is always an irrational number 
(b) The sum of two irrational numbers is always a rational number. 
(c) The sum of two irrational numbers may be a rational number or an irrational number 
(d) The sum of two irrational numbers is always an integer 

Solution

Once again we proceed by successive magnification, and successively decrease the lengths of the portions of the number line in which 5.37 is located. First, we see that  5.37 is located between 5 and 6. In the next step, we locate  5.37 between 5.3 and 5.4. To get a more accurate visualization of the representation, we divide this portion of the number line into lo equal parts and use a magnifying glass to visualize that 5.37 lies between 5.37 and 5.38. To visualize 5.37 more accurately, we again divide the portion between 5.37 and 5.38 into ten equal parts and use a magnifying glass to visualize that S.S lies between 5.377 and 5.378. Now to visualize 5.37 still more accurately, we divide the portion between 5.377 and 5.378 into 10 equal parts, and visualize the representation of 5.37 as in fig.,(iv) . Notice that 5.37 is located closer to 5.3778 than to 5.3777(iv)