RD Sharma Solutions for Class 9 Chapter 1 Number System Exercise 1.5

Chapter 1 Number System RD Sharma Solutions Exercise 1.5 Class 9 Maths

Chapter Name	RD Sharma Chapter 1 Number System Exercise 1.5
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 1.1 Exercise 1.2 Exercise 1.3 Exercise 1.4 Exercise 1.6
Related Study	NCERT Solutions for Class 10 Maths

Exercise 1.5 Solutions

1. Complete the following sentences : 
(i) Every point on the number line corresponds to a ― number which many be either ― or ―.
(ii) The decimal form of an irrational number is neither ― nor ― 
(iii) The decimal representation of a rational number is either ― or ―
(iv) Every real number is either ― number or ― number . 

Solution

(i) Every point on the number line corresponds to a Real number which may be either rational or irrational. 
(ii) The decimal form of an irrational number is neither terminating nor repeating . 
(iii) The decimal representation of a rational number is either terminating, non - terminating or recurring.
(iv)  Every real number is either a rational number or an irrational number.

2. Represent √6 , √7, √8 on the number line. 

Solution

Draw a number line and mark point O, representing zero, on it

Suppose point A represents 2 as shown in the figure 
Then OA = 2. 
Now, draw a right triangle OAB such that AB = 1. 
By Pythagoras theorem, we have
OB² = OA² + AB² 
⇒ OB² = 2² + 1² 
⇒ OB² = 4 + 1 = 5
⇒ OB = √5
Now, draw a circle with center O and radius OB.
We fine that the circle cuts the number line at A
Clearly, OA₁ = OB = radius of circle = √5
Thus, A₁ represents √5 on the number line,
But, we have seen that √5 is not a rational number. Thus we find that there is a point on the number
which is not a rational number.
Now, draw a right triangle OA₁B₁ , Such that A₁B₁ = AB = 1
Again, by Pythagoras theorem, we have
(OB₁)² = (OA₁)² + (A₁B₁)²
⇒ (OB₁)² = (√5)² + (1)²
⇒ (OB₁)² = 5 + 1 = 6
⇒ OB₁ = √6
Draw a circle with center O and radius OB₁ = √6 . This circle cuts the number line at A₂ as shown in figure.
Clearly OA₂ = OB₁ = √6
Thus, A₂ represents √6 on the number line.
Also, we know that √6 is not a rational number.
Thus, A₂ is a point on the number line not representing a rational number .
Continuing in this manne, we can represent √7 and √8 also on the number lines as shown in the figure
Thus, OA₃ = OB₂ = √7 and OA₄ = OB₃ = √8

3. Represent √3.5, √9.4, √10.5 on the real number line.

Solution

Given to represent √3.5, √9.4, √10.5 on the real number line
Representation of √3.5 on real number line: 
Steps involved : 
(i) Draw a line and mark A on it.  

(ii) Mark a point B on the line drawn in step - (i) such that AB = 3.5 units 

(iii) Mark a point C on AB produced such that BC = 1unit 

(iv) Find mid - point of AC. Let the midpoint be O 
⇒ AC = AB + BC = 3.5 + 1 =  4.5 
⇒ AO = OC = AC/2 = 4.5/2 = 2.25 

(v) Taking O as the center and OC = OA as radius drawn a semi - circle. Also draw a line passing through B perpendicular to OB. Suppose it cuts the semi - circle at D.
Consider triangle OBD, it is right angled at B. 
BD² = OD² - OB² 
⇒ BD² = OC² - (OC - BC)²  [∵ OC = OD = radius]
⇒ BD² = 2OC. BC - (BC)² 
⇒ BD = √[2 ×2.25×1-(1)² ]
⇒ BD = √35 

(vi) Taking B as the center and BD as radius draw an arc cutting OC produced at E. point 
E so obtained represents √3.5 as BD = BE = √3.5 = radius 
Thus, E represents the required point on the real number line. 

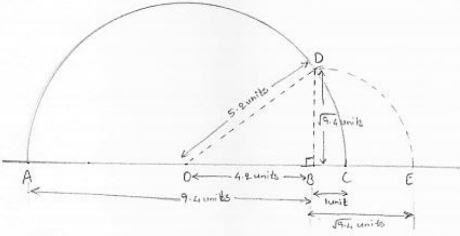
Representation of  √9.4 on real number line steps involved : 
(i) Draw and line and mark A on it 

(ii) Mark a point B on the line drawn in step (i) such that AB = 9.4 units 
(iii) Mark a point C on AB produced such that BC = 1 unit. 
(iv) Find midpoint of AC. Let the midpoint be O. 
⇒ AC = AB + BC = 9.4 + 1 = 10.4 units 
⇒ AD = OC = AC/2 = 10.4/2 = 5.2 units 
(v) Taking O as the center and OC = OA as radius draw a semi - circle. Also draw a line passing through B perpendicular to OB. Suppose it cuts the semi - circle at D. 
Consider triangle OBD, it is right angled at B> 
⇒ BD² = OD² - OB² 
⇒ BD² =  OC² - (OC - BC)²   [∵ OC = OD = radius] 
⇒ BD² = OC² - (OC² - 2OC. BC + (BC)² )
⇒ BD² = 2OC. (BC - (BC² ))
⇒ BD² = √[2×(5.2)1-1²]
⇒ BD = √9.4 units 
(vi) Taking B as center and BD as radius draw an arc cutting OC produced at E so obtained represents √9.4 as BD = BE = √9.4 = radius 
Thus, E represents the required point on the real number line. 

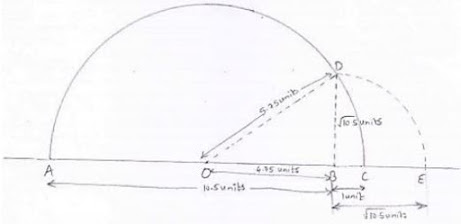
Representation of √10.5 on the real number line:
Steps involved: 
(i) Draw a line and mark A on it 

(ii) Mark a point B on the line drawn in step (i) such that AB = 10.5 units 
(iii) Mark a point C on AB produced such that BC = 1 unit 
(iv) Find midpoint of AC. Let the midpoint be O. 
⇒ AC = AB + BC = 10.5  +1 = 11.5 units 
⇒ AO  = OC = AC/2 = 11.5/2 = 5.75 units 
(v) Taking O as the center and OC = OA as radius, draw a semi - circle. Also draw a line passing through B perpendicular to DB. Suppose it cuts the semi - circle at D. Consider triangle OBD, it is right angled at B 

(vi) Taking B as the center and BD as radius draw on arc cutting OC produced at E. Point E so obtained represents √10.5 as BD = BE = √10.5 radius arc 
Thus, E represents the required point on the real number line

4. Find whether the following statements are true or false. 
(i) Every real number is either rational or irrational. 
(ii) It is an irrational number. 
(iii) Irrational numbers cannot be represented by points on the number line 

Solution

(i) True
As we know that rational and irrational numbers taken together from the set of real numbers.
(ii) True
As, π is ratio of the circumference of a circle to its diameter, it is an irrational number
⇒ π = 2πr/2r
(iii) False
Irrational numbers can be represented by points on the number line.