Chapter 14 Co-Ordinate Geometry RD Sharma Solutions Exercise 14.3 Class 10 Maths
Chapter Name | RD Sharma Chapter 14 Co-Ordinate Geometry |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 14.3 Solutions
1. Find the coordinates of the point which divides the line segment joining (-1, 3) and (4, -7) internally in the ratio 3 : 4.
Solution
Let P(x, y) be the required point. 
2. Find the points of trisection of the line segment joining the points:
(i) (5, -6) and (-7, 5),
(ii) (3, -2) and (-3, -4)
(iii) (2, -2) and (-7, 4).
Solution
(i) Let P and Q be the point of trisection of AB i.e., AP = PQ = QB 
3. Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1) , (1, 0), (4, 3) and (1, 2) meet.
Solution
4. Prove that the points (3, -2), (4, 0), (6, -3) and (5, -5) are the vertices of a parallelogram.
Solution
Here mid - point of AC - Mid - point of BD i.e., diagonals AC and BD bisect each other.
We know that diagonals of a parallelogram bisect each other
∴ABCD is a parallelogram.
5. Three consecutive vertices of a parallelogram are (-2, -1), (1, 0) and (4, 3). Find the
fourth vertex.
Solution
6. The points (3, -4) and (-6, 2) are the extremities of a diagonal of a parallelogram. If the
third vertex is (-1, -3). Find the coordinates of the fourth vertex.
Solution
7. Find the ratio in which the point (2, y) divides the line segment joining the points A (-2,
2) and B ( 3, 7). Also, find the value of y.
Solution
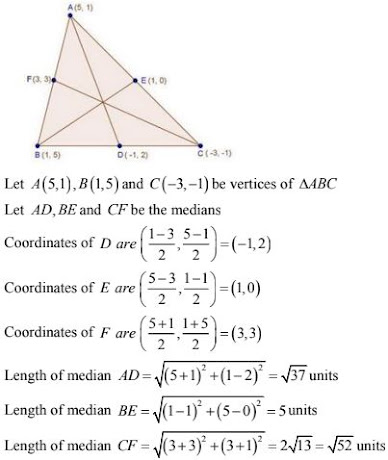
8. If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, find the length of
the median through A.
Solution
find the vertices of the triangle.
Solution
10. If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2, 3)
and (5, 2), find the other vertices.
Solution
11. (i) (i) In what ratio is the line segment joining the points (-2, -3) and (3, 7) divided by the y-
axis? Also, find the coordinates of the point of division.
(ii) In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point
(-5, -21/5) ?
Solution
value of k.
Solution
13. Determine the ratio in which the straight line x - y - 2 = 0 divides the line segment
joining (3, -1) and (8, 9).
Solution
14. 14. Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by
(i) x-axis
(ii) y-axis.
Also, find the coordinates of the point of division in each case.
Solution
15. Prove that the points (4, 5), (7, 6), (6, 3), (3, 2) are the vertices of a parallelogram. Is it a
rectangle.
Solution
Solution
17. Prove that the points (-4, -1), (-2, -4), (4, 0) and (2, 3) are the vertices of a rectangle.
Solution
18. Find the lengths of the medians of a triangle whose vertices are A (−1, 3), B (1, −1) and C
(5,1).
Solution
the fourth vertex.
Solution
20. If two vertices of a parallelogram are (3, 2), (-1, 0) and the diagonals cut at (2, -5), find
the other vertices of the parallelogram.
Solution
21. If the coordinates of the mid-points of the sides of a triangle are (3, 4), (4, 6) and (5, 7),
find its vertices.
Solution
B such that A is nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value
of k.
Solution
23. If the points (—2 , —1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x
and y.
Solution
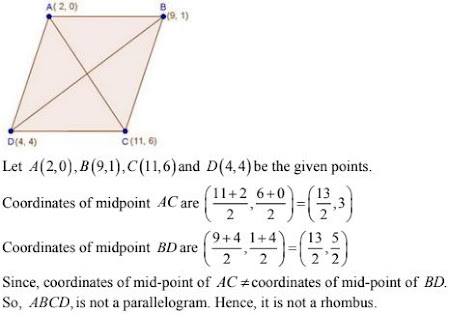
24. The points A (2, 0), B (9, 1), C (11, 6) and D (4, 4) are the vertices of a quadrilateral
ABCD. Determine whether ABCD is a rhombus or not.
Solution
25. If three consecutive vertices of a parallelogram are (1, —2), (3, 6) and (5, 10), find its
fourth vertex.
Solution
26. If the points A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram
ABCD, find the values of a and b.
Solution
27. If the coordinates of the mid-points of the sides of a triangle be (3, -2), (-3, 1) and (4, -3), then find the coordinates of its vertices.
Solution
28. Find the lengths of the medians of a ΔABC having vertices at A (0, -1), B (2, 1) and C (0,
3).
Solution
29. Find the lengths of the medians of a ΔABC having vertices at A (5, 1), B (1, 5), and C
(−3,-1).
Solution
30. Find the coordinates of the points which divide the line segment joining the points (−4, 0)
and (0, 6) in four equal parts.
Solution
31. Show. that the mid - point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
Solution
Let A(5, 7), B(3, 9), C(8, 6) and D(0, 10) be the given points
32. Find the distance of the point (1, 2) from the mid - point of the line segment joining the points (6, 8) and (2, 4).
Solution
33. If A and B are (1, 4) and (5, 2) respectively, find the coordinates of P when AP/BP = 3/4
Solution
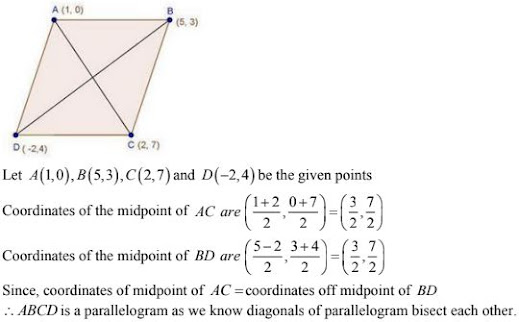
34. Show that the points A (1, 0), B ( 5, 3), C ( 2, 7) and D (-2, 4) are the vertices of a
parallelogram.
Solution
35. Determine the ratio in which the point P (m, 6) divides the join of A(-4, 3) and B(2, 8).
Also, find the value of m.
Solution
Also find the value of a.
Solution
37. The line segment joining the points(3, -4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (P, -2) and (5/3, Q) respectively. Find the values of P and Q.
Solution
38. The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0. Find the value of k.
Solution
39. If A and B are two points having coordinates (-2, -2) and (2, -4) respectively, find the
coordinates of P such that AP = AB.
Solution
40. Find the coordinates of the points which divide the line segment joining A (—2, 2) and B
(2, 8) into four equal parts.
Solution
41. A (4, 2), B (6, 5) and C (1, 4) are the vertices of ΔABC.
(i) The median from A meets BC in D. Find the coordinates of the point D.
(ii) Find the coordinates of point P on AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of the points Q and R on medians BE and CF respectively such
that BQ : QE = 2 : l and CR : RF 2 : 1.
(iv) What do you observe?
Solution
42. ABCD is a rectangle formed by joining the points A (-1, -1), B (-1, 4), C (5, 4) and D
(5, −1). P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively. Is the
quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Solution
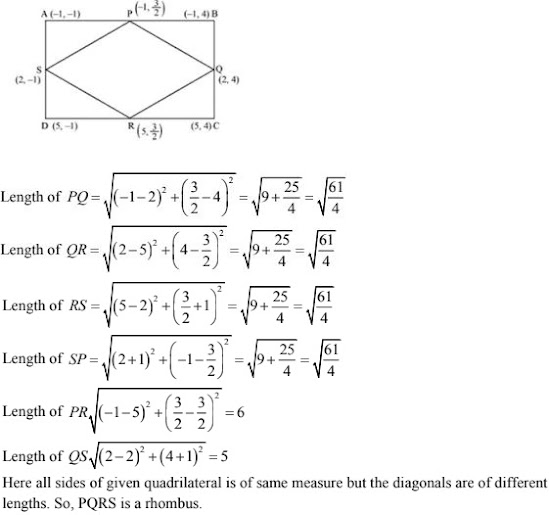
43. Show that A(-3, 2), B(-5, -5), C(2, -3) and D(4, 4) are the vertices of a rhombus.
Solution
Hence, ABCD is a rhombus.
44. Find the ratio in which the y-axis divides the line segment joining the points (5, -6) and (-1, - 4). Also, find the coordinates of the point of division.
Solution
Let P(5, -6) and Q(-1, -4) be the given points. Let y - axis divide PQ in the ratio k : 1
Then, the coordinates of the point of division are
45. If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram
taken in order, then find the values of k and p.
Solution
Let A(6, 1), B(8, 2), C(9, 4) and D(k, p) be the given points.
Since ABCD is a parallelogram
Coordinates of midpoint of AC = Coordinates of the midpoints of BD
Solution
Let (-4, 6)
Divide AB internally in the ratio k : 1 using the section formula, we get
Divide AB internally in the ratio k : 1 using the section formula, we get
You c check for the y - coordinate also. So, the point (-4, 6) divides the line segment j joining the points A(-6, 10) and B(3, -8) in the ratio 2 : 7
47. Find the coordinates of a point A, where AB is a diameter of the circle whose centre is (2,
-3) and B is (1, 4).
Solution
Let coordinates of point A be (x, y)
Mid - point of diameter AB is center of circle (2, -3)
Mid - point of diameter AB is center of circle (2, -3)
48. A point P divides the line segment joining the points A (3, -5) and B (-4, 8) such that AP/PB = k/1. If P lies on the line x + y = 0, then find the value of y.
Solution
Given points are A(3, -5) and B(-4, 8)P divides AB in the ratio k : 1,
Using the section formula, we have :
Coordinate of point P are [{(-4k + 3)/(k + 1)(8k - 5)/(k + 1)}]
Now it is given, that P lies on the line x + y = 0
Therefore
Now it is given, that P lies on the line x + y = 0
Therefore
