RD Sharma Solutions for Class 10 Chapter 14 Co-Ordinate Geometry Exercise 14.2

Chapter 14 Co-Ordinate Geometry RD Sharma Solutions Exercise 14.2 Class 10 Maths

Chapter Name	RD Sharma Chapter 14 Co-Ordinate Geometry
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 14.1 Exercise 14.3 Exercise 14.4 Exercise 14.5
Related Study	NCERT Solutions for Class 10 Maths

Exercise 14.2 Solutions

1. Find the distance between the following pair of points:
(i) (-6, 7) and (-1, -5)
(ii) (a + b, b + c) and (a - b, c -b)
(iii) (a sin α, -b cos α)  and (-a cos α, b sin α)
(iv) (a, 0) and (0, b) 

Solution

2.  Find the value of a when the distance between the points (3, a) and (4, 1) is √10.

Solution

3. If the points (2, 1) and (1, -2) are equidistant from the point (x, y) from (-3, 0) as well as from (3, 0) are 4. 

Solution

We have P(2, 1) and Q(1, -2) and R(X, Y) 
Also, PR = QR 

4. Find the values of x, y if the distances of the point (x, y)  from (-3, 0) as well as from (3, 0) are 4. 

Solution

5. The length of a line segment is of 10 units and the coordinates of one end - point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end. 

Solution

Let two ordinate of the other end R be Y 

∴ Coordinates of other end R are (10, y) i.e., R(10, y) 
Distance PR = 10  [given]

6. Show that the points (-2, -4), (4, 0) and (2, 3) are the vertices points of are the vertices points of a rectangle. 

Solution

7. Show that the points A(1, -2), B(3, 6), C(5, 10) and D(3, 2)  are the vertices of a parallelogram 

Solution

8. Prove that the points A(1, 7), B(4, 2), C(-1, -1)  and D(-4, 4) are the vertices of a square. 

Solution

Let A(1, 7), B(4, 2), C(-1, -1) and D(-4, 4) be the given point. One way of showing that ABCD is a square is to use the property that all its sides should be equal and both its diagonals should also be equal 

Now, 

Since, AB = BC = CD = DA and AC= BD, all the four sides of the quadrilateral ABCD are equal and its diagonals AC and BD are also equal. Therefore, ABCD is a square. 

9. Prove that the points (3, 0) (6, 4) and (-1,3) are vertices of a right angled isosceles triangle. 

Solution

Let A(3,0), B(6, 4) and C(-1, 3) be the given points 

 

10. Prove that (2, - 2), (-2, 1)  and (5, 2) are the vertices of a right angled triangle. Find the area of the triangle and the length of the hypotenuse.  

Solution

Let A(2, -2), B(-2, 1) and C(5, 2) be the given points  

11. Prove that the points (2a, 4a) , (2a, 6a) arid (2a + √3a, 5a) be the vertices of an equilateral triangle. 

Solution

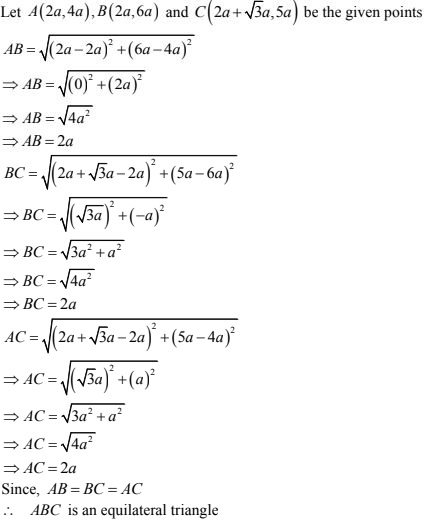
12. Prove that the points (2, 3), (-4, -6) and (1,3/2) do not form a triangle. 

Solution

Let A(2, 3), B(-4, -6) and C(1, 3/2) be the given points 

We know that for a triangle sum of two sides is greater than the third side. Here AC + BC is not greater than AB. 

∴ ABC is not triangle 

13. An equilateral triangle has two vertices are (2, -1), (3, 4), (-2, 3) and (-3, -2) find the coordinates of the third vertex. 

Solution

Let A(3, 4), B(-2, 3) and C(x, y) be the three vertices of the equilateral triangle then, 

14. Show that the quadrilateral whose vertices are (2, -1) (3, 4), (-2, 3) and (-3, -2) is a rhombus. 

Solution

Let A(2, -1), B(3, 4), C(-2, 3) and D(-3, -2) 

15. Two vertices of an isosceles triangle are (2, 0) and (2, 5). Find the third vertex if the length of the equal side is 3. 

Solution

Two vertices of an isosceles triangle are A(2, 0) and B(2, 5). Let C(x, y) be the third vertex 

16. Which point on x-axis is equidistant from (5, 9) and (-4, 6)? 

Solution

Let A(5, 9) and B(-4, 6) be the given points. 

Let C(x, 0) be the point on x - axis 

Now, 

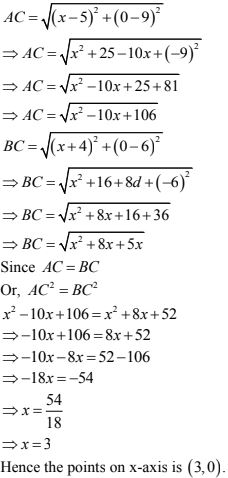
17. Prove that the points(-2, 5), (0, 1) and (2, -3) are collinear. 

Solution

Let A (-2,5), B(0, 1) and C(2, - 3) be the given points 

18. The coordinates of the point P are (-3, 2). Find the coordinates of the point Q which lies on the line joining P and origin such that OP = OQ. 

Solution

Let the coordinates of Q be (x,y) 
Since Q lies on the line joining P and O (origin) and OP = OQ
By mid - point theorem 

(x -3)/2 = 0 and (y + 2)/2 = 0 
∴ x = 3, y = -2 
Hence coordinates of points Q are (3, -2) 

19. Which point on y - axis is equidistant from (2, 3) and (-4, 1) ?

Solution

A(2, 3) and B(-4, 1) are the given points. 

Let C(0, y) be the points are y - axis 

20. The three vertices of a parallelogram are (3, 4), (3, 8) and (9, 8).  Find the fourth vertex. 

Solution

Let A(3, 4), B(3, 8) and C(9, 8) be the given points 

Let the forth vertex be D(x, y) 

21. Find the circumcenter of the triangle whose vertices are (-2, -3), (-1, 0), (7, -6). 

Solution

Circumcenter of a triangle is the point of intersection of all the three perpendicular bisectors of the sides of triangle. So, the vertices of the triangle lie on the circumference of the circle. 

Let the coordinates of the circumcenter of the triangle be (x, y) 

∴ (x, y)  will the equidistant from the vertices of the triangle. 

22. Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0). 

Solution

Let the point P(0, 100) and Q(10, 0) be the given points. 

∴ The angle subtended by the line segment PQ at the origin O is 90° . 

23. Find the centre of the circle passing through(5, -8), (2, -9) and (2, 1). 

Solution

Let the center of the circle be O (x, y) 
Since radii of the circle is constant 

Hence, distance of O from A(5, -8), B(2, -9) and C(2, 1) will be constant and equal 

24. Find the value of k, if the point P(0, 2) is equidistant from (3, k) and (k, 5).

Solution

Let the point P(0, 2) is equidistant from A(3, k) and (k, 5)
PA = PB 

25. If two opposite vertices of a square are (5, 4) and (1, -6), find the coordinates of its remaining two vertices.

Solution

Let ABCD be a square and let A(5, 4)  and C(1, -6) be the given points. 

Let (x, y)  be the coordinates of B. 

AB = BC

26. Show that the points(-3, 2), (-5, -5), (2, -3) and (4, 4) are the vertices of a rhombus. 
Find the area of this rhombus. 

Solution

27. Find the coordinates of the circumcenter of the triangle whose vertices are (3, 0), (-1, -6) and (4, -1). Also, find its circumradius. 

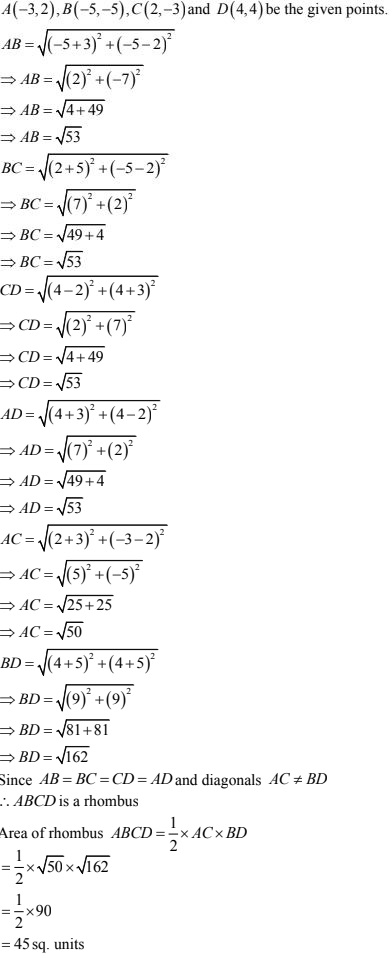
Solution

Let A(3, 0), B(-1, -6) and C(4, -1) be the given points. 
Let O(x, y) be the circumcenter of the triangle

OA = OB = OC 

28. Find a point on the x - axis which is equidistant from the points (7, 6) and (-3, 4). 

Solution

Let A(7, 6) and B(-3, 4) be the given points. 
Let P(x, 0) be the point on x - axis such that PA = PB
PA = PB 

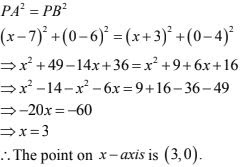
29. (i) Show that the points A(5, 6), B(1, 5) C(2, 1) and D(6, 2) are the vertices of a square. 

(ii) Prove that the points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1) are the vertices of a square ABCD. 

Solution

A(5, 6), B(1, 5), C(2, 1) and D(6, 2) are the given points 

30. Find the point on x-axis which is equidistant from the points (-2, 5) and (2, -3). 

Solution

31. Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6,—1), (1,

3) and (x, 8) respectively.

Solution

P(6, -1), Q(1, 3) and R(x, 8) are the given points. 

PQ = QR 

32. Prove that the points (0, 0), (5, 5) and (-5, 5) are the vertices of a right isosceles triangle .

Solution

Let A(0, 0), B(5, 5) and C(-5, 5) be the given points 

33. If the point P(x, y ) is equidistant from the points A(5, 1) and B (1, 5), prove that x = y.

Solution

Since P(x, y) is equidistant from A(5, 1) and B(1, 5) 
AP = BP 

34. If Q (0, 1) is equidistant from P (5, —3) and R (x, 6), find the values of x. Also, find the

distances QR and PR

Solution

35. Find the values of y for which the distance between the points P (2, —3) and Q (10, y) is

10 units

Solution

Given that distance between (2, -3) and (10, y) is 10 

36. Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3) 

Solution

37. Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two vertices. 

Solution

38. Name the quadrilateral formed, if any, by the following points, and give reasons for your answers: 

(i) A(-1, -2), B(1, 0), C(-1, 2), D(-3, 0)
(ii) A(-3, 5), B(3, 1), C(0, 3), D(-1, -4) 
(iii) A(4, 5), B(7, 6), C(4, 3), D(1, 2) 

Solution

39. Find the equation of the perpendicular bisector of the line segment joining points (7, 1) and (3, 5). 

Solution

Bisector passes through midpoint 

40. Prove that the points (3, 0), (4, 5), (—1, 4) and (—2, —1), taken in order, form a rhombus.

Also, find its area.

Solution

41. In the seating arrangement of desks in a classroom three students Rohini, Sandhya and Bina are seated at A (3, 1), B (6, 4) and C (8, 6). Do you think they are seated in a line?

Solution

Let A(3, 1), B(6, 4) and C(8, 6) be thee given points 

Since, AB + BC = AC
Points A, B, C are collinear 

Hence, Rohini, Sandhya and Bina are seated in a line 

42. Find a point on y - axis which is equidistant from the points (5, -2) and (-3, 2). 

Solution 

Let A(5, -2) and B(-3, 2) be the given points, 

Let P(0, y) be the point on y - axis 

PA = PB 

43. Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4). 

Solution

44. If a point A(0, 2) is equidistant from the point B(3, p) and C(p, 5), then find the value of p.

Solution

A(0, 2), B(3, P) and C(p, 5) are given points 

It is given that AB = AC