Chapter 17 Perimeter and Area of Plane Figures RS Aggarwal Solutions Exercise 17B Class 10 Maths

Chapter Name | RS Aggarwal Chapter 17 Perimeter and Area of Plane Figures |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Perimeter and Area of Plane Figures Exercise 17B Solutions
1. The perimeter of a rectangular plot of land is 80 cm and its breadth is 16 m. Find the length and area of the plot.
Solution
As, a perimeter = 80 m
⇒ 2(length + breadth) = 80
⇒ 2(length + 16) = 80
⇒ 2 × length + 32 = 80
⇒ 2 × length = 80 – 32
⇒ length = 48/2
∴ length = 24 m
Now, the area of the plot = length × breadth
= 24 × 16
= 384 m2
So, the length of the plot is 24 m and its area is 384 m2.
2. The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
Solution
Let the breadth of the rectangular park be h.
∴ Length of the rectangular park = l = 2b
Perimeter = 840 m
⇒ 840 = 2(l + b)
⇒ 840 = 2(2b + b)
⇒ 840 = 2(3b)
⇒ 840 = 6b
⇒ b = 140 m
Thus, we have:
l = 2b
= 2 × 140
= 280 m
Area = l × b
= 280 × 140
= 39200 m2
3. One side of a rectangular is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
Solution
One side of the rectangle = 12 cm
Diagonal of the rectangle = 37 cm
The diagonal of a rectangle forms the hypotenuse of a right-angled triangle. The other two sides of the triangle are the length and the breadth of the rectangle.
Now, using Pythagoras’ theorem, we have:
(one side)2 + (other side)2 = (hypotenuse)2
⇒ (12)2 + (other side)2 = (37)2
⇒ 144 + (other side)2 = 1369
⇒ (other side)2 = 1329 – 144
⇒ (other side)2 = 1225
⇒ Other side = 35 cm
Thus, we have:
Length = 35 cm
Breadth = 12 cm
Area of the rectangle = 35 × 12 = 420 cm2
4. The area of a rectangular plot is 426 m2 and is length is 28 m. Find its perimeter.
Solution
Area of the rectangular plot = 462 m2
Length (l) = 28 m
Area of a rectangle = Length (l) × Breadth(b)
⇒ 462 = 28 × b
⇒ b = 16.5 m
Perimeter of the plot = 2(l + b)
= 2(28 + 16.5)
= 2 × 44.5
= 89 m
5. A lawn is in the form of a rectangle whose sides are in the ratio 5 : 3. The area of the lawn is 3375 m2. Find the cost of fencing the lawn at ₹ 65 per metre.
Solution
Let the length and breadth of the rectangular lawn be 5x m and 3x m, respectively.
Given:
Area of the rectangular lawn = 3375 m2
⇒ 3375 = 5x × 3x
⇒ 3375 = 15x2
⇒ 3375/15 = x2
⇒ 225 = x2
⇒ x = 15
Thus, we have:
l = 5x = 5 × 15 = 75 m
b = 3x = 3 × 15 = 45 m
Perimeter of the rectangular lawn = 2(l + b)
= 2(75 + 45)
= 2(120)
= 240 m
Cost of fencing 1 m lawn = Rs 65
∴ Cost of fencing 240 m lawn = 240 × 65
= Rs 15, 600
6. A room is 16 m long and 13.5 m broad. Find the cost of covering its floor with 75-m-wide carpet at ₹ 60 per metre.
Solution
As, the area of the floor = length × breadth
= 16 × 13.5
= 216 m2
And, the width of the carpet = 75 m
So, the length of the carpet required = (Area of the floor)/(Width of the carpet)
= 216/75
= 2.88 m
Now, the cost of the carpet required = 2.88 × 60 = 172.80
Hence, the cost of covering the floor with carpet is 172.80
Disclaimer, The answer given in the textbook is incorrect. The same has been rectified above.
7. The floor of a rectangular hall is 24 m long and 18 m wide. How many carpets, each of length 2.5 m and breadth 80 cm, will be required to cover the floor of the hall ?
Solution
Given:
Length = 24 m
Breadth = 18 m
Thus, we have:
Area of the rectangular hall = 24 × 18
= 432 m2
Length of each carpet = 2.5 m
Breadth of each carpet = 80 cm = 0.80 m
Area of one carpet = 2.5 × 0.8 = 2 m2
Number of carpets required = (Area of the hall)/(Area of the carpet) = 432/2 = 126
Therefore, 216 carpets will be required to cover the floor of the ball.
8. A 36-m-long, 15 m broad verandah is to be paved with stones, each measuring 6 dm by 5 dm. How many stones will be required ?
Solution
Area of the verandah = Length × Breadth
= 36 × 15
= 540 m2
Length of the stone = 6dm = 0.6 m
Breadth of the stone = 5 dm = 0.5 m
Area of one stone = 0.6 × 0.5 = 0.3 m2
Number of stones required = (Area of the verendah)/(Area of the stone)
= 540/(0.3)
= 1800
Thus, 1800 stones will be required to pave the verandah.
9. The area of rectangle is 192 cm2 and its perimeter is 56 cm. Find the dimensions of the rectangle.
Solution
Area of the rectangle = 192 cm2
Perimeter of the rectangle = 56 cm
Perimeter = 2(length + breadth)
⇒ 56 = 2(l + b)
⇒ l + b = 28
⇒ l = 28 – b
Area = length × breadth
⇒ 192 = (28 – b) x b
⇒ 192 = 28b – b2
⇒ b2 – 28b + 192 = 0
⇒ (b – 16)(b – 12) = 0
⇒ b = 16 or 12
Thus, we have;
l = 28 – 12
⇒ l = 28 – 12
⇒ l = 16
We will take length as 16 cm and breadth as 12 cm because length is greater than breadth by convention.
10. A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
Solution
The field is planted with grass, with 2.5 m uncovered on its sides.
The field is shown in the given figure.

Thus, we have;
Length of the area planted with grass 35 – (2.5 + 2.5) = 35 – 5 = 30 m
Width of the area planted with grass = 18 – (2.5 + 2.5) = 18 – 5 = 13 m
Area of the rectangular region planted with grass = 30 × 13 = 390 m2
11. A rectangular plot measure 125 m by 78 m. It has travel path 3 m wide all around on the outside. Find the area of the path and the cost of travelling it at ₹ 75 per m2.
Solution
The plot with the travel path is shown in the figure.

Area of the rectangular plot = l × b
Area of the rectangular plot = 125 × 78 = 9750 m2
Length of the park including the path = 125 + 6 = 131 m
Breadth of the park including the path = 78 + 6 = 84 m
Area of the plot including the path = 131 × 84
= 11004 m2
Area of the path = 11004 – 9750
= 1254 m2
Cost of travelling 1 m2 of the path = Rs 75
Cost of travelling 1254 m2 of the path = 1254 × 75
= Rs 94050
12. A footpath of uniform width runs all around the inside of a rectangular field 54 m long and 35 m wide. If the area of the path is 420 m2, find the width of the path.
Solution
Area of the rectangular field = 54 × 35 = 1890 m2
Let the width of the path be x m. The path is shown in the following diagram:

Length of the park excluding the path = (54 – 2x) m
Breadth of the park excluding the path = (35 – 2x) m
Thus, we have:
Area of the path = 420 m2
⇒ 420 = 54 × 35 – (54 – 2x)(35 – 2x)
⇒ 420 = 1890 – (1890 – 70x - 108x + 4x2)
⇒ 420 = - 4x2 + 178x
⇒ 4x2 – 178x + 420 = 0
⇒ 2x2 – 89x + 210 = 0
⇒ 2x2 – 84x – 5x + 210 = 0
⇒ 2x(x – 42) – 5(x – 42) = 0
⇒ (x – 42)(2x – 5) = 0
⇒ x – 42 = 0 or 2x – 5 = 0
⇒ x = 42 or x = 2.5
The width of the path cannot be more than the breadth of the rectangular field.
∴ x = 2.5 m
Thus, the path is 2.5 m wide.
13. The length and breadth of a rectangular garden are in the ratio 9 : 5. A path 3.5 m wide, running all around inside it has an area of 1911 m2. Find the dimensions of the garden.
Solution
Let the length and breadth of the garden be 9x and 5x m, respectively,
Now,
Area of the garden = (9x × 5x) = 45x2
Length of the garden excluding the path = (9x – 7)
Breadth of the garden excluding the path = (5x – 7)
Area of the path = 45x2 = [(9x – 7)(5x – 7)]
⇒ 1911 = 45x2 – [45x2 – 63x – 35x + 49]
⇒ 1911 = 45x2 – 45x2 + 63x + 35x – 49
⇒ 1911 = 98x – 49
⇒ 1960 = 98x
⇒ x = 1960/98
⇒ x = 20
Thus, we have:
Length = 9x = 20 × 9 = 180 m
Breadth = 5x = 5 × 20 = 100 m
14. A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
Solution
Width of the room left uncovered = 0.25 m
Now,
Length of the room to be carpeted = 4.9 – (-0.25 + 0.25) = 4.9 – 0.5 = 4.4 m
Breadth of the room be carpeted = 3.5 – (0.25 + 0.25) = 3.5 – 0.5 = 3 m
Area to be carpeted = 4.3 × 3 = 13.2 m2
Breadth of the carpeted 80 cm = 0.8 cm
We know:
Area of the room = Area of the carpet
Length of the carpet = (Area of the room)/(Breadth of the carpet)
= 13.5/0.8
= 16.5 m
Cost of 1 m carpet = Rs 80
Cost of 16.5 m carpet = 80 × 16.5 = Rs 1,320
15. A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is 12 m2. Find its width.
Solution
Let the width of the border be x m.
The length and breadth of the carpet are 8 m and 5 m, respectively.
Area of the carpet = 8 × 5 = 40 m2
Length of the carpet without border = (8 – 2x)
Breadth of carpet without border = (5 – 2x)
Area of the border = 12 m2
Area of the carpet without border = (8 – 2x) (5 – 2x)
Thus, we have:
12 = 40 – [(8 – 2x)(5 – 2x)]
⇒ 12 = 40 – (40 – 26x + 4x2)
⇒ 12 = 26x – 4x2
⇒ 26x – 4x2 = 12
⇒ 4x2 – 26x + 12 = 0
⇒ 2x2 – 13x + 6 = 0
⇒ (2x – 1)(x – 6) = 0
⇒ 2x – 1 = 0 and x – 6 = 0
⇒ x = 1/2 and x = 6
Because the border cannot be wider than the entire carpet, the width of the carpet is 1/2 m, i.e., 50 cm.
16. A 80 cm by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of travelling the reads at ₹ 40 per m2.
Solution
The length and breadth of the lawn are 80 m and 64 m, respectively.
The layout of the roads is shown in the figure below:

Area of the road ABCD = 80 × 5 = 400 m2
Area of the road PQRS = 64 × 5 = 320 m2
Clearly, the area EFGH is common in both the roads
Area EFGH = 5 × 5 = 25 m2
Area of the roads = 400 + 320 – 25
= 695 m2
Given:
Cost of travelling 1 m2 area = Rs 40
Cost of travelling 695 m2 area = 695 × 40
= Rs 27,800
17. The dimensions of a room are 14 m × 10 m × 6.5 m. There are two doors and 4 windows in the room. Each door measures 2.5 m × 1.2 m and each window measures 1.5 m × 1 m. Find the cost of painting the four walls of the room at ₹ 35 per m2.
Solution
The room has four walls to be painted
Area of these walls = 2(l × h) + 2(b × h)
= (2×14×6.5) + (2×10×6.5)
= 312 m2
Now, Area of the two doors = (2×2.5×1.2) = 6 m2
Area of the four windows = (4×1.5×1) = 6 m2
The walls have to be painted; the doors and windows are not to be painted.
∴ Total area to be painted = 312 – (6 + 6) = 300 m2
Cost for painting 1 m2 = Rs 35
Cost for painting 300 m2 = 300 × 35 = Rs 10, 500
18. The cost of painting the four walls of a room 12 m long at ₹ 30 per m2 is ₹ 7560 per m2 and cost of covering the floor with the mat at ₹ 25 per m2 is ₹ 2700. Find the dimensions of the room.
Solution
As, the rate of covering the floor = ₹ 25 per m2
And, the cost of covering the floor = ₹ 2700
So, the area of the floor = 2700/25
⇒ length × breadth = 108
⇒ 12 × breadth = 108
⇒ breadth = 108/12
∴ breadth = 9 m
Also,
As, the rate of painting the four walls = ₹ 30 per m2
And, the cost of painting the four walls = ₹ 7560
So, the area of the four walls = 7560/30
⇒ 2(length + breadth) height = 252
⇒ 2(12 + 9) height = 252
⇒ 2(21) height = 252
⇒ 42 × height = 252
⇒ height = 252/42
∴ height = 6 m
So, the dimensions of the room are 12 m × 9 m × 6 m.
19. Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
Solution
Area of the square = 1/2 × Diagonal2
= 1/2 × 24 × 24
= 288 m2
Now, let the side of the square be x m.
Thus, we have:
Area = Side2
⇒ 288 = x2
⇒ x = 12√2
⇒ x = 16.92
Perimeter = 4 × side
= 4 × 16.92
= 67.68 m
Thus, the perimeter of the square plot is 67.68 m.
20. Find the length of the diagonal of a square whose area is 128 cm2. Also, find its perimeter.
Solution
Area of the square = 128 cm2
Area = ½.d2 (where d is a diagonal of the square)
⇒ 128 = ½.d2
⇒ d2 = 256
⇒ d = 16 cm
Now,
Area = Side2
⇒ 128 = Side2
⇒ Side = 11.31 cm
Perimeter = 4(side)
= 4(11.31)
= 45.24 cm
21. The area of a square field is 8 hectares. How long would a man take to cross it diagonally by walking at the rate of 4 km per hour ?
Solution
Given, area of square filed = 8 hectares
= 8 × 0.01 [1 hectare = 0.01 km2]
= 0.08 km2
Now, area of square field = (side of square)2 = 0.08
Distance covered by man along the diagonal of square field = length of diagonal
√2 side = √2 × √2/5 = 2/5 km
Speed of walking = 4 km/h
∴ Time taken = distance/speed = 2/(5 × 4)
= 2/20
= 1/10
= 0.1 hour
= 1/10 × 60 min
= 6 minutes
22. The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
Solution
As, the rate of the harvesting = ₹ 900 per hectare
And, the cost of harvesting = ₹ 8100
So, the area of the square field = 8100/900 = 9 hectare
⇒ the area = 90000 m2 (As, 1 hectare = 10000 m2)
⇒ (side)2 = 90000

So, the cost of putting the fence = 1200 × 18
= ₹ 21,600
23. The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 per 100 m2.
Solution
Cost of fencing the lawn Rs 28000
Let l be the length of each side of the lawn. Then, the perimeter is 4l.
We know:
Cost = Rate × Perimeter
⇒ 28000 = 14 × 41
⇒ 28000 = 56l
Or,
l = 28000/56
= 500 m
Area of the square lawn = 500 × 500
= 250000 m2
Cost of moving 100 m2 of the lawn = Rs 54
Cost of moving 1 m2 of the lawn = Rs 54/100
∴ Cost of moving 250000 m2 of the lawn = (250000 × 54)/100
= Rs 135000
24. In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9 cm and CM = 12 cm. Calculate the area of the quadrilateral.


BD = 24 cm, AL = 9 cm, CM = 12 cm, AL ⊥ BD and CM ⊥ BD
Area of the quadrilateral = ar(∆ABD) + ar(∆BCD)
= 1/2 × BD × AL + 1/2 × BD × CM
= 1/2 × 24 × 9 + 1/2 × 24 × 12
= 108 + 144
= 252 cm2
So, the area of the quadrilateral ABCD is 252 cm2.
25. Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and∆BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
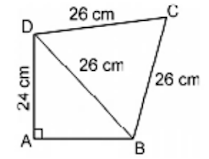
Solution
∆BDC is an equilateral triangle with side a = 26 cm.
Area of ∆BDC = √3/4.a2
= √3/4 × 262
= (1.73)/4 × 676
= 292.37 cm2
By using Pythagoras theorem in the right-angled triangle ∆DAB, we get:
AD2 + AB2 = BD2
⇒ 242 + AB2 = 262
⇒ AB2 = 262 – 242
⇒ AB2 = 676 – 576
⇒ AB2 = 100
⇒ AB = 10 cm
Area of ∆ABD = 1/2 × b × h
= 1/2 × 10 × 24
= 120 cm2
Area of the quadrilateral = Area of ∆BCD + Area of ∆ABD
= 292.37 + 120
= 412.37 cm2
Perimeter of the quadrilateral = AB + AC + CD + AD
= 24 + 10 + 26 + 26
= 86 cm.
26. Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB = 90° and AC = 15 cm.
Solution
In the right angled ∆ACB:
AB2 = BC2 + AC2
⇒ 172 = BC2 + 152
⇒ 172 – 152 = BC2
⇒ 64 = BC2
⇒ BC = 8 cm
Perimeter = AB + BC + CD + AD
= 17 + 8 + 12 + 9
= 46 cm
Area of ∆ABC = 1/2(b × h)
= 1/2(8 × 15)
= 60 cm2
In ∆ADC:
AC2 = AD2 + CD2
So, ∆ADC is a right-angled triangle at D.
Area of ∆ADC = 1/2 × b × h
= 1/2 × 9 × 12
= 54 cm2
∴ Area of the quadrilateral = Area of ∆ABC + Area of ∆ADC
= 60 + 54
= 114 cm2
27. Find the area of the quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and the diagonal BD = 20 cm.


= 336 + 210
= 546 cm2
28. Find the area of a parallelogram with base equal to 25 and the corresponding height measuring 16.8 cm.
Solution
Given:
Base = 25 cm
Height = 16.8 cm
∴ Area of the parallelogram = Base × Height = 25 cm × 16.8 cm = 420 cm2
29. The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm. find the distance between the shorter sides.
Solution
Longer side = 32 cm
Shorter side = 24 cm
Let the distance between the shorter side be x cm.
Area of a parallelogram = Longer side × Distance between the longer sides
= Shorter side × Distance between the shorter sides
or, 32 × 17.4 = 24 × x
or, x = (32 × 17.4)/24 = 23.2 cm
∴ Distance between the shorter sides = 23.2 cm
30. The area of a parallelogram is 392 m2. If its altitude is twice the corresponding base, determined the base and the altitude.
Solution
Area of the parallelogram = 392 m2
Let the base of parallelogram be b m.
Given:
Height of the parallelogram is twice the base
∴ Height = 2b m
Area of a parallelogram = Base × Height
⇒ 392 = b × 2b
⇒ 392 = 2b2
⇒ 392/2 = b2
⇒ 196 = b2
⇒ b = 14
∴ Base = 14 m
Altitude = 2 × Base = 2 × 14
= 28 m
31. The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.

Parallelogram ABCD is made up of congruent ∆ABC and ∆ADC

Now,
Area of the parallelogram = 2 × Area of ∆ABC
= 2 × 336
= 672 cm2
32. Find the area of the rhombus, the length of whose diagonals are 30 cm and 16 cm. Also, find the perimeter of the rhombus.
Solution
Area of the rhombus = 1/2 × d1 × d2, where d1 and d2 are the lengths of the diagonals
= 1/2 × 30 × 16
= 240 cm2

Perimeter of the rhombus = 4a
= 4 × 17
= 68 cm.
33. The perimeter of a rhombus is 60 cm. Of one its diagonals 18 cm long, find
(i) the length of the other diagonals, and
(ii) the area of the rhombus.
Solution
Perimeter of a rhombus = 4a (Here, a is the side of the rhombus)
⇒ 60 = 4a
⇒ a = 15 cm
(i) Given:
One of the diagonals is 18 cm long
d1 = 18 cm
Thus we have:

∴ Length of the other diagonal = 24 cm
(ii) Area of the rhombus = 1/2 × d1 × d2
= 1/2 × 18 × 24
= 216 cm2
34. The area of rhombus is 480 cm2, and one of its diagonal measures 48 cm. Find
(i) the length of the other diagonal.
(ii) the length of each of the sides
(iii) its perimeter
Solution
(i) Area of a rhombus, 1/2 × d1 × d2, where d1 and d2 are the lengths of the diagonals.
⇒ 480 = 1/2 × 48 × d2
⇒ d2 = (480 × 2)/48
⇒ d2 = 20 cm
∴ Length of the other diagonal = 26 cm
(ii)

(iii) Perimeter of the rhombus = 4 × Side
= 4 × 26
= 104 cm
35. The parallel sides of trapezium are 12 cm and 9 cm and the distance between them is 8 cm. Find the area of the trapezium.
Solution
Area of the trapezium = 1/2 × (sum of the parallel sides) × distance between the parallel sides
= 1/2 × (12 + 9) × 8
= 21 × 4
= 84 cm2
So, the area of the trapezium is 84 cm2.
36. The shape of the cross section of a canal is a trapezium. If the canal is 10 m wide at the top, 6 m wide at the bottom and the area of its cross section is 640 m2, find the depth of the canal.
Solution

Area of trapezium = 1/2 × (Sum of parallel sides) × (Distance between them)
⇒ 640 = 1/2 × (10 + 6) × h
⇒ 1280/16 = h
⇒ h = 80 m
Therefore, the depth of the canal is 80 m.
37. Find the area of trapezium whose parallel sides are 11 m and 25 m long, and the nonparallel sides are 15 m and 13 m long.
Solution

The opposite sides of quadrilateral DEBC are parallel. Hence, DEBC is a parallelogram
∴ DE = BC = 13 m
Also,
AE = (AB – EB) = (AB – DC)
= (25 – 11)
= 14 m
For ∆DAE:
Let:
AE = a = 14 m
DE = b = 13 m
DA = c = 15 m
Thus, we have:
s = (a + b + c)/2
s = (14 + 13 + 15)/2 = 21 m
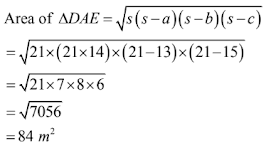
Area of ∆DAE = 1/2 × AE × DL
⇒ 84 = 1/2 × 14 × DL
⇒ (84 × 2)/14 = DL
⇒ DL = 12 m
Area of trapezium = 1/2 × (Sum of parallel sides) × (Distance between them)
= 1/2 × (11 + 25) × 12
= 1/2 × 36 × 12
= 216 m2
Exercise - Formative Assessment
1. In the given figure ABCD is a quadrilateral in which ∠ABC = 90°, AC = 17 cm, BC = 15 cm, BD = 12 cm and CD = 9 cm. The area of quadrilateral ABCD is

(b) 114 cm2
(c) 95 cm2
(d) 57 cm2
Solution
(b) 114 cm2
Using Pythagoras theorem in ∆ABC, we get:
AC2 = AB2 + BC2

= 8 cm
Area of ∆ABC = 1/2 × AB × BC
= 1/2 × 8 × 15
= 60 cm2
Area of ∆ABC = 1/2 × BD × CD
= 1/2 × 12 × 9
= 54 cm2
∴ Area of quadrilateral ABCD = Ar(∆ABC) + Ar(∆BCD)
= 54 + 60
= 114 cm2
2. In the given figure ABCD is a trapezium in which AB = 40 m, BC = 15 m, CD = 28 m, AD = 9 m and CE ⟂AB. Area of trapezium ABCD is

(b) 316 m2
(c) 296 m2
(d) 284 m2
Solution
(a) 306 m2
In the given figure, AECD is a rectangle.
Length AE = Length CD = 28 m
Now,
BE = AB – AE
= 40 – 28
= 12 m
Also,
AD = CE = 9 m
Area of trapezium = 1/2 × sum of parallel sides × Distance between them
= 1/2 × (DC + AB) × CE
= 1/2 × (28 + 40) × 9
= 1/2 × 68 × 9
= 306 m2
In the given figure, if DA is perpendicular to AE, then it can be solved, otherwise it cannot be solved.
3. The sides of a triangle are in the ratio 12 : 14: 25 and its perimeter is 25.5 cm. The largest side of the triangle is
(a) 7 cm
(b) 14 cm
(c) 12.5 cm
(d) 18 cm
Solution
(c) 12.5 cm
Let the sides of the triangle be 12x cm, 14x cm, and 25x cm
Thus, we have
Perimeter = 12x + 14x + 25x
⇒ 25.5 = 51x
⇒ x = 25.5/51 = 0.5
∴ Greatest side of the triangle 25x
= 25 × 0.5
= 12.5 cm
4. The parallel sides of a trapezium are 9.7 cm and 6.3 cm, and the distance between them is 6.5 cm. The area of the trapezium is
(a) 104 cm2
(b) 78 cm2
(c) 52 cm2
(d) 65 cm2
Solution
(c) 52 cm2
Area of trapezium = 1/2(Sum of parallel sides) × Distance between them
= 1/2 × (9.7 + 6.3) × 6.5
= 8 × 6.5
= 52.0 cm2
5. Find the area of an equilateral triangle having each side of length 10 cm. (Take √3 = 1.732)
Solution
Given:
Side of the equilateral triangle = 10 cm
Thus, we have:
Area of the equilateral triangle = √3/4 side2
= √3/4 × 10 × 10
= 25 × 1.732
= 43.3 cm2
6. Find the area of an isosceles triangle each of whose equal sides is 13 cm and whose base is base is 24 cm.
Solution
Area of an isosceles triangle:
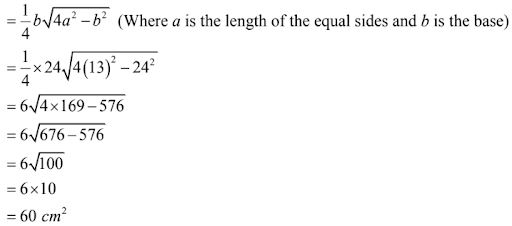
7. The longer side of a rectangular hall is 24 m and the length of its diagonal is 26 m. Find the area of hall.
Solution
Let the rectangle ABCD represent the hall.

Using the Pythagoras theorem in the right-angled triangle ABC, we have
Diagonal2 = Length2 + Breadth2

∴ Area of the hall = Length × Breadth
= 24 × 10
= 240 m2
8. The length of the diagonal of a square is 24 cm. Find its area.
Solution
The diagonal of a square forms the hypotenuse of an isosceles right triangle. The other two sides are the sides of the square of length a cm.
Using Pythagoras theorem, we have:
Diagonal2 = a2 + a2 = 2a2
⇒ Diagonal = √2a
Diagonal of the square = 2√a
⇒ 24 = √2a
⇒ a = 24/√2
Area of the square = Side2 = (24/√2)2
= (24 × 24)/2
= 288 cm2
9. Find the area of a rhombus whose diagonals are 48 cm and 20 cm long.
Solution
Area of the rhombus = 1/2(Product of diagonal)
= 1/2(48 × 20)
= 480 cm2
10. Find the area of a triangle whose sides are 42 cm, 34 cm and 20 cm.
Solution
To find the area of the triangle, we will first find the semi-perimeter of the triangle
Thus, we have:
s = 1/2(a + b + c) = 1/2(42 + 34 + 20)
= 1/2 × 96
= 48 cm
Now,

Solution
Let the length and breadth of the lawn be 5x and 3x m, respectively.
Now,
Area of the lawn = 5x × 3x = 5x2

Length = 5x = 5 × 15 = 75 m
Breadth = 3x = 3 × 15 = 45 m
∴ Perimeter of the lawn = 2(Length + breadth)
= 2(75 + 45)
= 2 × 120
= 240 m
Total cost of fencing the lawn at Rs 20 per meter = 240 × 20
= Rs 4800
12. Find the area of a rhombus each side of which measures 20 cm and one of whose diagonals is 24 cm.
Solution
Given:
Sides are 20 cm each and one diagonal is of 24 cm.
The diagonal divides the rhombus into two congruent triangles, as shown in the figure below.

We will now use Hero’s formula to find the area of triangle ABC.
First, we will find three semi-perimeter.
s = 1/(a + b + c)
= 1/2(20 + 20 + 24)
= 64/2
= 32 m

Now,
Area of the rhombus = 2 × Area of triangle ABC = 192 × 2
= 384 cm2
13. Find the area of a trapezium whose parallel sides are 11 cm and 25 cm long and non-parallel sides are 15 cm and 13 cm.
Solution
We will divide the trapezium into a triangle and a parallelogram
Difference in the lengths of parallel sides = 25 – 11 = 14 cm
We can represent this in the following figure:

Trapezium ABCD is divide into parallelogram AECD and triangle CEB.
Consider triangle CEB.
In triangle CEB, we have,
EB = 25 – 11 = 14 cm
Using Hero’s theorem, we will first evaluate the semi-perimeter of triangle CEB and then evaluate its area.
Semi-perimeter s = 1/2 (a + b + c) = 1/2(15 + 13 + 14)
= 42/2
= 21 cm

Area of triangle CEB = 1/2(Base × height)
Height of triangle CEB = (Area × 2)/Base
= (84 × 2)/14
= 12 cm
Consider parallelogram AECD.
Area of parallelogram AECD = Height × Base = AE × CF
= 12 × 11
= 132 cm2
Area of trapezium ABCD = Ar(∆BEC) + Ar(parallelogram AECD)
= 132 + 84
= 216 cm2
14. The adjacent sides of a ||gm ABCD measure 34 cm and 20 cm and the diagonal AC is 42 cm long. Find the area of the ||gm.

The diagonal of a parallelogram divides it into two congruent triangles. Also, the area of the parallelogram is the sum of the areas of the triangles.
We will now use Hero’s formula to calculate the area of triangle ABC.
Semi-perimeter, s = 1/2(34 + 20 + 42) = 1/2(96) = 48 cm
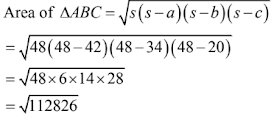
Area of the parallelogram = 2 × Area ∆ABC
= 2 × 336
= 672 cm2
15. The cost of fencing a square lawn at 14 per metre is 2800. Find the cost of mowing the lawn at ₹54 per 100 m2.
Solution
Given:
Cost of fencing = Rs 2800
Rate of fencing = Rs 14
Now,
Perimeter = (Total cost)/Rate
= 2800/14
= 200 m
Because the lawn is square, its perimeter is 4a, where a is the side of the square)
⇒ 4a = 200
⇒ a = 200/4
= 50 m
Area of the lawn = Side2 = 502 = 2500 m2
Cost for mowing the lawn per 100m2 = Rs 54
Cost for mowing the lawn per 1 m2 = Rs 54/100
Total cost for mowing the lawn per 2500 m2 = 54/100 × 2500
= Rs 1350
16. Find the area of quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diagram BD = 20 cm.

Quadrilateral ABCD is divided into triangles ∆ABD and ∆BCD.
We will now use Hero’s formula
For ∆ABD:
Semi-perimeter, s = 1/2(42 + 30 + 34) = 96/2 = 48 cm

Area of quadrilateral ABCD = Ar(∆ABD) + Ar(BDC)
= 336 + 210
= 546 cm2
17. A parallelogram and a rhombus are equal in area. The diagonals of the rhombus measure 120 m and 44 m. If one of the sides of the ||gm is 66 m long, find its corresponding altitude.
Solution
Area of the rhombus = 1/2(Product of diagonals)
= 1/2(120 × 44)
= 2640 m2
Area of the parallelogram = Base × Height
= 66 × Height
Given:
The area of the rhombus is equal to the area of the parallelogram.
Thus, we have:
66 × Height = 2640
⇒ Height = 2640/66
= 40 m
∴ Corresponding height of the parallelogram = 40 m
18. The diagonals of a rhombus are 48 cm and 20 cm long. Find the perimeter of the rhombus.
Solution
Diagonals of a rhombus perpendicularly bisect each other. The statement can help us find a side of the rhombus. Consider the following figure.

ABCD is the rhombus and AC and AD are the diagonals. The diagonals intersect at point O.
We know
∠DOC = 90°
DO = OB = 1/2 DB = 1/2 × 48 = 24 cm
Similarly,
AO = OC = 1/2 AC = 1/2 × 20
= 10 cm
Using Pythagoras theorem in the right angled triangle ∆DOC, we get

DC is a side of the rhombus
We know that in a rhombus, all sides are equal.
∴ Perimeter of ABCD = 26 × 4
= 104 cm
19. The adjacent sides of parallelogram are 36 cm and 27 cm in length. If the distance between the shorter sides is 12 cm, find the distance between the longer sides.
Solution

∴ AB × DE = BC × DF
⇒ DE = (BC × DF)/AB
= (27 × 12)/36
= 9 cm
∴ Distance between the longer sides = 9 cm
20. In a four-sided field, the length of the longer diagonal is 128 m. The lengths of perpendiculars from the opposite vertices upon this diagonal are 22.7 m and 17.3 m. Find the area of the field.
Solution
The field, which is represented as ABCD, is given below

The area of the field is the sum of the areas of triangles ABC and ADC.
Area of triangle ABC = 1/2(AC × BF) = 1/2(128 × 22.7) = 1452.8 m2
Area of the triangle ADC = 1/2(AC × DE) = 1/2(128 × 17.3) = 1107.2 m2
Area of the field = Sum of the areas of both the triangles = 1452.8 + 1107.2 = 2560 m2
