Chapter 17 Perimeter and Area of Plane Figures RS Aggarwal Solutions Exercise 17A Class 10 Maths

Chapter Name | RS Aggarwal Chapter 17 Perimeter and Area of Plane Figures |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Perimeter and Area of Plane Figures Exercise 17A Solutions
1. Find the area of triangle whose base measure 24 cm and the corresponding height measure 14.5 cm.
Solution
Given: base = 24 cm, corresponding height = 14.5 cm
Area of a triangle = 1/2 × base × corresponding height
= 1/2 × 24 × 14.5
= 174 cm2
2. Find the areas of the triangle whose sides are 42 cm, 34 cm and 20 cm. Also, find the height corresponding to the longest side.
Solution
Let the sides of the triangle be a = 20 cm, b = 34 cm and c = 42 cm
Let s be the semi-perimeter of the triangle.
s = 1/2(a + b + c)
s = 1/2(20 + 34 + 42)
s = 48 cm

Area of a triangle = 1/2 × b × h
⇒ 336 = 1/2 × 42 × h
⇒ 672 = 42h
⇒ 672/42 = h
⇒ h = 16 cm
The height corresponding to the longest side is 16 cm.
3. Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also, find the height corresponding to the smallest side.
Solution
Let the sides of triangle be a = 18 cm, b = 24 cm and c = 30 cm
Let s be the semi-perimeter of the triangle.
s = 1/2(a + b + c)
s = 1/2(18 + 24 + 30)
s = 36 cm
The smallest side is 18 cm long. This is the base.
Now, area of a triangle = 1/2 × b × h
⇒ 216 = 1/2 × 18 × h
⇒ 216 = 9h
⇒ 216/9 = h
⇒ h = 24 cm
The height corresponding to the smallest side is 24 cm.
4. The sides of a triangle are in the ratio 5 : 12 : 13 and its perimeter is 150 m. Find the area of the triangle.
Solution
Let the sides of a triangle be 5x m, 12x m and 13x m.
Since, perimeter is the sum of all the sides,
5x + 12x + 13x = 150
⇒ 30x = 150
Or, x = 150/30 = 5
The lengths of the sides are:
a = 5 × 5 = 25 m
b = 12 × 5 = 60 m
c = 13 × 5 = 65 m

Solution
Let the sides of the triangular field be 25x, 17x and 12x.
As, perimeter = 540 m
⇒ 25x + 17x + 12x = 540
⇒ 54x = 540
⇒ x = 540/54
⇒ x = 10
So, the sides are 250 m, 170 m and 120 m.
Now, semi-perimeter, s = (250 + 170 + 120)/2 = 540/2 = 270 m

Also, the cost of ploughing field = (9000 × 40)/100
= 3,600
6. The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find its area of the triangle.
Solution
The perimeter of a right-angled triangle = 40 cm
Therefore, a + b + c = 40 cm
Hypotenuse = 17 cm
Therefore, c = 17 cm
a + b + c = 40 cm
⇒ a + b + 17 = 40
⇒ a + b = 23
⇒ b = 23 – a …(i)
Now, using Pythagoras theorem, we have:
a2 + b2 = c2
⇒ a2 + (23 – a)2 = 172
⇒ a2 + 529 – 46a + a2 = 289
⇒ 2a2 – 46a + 529 – 289 = 0
⇒ 2a2 – 46a + 240 = 0
⇒ a2 – 23a + 120 = 0
⇒ (a – 15)(a – 8) = 0
⇒ a = 15 or a = 8
Substituting the value of a = 15, in equation (i) we get:
b = 23 – a
= 23 – 15
= 8 cm
If we had chosen a = 8 cm, then, b = 23 – 8 = 15 cm
In any case,
Area of triangle = 1/2 × base × height
= ½ × 8 × 15
= 60 cm2
7. The difference between the sides at the right angles in a right-angled triangle is 7 cm. The area of the triangle is 60 cm2. Find its perimeter.
Solution
Area of the triangle = 60 cm2
Let the sides of the triangle be a, b and c, where a is the height, b is the base and c is hypotenuse of the triangle.
a – b = 7 cm
a = 7 + b …(1)
Area of triangle = 1/2 × b × h
⇒ 60 = 1/2 × b × (7 + b)
⇒ 120 = 7b + b2
⇒ b2 + 7b – 120 = 0
⇒ (b + 15)(b – 8) = 0
⇒ b = - 15 or 8
Side of a triangle cannot be negative.
Therefore, b = 8 cm
Substituting the value of b = 8 cm, in equation (1):
a = 7 + 8 = 15 cm
Now, a = 15 cm, b = 8 cm
Now, in the given right triangle, we have to find third side.
(Hypotenuse)2 = (First side)2 + (Second side)2
⇒ Hypontenuse2 = 82 + 152
⇒ Hypotenuse2 = 64 + 225
⇒ Hypotenuse2 = 289
⇒ Hypotenuse = 17 cm
So, the third side is 17 cm.
Perimeter of a triangle = a + b + c.
Therefore, required perimeter of the triangle 15 + 8 + 1740 cm
8. The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24 cm2, find the perimeter of the triangle.
Solution
Given:
Area of triangle = 24 cm2
Let the sides be a and b, where a is the height and b is the base of triangle
a – b = 12 cm
a = 2 + b ….(1)
Area of triangle = 1/2 × b × h
⇒ 24 = ½ × b × (2 + b)
⇒ 48 = b + 1/2b2
⇒ 48 = b + 1/2,.b2
⇒ 48 = 2b + b2
⇒ b2 + 2b – 48 = 0
⇒ (b + 8)(b – 6) = 0
⇒ b = -8 or 6
Side of a triangle cannot be negative.
Therefore, b = 6 cm
Substituting the value of b = 6 cm in equation (1), we get:
a = 2 + 6 = 8 cm
Now, a = 8 cm, b = 6 cm
In the given right triangle we have to find third side. Using the relation
(Hypotenuse)2 = (Oneside)2 + (Otherside)2
⇒ Hyp2 = 82 + 62
⇒ Hyp2 = 64 + 36
⇒ Hyp2 = 100
⇒ Hyp2 = 100
⇒ Hyp = 10 cm
So, the side is 10 cm
So, perimeter of the triangle = a + b + c
= 8 + 6 + 10
= 24 cm
9. Each side of an equilateral triangle is 10 cm. Find
(i) area of the triangle and
(ii) the height of the triangle
Solution
(i) The area of the equilateral triangle = √3/4 × side2
= √3/4 × 102
= √3/4 × 100
= 25√3 cm2
Or 25 × 1.732 = 43.3 cm2
So, the area of the triangle is 25√3 cm2 or 43.3 cm2.
(ii) As, area of the equilateral triangle = 25√3 cm2
⇒ 1/2 × Base × Height = 25√3
⇒ 1/2 × 10 × Height = 25√3
⇒ 5 × height = 25√3
⇒ Height = (25√3)/2 = 5√3
Or height = 5 × 1.732 = 8.6 m
∴ The height of the triangle is 5√3 cm or 8.66 cm.
10. The height of an equilateral triangle is 6 cm. Find its area.
Solution
Let the side of the equilateral triangle be x cm.
As, the area of an equilateral triangle = √3/4(side)2 = x2√3/4
Also, the area of the triangle = 1/2 × Base × Height
= 1/2 × x × 6
= 3x
So, (x2√3)/4 = 3x
⇒ (x√3)/4 = 3
⇒ x = 12/√3
⇒ x = 12/√3 × √3/√3
⇒ x = (12√3)/3
⇒ x = 4√3 cm
Now, area of the equilateral triangle = 3x
= 3 × 4√3
= 12√3
= 12 × 1.73
= 20.76 cm2
11. If the area of an equilateral triangle is 36√3 cm2, find its perimeter.
Solution
Area of equilateral triangle = 36√3 cm2
Area of equilateral triangle = (√3/4 × a2), where a is the length of the side
⇒ 36√3 = √3/4 × a2
⇒ 144 = a2
⇒ a = 12 cm
Perimeter of a triangle = 3a
= 3 × 12
= 36 cm
12. If the area of an equilateral triangle is 81√3 cm2. Find its height.
Solution
Area of equilateral triangle = 81√3 cm2
Area of equilateral triangle = (√3/4 × a2), where a is the length of the side
⇒ 81√3 = √3/4 × a2
⇒ 324 = a2
⇒ a = 18 cm
Height of triangle = √3/2 × a
= √3/2 × 18
= 9√3 cm
13. The base of a right-angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
Solution
Base = 48 cm
Hypotenuse = 50 cm
First we will find the height of the triangle; let the height be ‘p’.
⇒ (Hypotenuse)2 = (base)2 + p2
⇒ 502 = 482 + p2
⇒ p2 = 502 – 482
⇒ p2 = (50 – 48)(50 + 48)
⇒ p2 = 2 × 98
⇒ p2 = 196
⇒ p = 14 cm
Area of the triangle = 1/2 × base × height
= 1/2 × 48 × 14
= 336 cm2
14. The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
Solution
Hypotenuse = 65 cm
Base = 60 cm
In a right-angled triangle,
(Hypotenuse)2 = (Base)2 + (perpendicular)2
⇒ (65)2 = (60)2 + (perpendicular)2
⇒ (65)2 – (60)2 + (perpendicular)2
⇒ (perpendicular)2 = (65 – 60)(65 + 60)
⇒ (perpendicular)2 = 5 × 125
⇒ (perpendicular)2 = 625
⇒ (perpendicular)2 = 25 cm
Area of triangle = 1/2 × base × perpendicular
= 1/2 × 60 × 25
= 750 cm2
15. Find the area of a right –angled triangle, the radius of whose, circumference measures 8 cm and the altitude drawn to the hypotenuse measures 6 cm.
Solution

Height = 6 cm
Area = ?
In a right angled triangle, the center of the circumference is the midpoint of the hypotenuse.
Hypotenuse = 2 × (radius of circumference) for a right triangle)
= 2 × 8
= 16 cm
So, hypotenuse = 16 cm
Now, base = 16 cm and height = 6 cm
Area of the triangle = 1/2 × base × height
= ½ × 16 × 6
= 48 cm2
16. Find the length of the hypotenuse of an isosceles right-angled triangle whose area is 200 cm2. Also, find its perimeter.
Solution
In a right triangle, base = height = a
Therefore,
Area of a triangle = 1/2 × base × height = 1/2 × a × a = 1/2.a2
Further, given that the area of the isosceles right triangle = 200 cm2

= 20 × 1.41
= 28.2 cm
Perimeter of the triangle = a + a + c
= 20 + 20 + 28.2
= 68.2 cm
The length of the hypotenuse is 28.2 cm and the perimeter of the triangle is 68.2 cm.
17. The base of an isosceles triangle measure 80 cm and its area is 360 cm2. Find the perimeter of the triangle.
Solution
Given:
Base = 80 cm
Area = 360 cm2
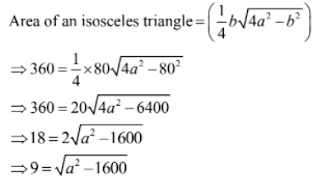
Squaring both the sides, we get:
⇒ 81 = a2 – 1600
⇒ a2 = 1681
⇒ a = 41 cm
Perimeter = (2a + b)
= [2(41) + 80]
= 82 + 80
= 162 cm
So, the perimeter of the triangle is 162 cm.
18. Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
Solution
Let the height of the triangle be h cm.
Each of the equal sides measures a = (h + 2) cm and b = 12 cm (base)
Now,
Area of the triangle = Area of the isosceles triangle

On squaring both the sides, we get:
⇒ 4h2 = 4h2 + 16h + 16 – 144
⇒ 16h – 128 = 0
⇒ h = 8
Area of the triangle = 1/2 × b × h
= 1/2 × 12 × 8
= 48 cm2
19. Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10 cm.
Solution
Length of each of the equal sides of the isosceles right-angled triangle = a = 10 cm
And,
Base = height = a
Area of isosceles right –angled triangle = ½ × Base × Height
The hypotenuse of an isosceles right-angled triangle can be obtained using Pythagoras theorem
If h denotes the hypotenuse, we have:
h2 = a2 + a2
⇒ h = 2a2
⇒ h = √2a
⇒ h = 10√2 cm
∴ Perimeter of the isosceles right-angled triangle = 2a + √2a
= 2 × 10 + 1.41 × 10
= 20 + 14.1
= 34.1 cm
20. In the given figure, △ABC is an equilateral triangle the length of whose side is equal to 10 cm, and △ADC is right-angled at D and BD = 8 cm. Find the area of the shaded region.

Given:
Side if equilateral triangle ABC = 10 cm
BD = 8 cm
Area of equilateral △ABC = √3/4.a2 (where a = 10 cm)
Area of equilateral △ABC = √3/4 × 102
= 25√3
= 25 × 1.732
= 43.30 cm2
In the right △BDC, we have,
BC2 = BD2 + CD2
⇒ 102 = 82 + CD2
⇒ CD2 = 102 – 82
⇒ CD2 = 36
⇒ CD = 6
Area of triangle △BCD = 1/2 × b × h
= ½ × 8 × 6
= 24 cm2
Area of the shaded region = Area of △ABC – Area of △BDC
= 43.30 – 24
= 19.3 cm2

