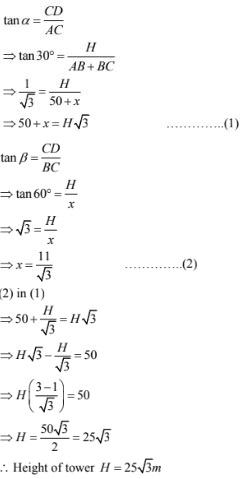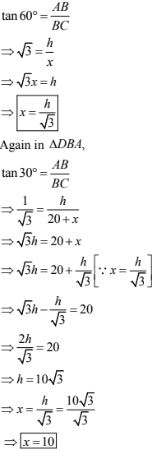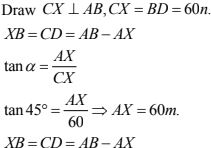RD Sharma Solutions for Class 10 Chapter 12 Trigonometry Exercise 12.1

RD Sharma Solutions Chapter 12 Trigonometry Exercise 12.1 Class 10 Maths

Chapter Name	RD Sharma Chapter 12 Trigonometry
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	No Other Exercises
Related Study	NCERT Solutions for Class 10 Maths

Exercise 12.1 Solutions

1. A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower ? 

Solution

Given,
Distance between point of observation and foot of tower = 20m = BC 
Angle of elevation of top of tower = 60° = 0 
Height of tower H = ? = AB 

2. The angle of elevation of a ladder leaning against a wall is 600 and the foot of the ladder is 9.5m away from the wall. Find the length of the ladder. 

Solution

3. A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2m away from the wall and the ladder is making an angle of 600 with the level of the ground. Determine the height of the wall.

Solution

Distance between foot and ladder and wall = 2m = BC 
Angle made by ladder with ground θ = 60°
Height of wall H = ? = AB 
Now fig ABC forms a right angled triangle 

4. An electric pole is 10m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole up right. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire. 

Solution

Height of the electric pole H = 10 m  = AB angle made by steel wire with ground 
(horizontal) θ = 45° 
Let length of rope wire = l = AC 
If we represent above data is 
Form of figure thin it forms a right triangle ABC 

5. A kite is flying at a height of 75 meters from the ground level, attached to a string inclined at 600 to the horizontal. Find the length of the string to the nearest meter. 

Solution

Given 
Height o kite from ground  = 75 m = AB 
Inclination of string with ground 
θ = 60°

Length of string l = ? = AC 
If we represent the above data is form of figure as shown then its form a right angled triangle ABC here 

6. The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O  = 15/8, how high is the kite ? 

Assume that there is no slack in the string. 

Solution

Length of string between point on ground and kite = 90 
Angle made by string with ground is θ and tan θ = 15/8 

7. A vertical tower stands on a horizontal plane and is surmounted by a vertical flag - staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flag - staff are respectively 600 and 45°. Find the height of the flag - staff and that of the tower. 

Solution

Given,
Vertical tower is surmounted by flag staff distance between tower and observer = 70 m = BC. Angle of elevation of top of tower α = 45°
Angle of elevation of top of flag staff  β = 60°

Height of flagstaff = h = AD 
Height of tower = H = AB 
If we represent the above data in the figure then it forms right angled triangles ΔABC and ΔCBD 
When θ is angle in right angle triangle we know that 

8.  A vertically straight tree, 15m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break ?

Solution

Initial height of tree H = 15 m = AB 
Let us assume that it is broken at pointe. 

Then given that angle made by broken part with ground θ = 60°
Height from ground to broken pointe = h = BC 
AB = AC + BC 
⇒ H = AC + h ⇒ AC = (H - h) m 
If we represent the above data in the figure as shown then it forms right angled triangle ABC from fig 

9. A vertical tower stands on a horizontal plane and is surmounted by a vertical flag - staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag -staff are respectively 30° and 60° . Find the height of the tower. 

Solution

Height of the flagstaff  h = 5m  = AP 
Angle of elevation of the top of flagstaff = 60° = α
Angle of elevation of the bottom of flagstaff = 30° = β
Let height of tower be Hm = AB. 
If we represent the above data in forms of figure then it from triangle CBD in which ABC is included with ∠B = 90°

In right angle triangle, if 
Angle is θ then 

10. A person observed the angle of elevation of the top of a tower as 30° . He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60° . Find the height of the tower. 

Solution

Given, 
Angle of elevation of top of tour, from first point of elevation (A) α = 30°
Let the walked 50 m from first point (A) to B then AB = 50 m 
Angle of elevation from second point B ⇒ Gb  = 60° 
Now let is represent the given data in form of then it forms triangle ACD with triangle BCD in it ∠c = 90° 
Let height of tower, be 
Hm = CD 
BC = xm. 
If in a right angle triangle θ is the angle then tan θ = Opposite side/Adjacent side 

11. The shadow of a tower, when the angle of elevation of the sun is 45° , is found to be 10 m longer than when it was 60° . Find the height of the tower .

Solution

Let the length of shadow of tower when angle of elevation is (α = 60°) be x m = BC then according to problem 
Length of the shadow with angle of elevation (β = 45°) is (10 + x)m = BD. 
If we represent the , above data in form of figure then it forms a triangle ABD is which triangle ABC is included with ∠B = 90° 
Let height of  tower be H m = AB  
If in right angle triangle one of the angle is θ then 
tan θ = Opposite side/Adjacent side 

∴ Height of tower = 23.66 m 

12. A parachutist is descending vertically and makes angles of elevation of 45° and  60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of he point where he falls on the ground from the just observation point. 

Solution

Let is the parachutist at highest point A. Let C and D be points which are 100 m a part on ground where from then CD = 100m 

Angle of elevation from point C = 45° [α]
Angle of elevation from point B = 60° [β] 
Let B be the point just vertically down the parachute 
Let us draw figure according to above data then it forms the figure as shown in which ABC is triangle and ABD included in it with 
ABD triangle included 

Maximum height of parachute 
From ground = AB = H m 
Distance of point where parachute falls to just nearest observation point = xm 
If in right angle triangle one of the included angle θ. Then 
tan θ = Opposite side /Adjacent side 

Maximum height of parachute from ground H = 236.6 m 
Distance between point where parachute falls on ground and just observation is x = 136.6 m 

13. On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60° . If the height of the tower is 150 m, find the distance between the objects. 

Solution

14. The angle of elevation of a tower from a point on the same level as the foot of the tower is 30° . On advancing 150 meters towards the foot of the tower, the angle of elevation of the tower becomes 60° . Show that the height of the tower is 129.9 meters (Use √3 = 1.732). 

Solution

Angle of elevation of top of tower from first point A, α = 30°

Let we advanced through A to b by 150m then AB = 150 m 
Angle of elevation of top of lower from second point  B, β = 60° 
Let height of tower CD = H m 
If we represent the above data in from of figure then it forms figure as shown with ∠D = 90°

If in right angled triangle, one of included angle is θ then tan θ = Opposite side/Adjacent side 

15. The angle of elevation of the top of a tower as observed from a point in a horizontal plane through the foot of the tower is 32° . When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to  be 63° . Find the height of the tower and the distance of the first position form the tower. [ Take tan 32° = 0.6248 and tan 63° = 1.9626] 

Solution

Let h be height of tower and the angle of elevation as observed from the foot of tower is 32° and observed move towards the tower with distance 100 m then angle of elevation becomes 63°.

Let BC = x and CD = 100

Now we have to find height of tower

So we use trigonometrical ratios.

In a triangle ABC,

So distance of the first position from the tower is = 100 + 46.7 = 146.7 m

Hence the height of tower is 91.66 m and the desires distance is 146.7 m.

16. The angle of elevation of the top of a tower from a point A on the ground is 30° . Moving a distance of 20 metres towards the foot of the tower to a point B the angle of elevation increases to  60° . Find the height of the tower & the distance of the tower from the point A. 

Solution

Angle of elevation of top of tower from points A α = 30° 
Angle of elevation of top of tower from points B β = 60°

Distance between A and B, AB = 20 m 

Let height of tower CD = 'h' m 
Distance between second point B from foot of tower bc 'x' m .
If we represent the above data in the figure, then it forms figure as shown with ∠D = 90°
In right angled triangle if one of the included angle is θ then tan θ = Opposite side/Adjacent side 

17. From the top of a building 15 m high the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60° . Find the height of the tower and the distance between the tower and building. 

Solution

Let AB be the building and CD be the tower height of the building is 15m = h = AB. 
Angle of elevation of top of tower from tp of building α = 30°
Angle of elevation of top of tower from bottom of building β = 60°

Distance between tower and building BD = x 
Let height of tower above building be 'a' m 
If we represent the above data is from of figure then it forms figure as shown with 
∠D = 90° also draw AX||BD, ∠AXC = 90° 

Here ABDX is a rectangle 
∴ BD = DX = 'x'm 
AB = XD = h = 15m 
In right triangle if one of the included angle is θ then tan θ = Opposite side/Adjacent side 

= 7.5 × 1.732 
Height of tower above ground = h +a 
= 15 + 7.5 = 22. 5 m 
Distance between tower and building = 12.99 m  

18. On a horizontal plane there is a vertical tower with a flag pole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flag pole are 60° and 30° respectively. Find the height of the tower and the flag pole mounted on it. 

Solution

Let AB be the tower and BC be flagstaff on the tower 
Distance of point of observation from foot of tower BD = 9m 
Angle of elevation of top of flagstaff [c] α = 60°
Angle of elevation of bottom of flag pole [B] β = 30°
Let height of tower = 'x' = AB 
Height of pole = 'y' = BC 
The above data is represented in form of figure a shown with ∠A = 90°
If in right triangle one of the included is θ, then 

tan θ = Opposite side/Adjacent side 

19. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. 

Solution

Let initially tree height be AB 
Let us assumed that the tree is broken at point C
Angle made by broken part CB' with ground is 30° = θ
Distance between foot of tree of point where it touches ground B'A = 8m 
Height  of tree = h = AC + CB' = AC + CB 
The above information is represent in the form of figure as shown 

cos θ = Adjacent side/Hypotenuse 
tan θ = Opposite side/Adjacent side 

20.  From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag - staff from P is 45° . Find the length of the flag - staff an the distance of the building from the point P . (Take √3 = 1.732). 

Solution

Let AB be the tower and 80 be the flagstaff Angle of elevation of top of building from P α = 30°

AB = height of tower = 10m 
Angle of elevation of top of flagstaff from P   β = 45°
Let height of flagstaff BD = 'a'm 
The above information is represented in form of figure as shown with ∠A = 90° 
In a right angled triangle if one of the included 
Angle is θ 
tan θ = Opposite side/Adjacent side 

21. A 1.6m tall girl stands at a distance of 3.2 m from a lamp - post and casts a shadow of 4.8 m on the ground. Find the height of the lamp - post by using  (i) trigonometric ratios (ii) property of similar triangles. 

Solution

Let AC be the lamp past of height 'h' 
We assume that ED = 1.6m, BE = 4.8m and EC = 3.2 m 
We have to find the height of the lamp post 
Now we have to find height of lamp post using similar triangles 

22. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked toward the building. 

Solution 

Let the boy was standing at point S initially. He walked towards the building and reached at point T.

It can be observed that

PR = PQ - RQ

= (30 - 1.5) m = 28.5 m = 57/2 m

In ΔPAR,

(PR)/(AR) = tan 30º

Hence, he walked 19√3m towards the building.

23. The shadow of a tower standing on a level ground is found to be 40 m longer when Sun's altitude is 30° than when it was 60°. Find the height of the tower 

Solution

Let AB be the tower of height h.

Given the shadow of tower DC = 40 m.

The attitude of the sun is ∠D = 30° and ∠C = 60°. Here we have to find the height of the tower.

Let BC = x and DC= 40.

So we have trigonometric ratios in ΔACB,.

Hence height of tower is 20√3 m

24. From a point on the ground the angles of elevation of the bottom and top of  a transmission tower fixed at the top of 20 m high building are 45° and 60° respectively. Find the height of the transmission tower. 

Solution 

Given height of building = 20 m = AB
Let height of tower above building = 'h' = BC 
Height of tower + building = (h + 20)m [from ground ] = CA 
Angle of elevation of bottom of tour, α = 45°

Angle of elevation of top of tour, β = 60°
Let distance between tower and observation point = 'x' m 
The above data is represented in = AD 
The form of figure as shown in one of the included angle is right angle triangle is a then 
tan θ = Opposite side/Adjacent side 

25. The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance the two buildings. 

Solution

Let height of multistoried building 'h' m = AB 
Height of tall building = 8m  = CD 
Angle of depression of top of tall building α = 30°

Angle of depression of bottom of tall building β = 45°

Distance between two building = 'x' m = BD 
Let Ax = x 
AB = AX + XB but XB = CD [∵ AXCD is rectangle]
AB = 'a' m + 8m 
AB = (a + 8)m 
The above information is represented in the form of figure as shown 
If in right triangle are of included angle is θ Then 

tan θ = Opposite side/Adjacent side 

26. A statue 1.6 m tall stands on the top of pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal. 

Solution

Let height of pedestal be 'h' m 
Height of status = 1.6 m 
Angle of elevation of top of status α = 60°
Angle of elevation of pedestal of status α = 60° 
The above data is represented in the form of figure as shown. 
If in right angle triangle one of the included angle is θ then 
tan θ = Opposite side/Adjacent side 

27. A T.V. Tower stands vertically on a bank of a river. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60° . From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30° . find the height of the tower and the width of the river. 

Solution

Let AB be the T.V tower of height 'h' m on a bank of river and 'D' be the point on the opposite of the river. An angle of elevation at top of tower is 60° and form the point 20m away them angle of elevation of tower at the same point is 30° 
Let AB = h and BC = x 
Here we have to find height and width of river the corresponding figure is here 
In ΔCAB, 

Hence the height of the tower is 10√3 m and width of the river is 10m. 

28. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45° . Determine the height of the tower. 

Solution

Given,
Height of building  = 7m = AB 
Height of cable tower = 'H' m = CD
Angle of elevation of top of tower, from top of building α = 60°

Angle of depression of bottom of tower, from top of building β = 45°

The above data is represented in form of figure as shown 

Let CX = 'x' m 
CD = DX + XC = 7m + 'x' m 
= x + 7 m. 
In ΔADX 
tan 45° = Opposite side(XD)/Adjacent side(AX)

29. As observed from the top of a 75 m tall lighthouse, the angle of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. 

Solution

Given 
Height of light house = 75 m = 'h'm = AB 
Angle of depression of ship 1 α = 30°
Angle of depression of ship 2 β = 45°
The above data is represented in form of figure as shown. 
Let distance between ships be 'x' m = CD 
In right triangle if one of included angle is θ then 

tan θ = Opposite side/Adjacent side 

30. The angle of elevation of the top of the building from the foot of the tower is  30° and the angle of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building . 

Solution

Angle of elevation of top of building from foot of tower = 30° = α

Angle of elevation of top of tower, from foot of building = 60° = β
Height of tower = 50 m = AB 
Height of building = 'h' m  = CD 
The above information is represented in form of figure as shown 
In right triangle if one of the included angle is θ then 
tan θ = Opposite side/Adjacent side 

31. From a point on a bridge across a river the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If bridge is at the height of 30 m from the banks, find the width of the river. 

Solution 

Height of the bridge = 30m[AB] 
Angle of depression of bank 1 i.e., α = 30° [B₁]
Angle of depression of bank 2 i.e., β = 30° [B₂]

Given banks are on opposite sides 
Distance between banks B₁B₂ = B₁B + BB₂] 
The above information is represented is the form of figure as shown in right angle triangle if one of the included angle is O then 
tan θ = Opposite side/Adjacent side 

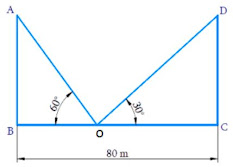
32. Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles. 

Solution

Let us consider the two poles of equal heights as AB and DC and the distance between the poles as BC.

From the point O, between the poles on the road, the angle of elevation of the top of the poles AB and CD are 60° and 30° respectively.

Trigonometric ratio involving angles, distance between poles and heights of poles is tan θ.

Let the height of the poles be x

Therefore AB = DC = x

In ΔAOB,

tan 60° = AB/BO

√3 = x / BO

BO = x / √3 ....(i)

In ΔOCD,

tan 30° = DC / OC

⇒ 1/√3 = x/(BC - OB)

⇒ 1/√3 = x/(80 - x/√3) [from (i)]

⇒ 80 - x/√3 = √3x

⇒ x/√3 + √3x = 80

⇒ x (1/√3 + √3) = 80

⇒ x (1 + 3) / √3 = 80

⇒ x (4/√3) = 80

⇒ x = 80√3 / 4

⇒ x = 20√3

Height of the poles x = 20√3 m.

Distance of the point O from the pole AB

BO = x/√3

= 20√3/√3

= 20

Distance of the point O from the pole CD

OC = BC - BO

= 80 - 20

= 60

The height of the poles is 20√3 m and the distance of the point from the poles is 20 m and 60 m.

33.  A man sitting at a height of 20m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30° respectively. Find the width of the river. 

Solution

Height of tree AB = 20 m 
Angle of depression of pole 1 feet α = 60°
Angle of depression of pole 2 feet β = 30°
B₁C₁ be one pole and B₁C₂ be other sides width of river = B₁B₂
= B₁B + BB₂
The above information is G represent in from of figure as shown
In right triangle, if one of included angle is 0
tan θ = Opposite side/Adjacent side

34. A vertical tower stands on a horizontal plane and is surmounted by a flag - staff of height 7m. From a point on the plane, the angle of elevation of the bottom of the flag - staff is 30° and that of the top of the flag - staff is 45° . Find the height of the tower. 

Solution

Given 
Height of flagstaff  = 7m = BC 
Let height of tower = 'h'm = AB 
Angle of elevation of bottom of flagstaff α = 30°
Angle of elevation of top of flagstaff β = 45° 
Points of desecration be 'p' 
The above data is represented in form of figure as shown 
In right angle triangle if one of the induced angle is θ then 

tanθ = Opposite side/Adjacent side

35. The length of the shadow of a tower standing on level plane is found to be 2x metres longer when the sun's altitude is 30° than when it was 45°. Prove that the height of tower is x(√3 + 1) metres. 

Solution

Let, 
Length of shadow be 'a' m [BC] when sun attitude be = 45°
Length of shadow will be (2x + a)m = 80 when sun attitude is β = 30°

Let height of tower be 'h' m = AB the above information is represented in form of figure as shown 

In right triangle one of the included angle is θ then 
tan θ = Opposite side/Adjacent side 

In ABC 

36. A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 meters. Find the height of the tree. 

Solution

Let AB be height of tree it is broken at pointe and top touches ground at B' 
Angle made by top α = 30° 
Distance from foot of tree from point where A touches ground = O meter 
The above information is represented in form of figure as shown 
Height of tree = AB = AC + CB 
= AC + CB'
In right triangle If one of angle is θ then 

tanθ = Adjacent side/Opposite side 
cosθ = Adjacent side/Hypotenuse 

37. A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable. 

Solution

Length of cable connected to balloon = 215m[CB]
Angle of inclination of cable with ground α = 60° 
Height of balloon from ground = 'h'm = AB 
The above data is represented in form of figure as shown 
In right triangle one of the included angle is θ then 
sin θ = Opposite side/hypotenuse 

38. Two men on either side of the cliff 80 m high observes the angles of elevation of the top of the cliff to be 300 and 600 respectively. Find the distance between the two men. 

Solution 

Height of cliff = 80m = AB.

39. Find the angle of elevation of the sun (sun's altitude) when the length of the shadow of a vertical pole is equal to its height. 

Solution

Let 
Height of pole = 'h'm = sun's altitude from ground length of shadow be 'l' 
Given that l = h 
Angle of elevation of sun's altitude be θ the above data is represented in form of figure as shown 

In right triangle if one of the included angle is 0 then. 

tan θ = Opposite side/Adjacent side 

40. A fire in a building B is reported on telephone to two fire stations P and 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel ? 

Solution

Let AB be the building 
Angle of elevation from point P [ Fire station l]α = 60°

Angle of elevation from point Q [ Fire station l] β = 45°
Distance between fire stations PQ = 20 km 
The above information is represented in form of figure as shown 
In right triangle if one of the angle is θ then. 

tan θ = Opposite side/Adjacent side 

41. A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff. 

Solution 

Height of ship from water level = 10 cm = AB 
Angle of elevation of top of cliff α = 45°

Angle of depression of bottom of cliff α = 30°

Height of cliff CD = 'h'm. 

Distance of ship from foot of tower cliff 
Height of cliff above ship be 'a' m 
Then height of cliff = DX + XC = (10 + 0) m 
The above data is represented in form of figure as shown 
In right triangle, if one of the included angle is θ, then  
tan θ = Opposite side/Adjacent side 

42. A man standing on the deck of a ship, which is 8 m above water level. He observes the  angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30° . Calculate the distance of the hill from the ship and the height of the hill.

Solution

Height of ship above water level = 8m = AB 
Angle of elevation of top of cliff (hill) α = 60° 
Angle of depression of bottom of hill β = 30° 
Height of hill = CD 
Distance between ship and hill = AX . 
Height of hill above ship  = CX = 'a', 
Height of hill = (a + 8)m. 

The above data is represented in form of figure as shown  
In right triangle if one of included angle is θ then 
tan θ = Opposite side/Adjacent side 

43. There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple. 

Solution

Height of temple l (AB) = 50 m 
Angle of depression of top of temple 2, α = 30° 
Angle of depression of bottom of temple 2, β = 60° 

Height of temple 2 (CD) = 'h'm 
Width of river = BD = 'x'm. the above data is represents in form of figure as shown 

In right triangle if one of 'h' m included angle is θ, then 
tan θ = Opposite side/Adjacent side 
here BD = CX, CD = BX, 

Width of river = 50/√2 m 
Height of temple 2 = 100/3 m 

44. The angle of elevation of an aeroplane from a point on the ground is 45° . After a flight of 15 seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 3000 meters, find the speed of the aeroplane. 

Solution

Let aeroplane travelled from A to B in 15 sec 
Angle of elevation of point A  α = 45° 

Angle of elevation of point B β = 30° 
Height of aeroplane from ground = 3000 meters = AP = BQ 
Distance travelled in 15 sees = AB = PQ 
Velocity (or) speed = distance travelled time the above data is represents is form of figure as shown 
In right triangle one of the included angle is θ then 
tan θ = Opposite side/Adjacent side 

45. An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30° . Find the speed of the aeroplane in km/hr. 

Solution

Let aeroplane travelled from A to B in 10 secs 
Angle of elevation of point A = α = 60°
Angle of elevation of point B = β = 30° 
Height of aeroplane from ground = 1 km = AP = BQ 
Distance travelled in 10 sec = Ab = PQ 
The above data is represent in form of figure as shown 
In right triangle is one of the included angle is θ then 
tan θ = Opposite side/Adjacent side 

46. From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole. 

Solution

AB = height of tower = 50m. 
CD = height of (Pole) 
Angle of depression of top of building α = 45°

Angle of depression of bottom of building β = 60° 
The above data is represent in the form of figure as shown 
In right triangle one of included angle is θ then  
tan θ = Opposite side/Adjacent side 

47.  The horizontal distance between two trees of different heights is 60 m. The angle of  depression of the top of the first tree when seen from the top of the second tree is 45° . If the height of the second tree is  80 m, find the height of the first tree. 

Solution

Distance between trees = 60m. [80]
Height of second tree = 80m [CD] 
Let height of first tree = 'h' m[AB]
Angle of depression from second tree top from first tree top α = 45°

The above information is represent in form of figure as shown 
In right triangle if one of the included angle is 0 their 
tan θ = Opposite side/Adjacent side 

= 80 - 60 = 20 m 
Height of second tree = 80 m 
Height of first tree = 20 m 

48. A tree standing on a horizontal plane is learning towards east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β Prove that the height of the top from the ground is [(b -a ) tan α tan β]/(tan α tan β).

Solution

AB be the tree leaning east 

From distance 'a' m from tree, Angle of elevation be α at point P. 

From distance 'b' m from tree, Angle of elevation be β at point Q. 
The above data is represented in the form of figure as shown in right triangle if one of the included angle is θ then 
tan θ = Opposite side/Adjacent side 

49. The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45° . 

Calculate the height of the tower.

Solution

50. The angle of elevation of a stationery cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45° . What is the height of the cloud above the lake level ? (Use tan 15° = 0.268)

Solution

Let cloud be at height PQ as represented from lake level 
From point x, 2500 meters above the lake angle of elevation of top of cloud α = 15°

Angle of depression of shadow reflection in water β = 45°

Here PQ = PQ' draw AY ⊥ PQ 
Let AQ = 'h' mAP = 'x' m. 

PQ = (h + x)m PQ' = (h + x)m 
The above data is represented in from of figure as shown 
In right triangle if one of included angle is θ then 
tan θ = Opposite side/Adjacent side 

tan 15° = AQ/AY 

51. If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is (2 h sec α)/(tanβ - tan α)

Solution

Let x be point 'b' meters above lake 
Angle of elevation of cloud from X = α
Angle of depression of cloud refection in lake = β 
Height of cloud from lake = PQ 
PQ' be the reflection then = PQ' = PQ 
Draw XA ⊥ PQ, AQ = 'x' m 
AP = XY = 'h'm . 
Distance of cloud from point of observation is XQ 

The above data is represented in form of figure as shown 

52. From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be α  and β. Show that the height in miles of aeroplane above the road is given by (tan α tan β)/(tan α + tan β) 

Solution

Let PQ be height of aeroplane from ground x and y be two mile stones on opposite sides of the aeroplane xy = 1 mile 
Angle of depression of x from p = α 
Angle of depression of y from p = β
The above data is represented in form of figure as shown 

In right triangle, if one of included angle is θ then 

tan θ = Opposite side/Adjacent side 

53. PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post. 

Solution

PQ is part height = 'a' m AB is tower height 

Angle of elevation of B from P = α 
Angle of elevation of B from Q = β 
The above information is represented in form of figure as shown 
In right triangle if one of the included angle is θ, then 
tan θ = Opposite side/Adjacent side 

54. A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal. 

Show that a/b = (cos α - cos β)/(sin β - sin α)

Solution

Let AB be ladder initially at an inclination α to ground 

When its foot is pulled through distance 'a' let BB' = 'a' m and AA' = 'b' m 

New angle of elevation from B' = B the above information is represented in form of figure as shown 

55. A tower subtends an angle α at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β . Prove that the height of the tower is b tan α cot β. 

Solution

Let height of tower be 'h' m = PQ 
Angle of elevation at point A on ground = α
Let B be point 'b' m above the A. 

Angle of depression of foot of tower from B = β the above data is represented in from of figure as shown draw BX ⊥ PQ from figure QX = 'b' m  
In  ΔPBX 

56. An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye. 

Solution

Height of observer = AB = 1.5 m 
Height of tower = PQ = 30 m 
Height of tower above the observe eye = 30 - 1.5
QX = 28.5 m . 

Distance between tower and observe XB = 28. 5 m . 
θ be angle of elevation of tower top from eye 
The above data is represented in from of figure as shown from figure 

tan θ = Opposite side/Adjacent side 

tan θ = QX/BX  = 28.5/28.5 = 1

⇒ θ = tan^–1 (1) = 45°

Angle of elevation = 45°

57. A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances. 

Solution

Let AB be height of stool  = 1.5m 
Let P and Q be equal distance then AP= 0.5m, AQ = 1 m the above information is represented in form of figure as shown 
BC = Length of leg 

58. A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30° . Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45° . Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet. 

Solution

For boy 
Length of string AB = 100 m. 
Angle Made by string with ground = α = 30°

For boy 2 
Height of building CD = 10 m. 

Angle made by string with building top β = 45° length of kite thread of boy 2 of both the kites meet must be 'DB'
The above information is represented in form of figure as shown 

59. The angle of elevation of the top of a hill at the foot of a tower is  60° and the angle of elevation of the top of the tower from the foot of the hill is 30° . If the tower is 50 m high, what is the height of the hill ? 

Solution

Height of towers AB = 50 m 
Height of hill CD = 'h' m.
Angle of elevation of top of hill from of tower α = 60° . 

Angle of elevation of top of tower from foot of hill β = 30° . 

The above information is represented I form of figure as shown 
From figure 

In ΔABC,

60. Two boats approach a light house in mid - sea from opposite directions. The angles of elevation of the top of the light house from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the light house. 

Solution

61. From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find 

(i) The horizontal distance between AB and CD. 

(ii) The  height of the lamp post. 

(iii) The difference between the heights of the building and the lamp post. 

Solution

Height of building AB = 60 m. 

Height of lamp post CD = h m

Angle of depression of top of lamp post from top of building α = 30°

Angle of depression of bottom of lamp post from top of building β = 60°

The above information is represented in the form of figure as shown 

62. From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the light house be h meters and the line joining the ships passes through the foot of the light house, show that the distance  h(tan α + tan β)/(tan α tan β) metres.

Solution

Height of light house = 'h' meters = AB

63. A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance between the two cars and how far is each car from the tower ? 

Solution

Height of towers AB = 50 m 

64. The angles of elevation of the top of a rock from the top and foot of a loo m high tower are respectively 30° and 45° . Find the height of the rock. 

Solution

Height of tour AB = 100 m 
Height of rock CD = 'h' m 
Angle of elevation of top of root from top of tower α = 30°

Angle of elevation of top of root from bottom of tower β = 45°

The above data is represented in form of figure as shown 

65. As observed from the top of a 150 m tall light house, the angles of depression of two ships approaching it are 30° and 45° . If one ship is directly behind the other, find the distance between the two ships 

Solution

Height of light house AB = 150 m

66. A flag - staff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flag - staff is 60° and from the same point, the angle of elevation of the top of the flag - staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flag-staff. 

Solution

Height of tower = AB = 5 m. 
Height of flagstaff BC = 'h' m
Angle of elevation of top of flagstaff α = 60° 
Angle of elevation of bottom of flagstaff β = 45°

The above data is represented in form of figure as shown 

67. The angles of elevation of the top of a tower from two point at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.

Solution

Height of tower AB = 'h' meters 

Let point C be 4 meters from B, Angle of elevation be α given point D be 9 meters from B. 

Angle of elevation be β. given α , β are complementary, α + β = 90° ⇒ β = 90° - α
required to prove that h = 6 meters 

The above data is represented in the form of figure as shown 

∴ height of tower = 6 meters. 

68. The angles of depression of two ships from the top of a light house and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the light house. 

Solution

Height of light house AB = 'h' meters