RD Sharma Solutions Chapter 11 Constructions Exercise 11.3 Class 10 Maths

Chapter Name | RD Sharma Chapter 11 Constructions |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 11.3 Solutions
1. Construct a ΔABC in which BC = 3.6 cm, AB + AC = 4.8 cm and ∠B= 60° .
Solution
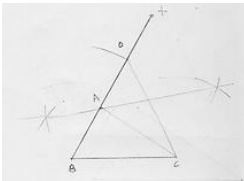
Steps of construction:
1. Draw a line segment BC of 3.6 cm.
2. At the point B, draw ∠x BC of 60°
3. With center B and radius 4.8 cm, draw an arc which intersects XB at D.
4. Join DC
5. Draw the perpendicular bisector of DC which intersects DB at A.
6. Join AC
Hence, ΔABC is the required triangle
2. Construct a ΔABC in which AB + AC = 5.6 cm, BC = 4.5 cm, AB - AC = 1.5 cm and ∠B = 45° .
Solution

3. Construct a ΔABC in which BC = 3.4 cm, AB - AC = 1.5 cm and ∠B = 45°
Solution

Steps of construction:
Step 1: Draw a line segment BC of 3.5cm.
Step 2: At B, draw an angle XBC of 45°
Step 3: With center B and radius 1.5 cm, draw an arc which intersects BX at D.
Step 4: Join DC
Step 5: Draw the perpendicular bisector of DC which intersects BD produced at A.
Step 6: Join AC
∴ ΔABC is the required triangle
4. Using ruler and compasses only, construct a ΔABC, given base BC = 7 cm, ∠ABC = 60° and AB + AC = 12 cm.
Solution

Steps of construction:
1. Draw a line segment BC of 7 cm.
2. At B, draw an angle XBC of 60°
3. With center B and radius 12 cm, draw an arc which intersects BX at D.
4. Join DC
5. Draw the perpendicular bisector of DC which intersects BD at A.
6. Join AC
∴ Δ ABC is the required triangle.
5. Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45° .
Solution

1. Draw a line segment XY of 6.4 cm.
2. Draw a ∠DXY = B = 60° and ∠EYX = ∠C = 45°
3. Draw the angle bisector of ∠DXY and ∠EYX which interest each other at A.
4. Draw the perpendicular bisector of AX and AY which interest XY at B and C respectively.
5. Join AB and AC
∴ Δ ABC is the required triangle.
∴ Δ ABC is the required triangle.
6. Using ruler and compasses only, construct a ΔABC from the following data:
AB + BC+ CA = 12 cm, ∠B = 45° and ∠C = 60° .
AB + BC+ CA = 12 cm, ∠B = 45° and ∠C = 60° .
Solution

Steps of construction :
Step 1: Draw a line segment XY of 12 cm.
Step 2: Draw ∠DXY = ∠B = 45° and ∠EYX = ∠C = 60°
Step 3: Draw the angle bisectors of angles of DXY and EYX which intersects each other at A. Step 2: Draw ∠DXY = ∠B = 45° and ∠EYX = ∠C = 60°
Step 4: Draw the pependicular of AX and AY which intersect XY at B and C respectively.
Step 5: Join AB and AC
∴ Δ ABC is the required triangle.


9. Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Step 5: Join AB and AC
∴ Δ ABC is the required triangle.
7. Construct a right - angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60° .
Solution

Steps of construction :
Step 1: Draw a line segment XY of 10 cm.
Step 2: Draw ∠DXY = ∠B = 90° and ∠FYX = ∠C = 60°
Step 3: Draw the angle bisectors of ∠DXY and ∠EYX which intersects each other at A.
Step 3: Draw the angle bisectors of ∠DXY and ∠EYX which intersects each other at A.
Step 4: Draw the perpendicular of AX and AY which intersect XY at B and C respectively.
Step 5: Join AB and AC
∴ Δ ABC is the required triangle.
8. Construct a triangle ABC such that BC = 6 cm, AB = 6cm and median AD = 4 cm.
Solution

Steps of Construction :
Step 1 : Draw a line segment BC of 6 cm.
Step 2 : Take midpoint D of BC.
Step 3 : with center B and D and radii 6 cm and 4 cm draw two arcs which intersects each other A.
Step 4 : Join AB, AD and AC
∴ Δ ABC is the required triangle.
Solution

Step 1: Draw a line segment BC of 6 cm.
Step 2: At B draw an angle le × BC of 90° .
Step 3: with center B and radius 10 cm draw an arc which intersects XB at D.
Step 4: Join DC.
Step 5: Draw the perpendicular bisector of DC which intersects DB at A.
Step 6: Join AC

∴ Δ ABC is the required triangle.
10. Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11.
Solution

Steps of construction :
Step 1: Draw a line segment AB of 11 cm.
Step 2: Draw ∠DAB = Y = 30° and ∠FBA = ∠Z = 90°
Step 3: Draw the angle bisector of ∠DAB and ∠EBA which intersect each other at x Step 4: Draw the perpendicular bisector XA and XB which intersect AB at Y and Z respectively.
Step 5: Join XY and XZ
∴ Δ XYZ is the required triangle.
