RS Aggarwal Solutions Chapter 16 Coordinate Geometry Exercise 16B Class 10 Maths

Chapter Name | RS Aggarwal Chapter 16 Coordinate Geometry |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 16B Solutions
1. Find the coordinates of the point which divides the join of A(-1. 7) and B(4, -3) in the ratio 2 : 3
Solution
The end points of AB are A(-1, 7) and B(4, -3)
Therefore (x1 = -1, y1 = 7) and (x2 = 4, y2 = -3)
Also, m = 2 and n = 3
Let the required point be P(x, y)
By section formula, we get
x = (mx2 + nx1)/(m + n), y = (my2 + ny1)/(m + n)
⇒ x = {2 × 4 + 3 × (-1)}/(2 + 3), y = {2 × (-3) + 3 × 7}/(2 + 3)
⇒ x = (8 – 3)/5, y = (-6 + 21)/5
⇒ x = 5/5, y = 15/5
Therefore, x = 1 and y = 3
Hence, the coordinates of the required point are (1, 3).
2. Find the co-ordinates of the point which divides the join of A(-5, 11) and B(4, -7) in the ratio 7: 2.
Solution
The end points of AB are A(-5, 11) and B(4, -7)
Therefore, (x1 = - 5, y1 = 11) and (x2 = 4, y2 = -7)
Also, m = 7 and n = 2
Let the required point be P(x, y).
By section formula, we get
x = (mx2 + nx1)/(m + n), y = (my2 + ny1)/(m + n)
⇒ x = {7 × 4 + 2 × (-5)}/(7 + 2), y = {7 × (-7) + 2 × 11}/(7 + 2)
⇒ x = (28 – 10)/9, y = (-49 + 22)/9
⇒ x = 18/9, y = -(27/9)
Therefore, x = 2 and y = - 3
Hence, the required point are P(2, -3).
3. If the coordinates of points A and B are (-2, -2) and (2, -4) respectively. Find the coordinates of the point P such that AP = 3/7 AB, where P lies on the segment AB.
Solution
The coordinates of the points A and B are (-2, -2) and (2, -4) respectively, where
AP = 3/7 AB and P lies on the line segment AB. So
AP + BP = AB
⇒ AP + BP = 7AP/3 (∵ AP = 3/7 AB)
⇒ BP = 7AP/3 – AP
⇒ AP/BP = 3/4
Let (x, y) be the coordinates of P which divides AB in the ratio 3 : 4 internally. Then
x = {(3 × 2 + 4 × (-2)}/(3 + 4) = (6 – 8)/7 = -(2/7)
y = {3 × (-4) + 4 × (-2)}/(3 + 4) = (-12 – 18)/7 = -(20/7)
Hence, the coordinates of point P are (- 2/7, - 20/7).
4. Point A lies on the line segment PQ joining P(6, -6) and Q(-4, 1) in such a way that PA/PQ = 2/5. If that point A also lies on the line 3x + k(y + 1) = 0 find the value of k.
Solution
Let the coordinates of A be (x, y). Here PA/PQ = 2/5 so,
PA + AQ = PQ
⇒ PA + AQ = 5PA/2 [∵ PA = 2/5 PQ)
⇒ AQ = 5PA/2 – PA
⇒ AQ/PA = 3/2
⇒ PA/AQ = 2/3
Let (x, y) be the coordinates of A, which dives PQ in the ratio 2 : 3 internally, Then using section formula, we get
x = {(2 × (-4) + 3 × (6)}/(2 + 3) = ( -8 + 18)/5 = 10/5 = 2
y = {2 × (-1) + 3 × (-6)}/(2 + 3) = (-2 -18)/5 = -20/5 = - 4
Now, the point (2, -4) lies on the line 3x + k(y + 1) = 0, therefore
3 × 2 + k (-4 + 1) = 0
⇒ 3k = 6
⇒ k = 6/3 = 2
Hence, k = 2.
5. Points P, Q, R and S divide the line segment joining the points A(1, 2) and B(6, 7) in five equal parts. Find the coordinates of the points P, Q and R.
Solution
Since, the points P, Q, R and S divide the line segment joining the points A(1, 2) and B(6, 7) in five equal parts, so
AP = PQ = QR = R = SB
Here, point P divides AB in the ratio of 1 : 4 internally. So using section formula, we get
Coordinates of P = {(1 × (6) + 4 × (1)}/(1 + 4), {(1 × (7) + 4 × (2)}/(1 + 4)
= (6 + 4)/5, (7 + 8)/5
= (2, 3)
The point Q divides AB in the ratio of 2 : 3 internally. So using section formula, we get
Coordinates of Q = {(2 × (6) + 3 × (1)}/(2 + 3), {(2 × (7) + 3 × (2)}/(2 + 3)
= (12 + 3)/5, (14 + 6)/5
= (3, 4)
The point R divides AB in the ratio of 3 : 2 internally So using section formula, we get
Coordinates of R = (3 × (6) + 2 × (1)/(3 + 2) , (3 × (7) + 2 × (2)}/(3 + 2)
= (18 + 2)/5, (21 + 4)/5
= (4, 5)
Hence, the coordinates of the points P, Q and R are (2, 3), (3, 4) and (4, 5) respectively.
6. Points P, Q and R in that order are dividing line segment joining A(1, 6) and B(5, -2) in four equal parts. Find the coordinates of P, Q and R.
Solution
The given points are A(1, 6) and B(5, -2)
Then P(x, y) is a point that devices the line AB in the ratio 1 : 3
By the section formula:
x = (mx2 + nx1)/(m + n), y = (my1 + ny1)/(m + n)
⇒ x = (1 × 5 + 3 × 1)/(1 + 3), y = (1 × (-2) + 3 × 6)/(1 + 3)
⇒ x = (5 + 3)/4, y = (-2 + 18)/4
⇒ x = 8/4, y = 16/4
⇒ x = 2 and y = 4
Therefore, the coordinates of point P are (2, 4)
Let Q be the mid-point of AB
Then, Q (x, y)
x = (x1 + x2)/2, y = (y1 + y2)/2
⇒ x = (1 + 5)/2, y = (6 + (-2)/2
⇒ x = 6/2, y = 4/2
⇒ x = 3, y = 2
Therefore, the coordinates of Q are (3, 2)
Let R(x, y) be a point that divides AB in the ratio 3 : 1
Then, by the section formula:
x = (mx2 + nx1)/(m + n) , y = (my2 + ny1)/(m + n)
⇒ x = (3 × 5 + 1 × 1)/(3 + 1), y = (3 × (-2) + 1 × 6)/(3 + 1)
⇒ x = (15 + 1)/4, y = (3 × (-2) + 1 × 6)/(3 + 2)
⇒ x = (15 + 1)/4, y = (-6 + 6)/4
⇒ x = 16/4, y = 0/4
⇒ x = 4 and y = 0
Therefore, the coordinates of R are (4, 0).
Hence, the coordinates of point P,Q and Rare (2, 4), (3, 2) and (4, 0) respectively.
7. The line segment joining the points A(3, -4) and B(1, 2) is trisected at the points P(p, -2) and Q(5/3, q). Find the values of p and q.
Solution
Let P and Q b the points of trisection of AB
Then P divides AB in the ratio 1 : 2
So, the coordinates of P are
x = (mx2 + nx1)/(m + n), y = (my2 + ny1)/(m + n)
⇒ x = (1 × 1 + 2 × (3)}/(1 + 2), y = {1 × 2 + 2 × (-4)}/(1 + 2)
⇒ x = (1 + 6)/3, y = (2 – 8)/3
⇒ x = 7/3, y = -(6/3)
⇒ x = 7/3, y = -2
Hence, the coordinates of Pare (7/3, -2)
But, (p, -2) are the coordinates of P.
So, p = 7/3
Also, Q divides the line AB in the ratio 2 : 1
So, the coordinates of Q are
x = (mx2 + mx1)/(m + n), y = (my2 + my1)/(m + n)
⇒ x = (2 × 1 + 1 × 3)/(2 + 1), y = {2 × 2 + 1 × (-4)}/(2 + 1)
⇒ x = (2 + 3)/3, y = (4 – 4)/3
⇒ x = 5/3, y = 0
Hence, Coordinates of Q are (5/3, 0)
But the given coordinates of Q are (5/3, q)
So, q = 0
Thus, p = 7/3 and q = 0
8. Find the coordinates of the midpoints of the line segment joining
(i) A(3, 0) and B(-5, 4)
(ii) P(-11, -8) and Q(8, -2)
Solution
(i) The given points are A(3, 0) and B(-5, 4)
Let (x, y) be the midpoint of AB. Then:
x = (x1 + x2)/2, y = (y1 + y2)/2
⇒ x = {3 + (-5)}/2, y = (0 + 4)/2
⇒ x = -2/2, y = 4/2
⇒ x = -1, y = 2
Therefore, (-1, 2) are the coordinates of midpoint of AB.
(ii) The given points are P(-11, -8) and Q(8, -2).
Let (x, y) be the midpoint of PQ. Then:
x = (x1 + x2)/2, y = (y1 + y2)/2
x = (-11 + 8)/2, y = (-8 – 2)/2
⇒ x = - (3/2), y = -(10/2)
⇒ x = -(3/2), y = - 5
Therefore, (-3/2, - 5) are the coordinates of midpoint of PQ.
9. If (2, p) is the midpoint of the line segment joining the points A(6, - 5) and B(-2, 11) find the value of p.
Solution
The given points are A(6, - 5) and B(-2, 11)
Let (x, y) be the midpoint of AB. Then,
x = (x1 + x2)/2, y = (y1 + y2)/2
⇒ x = 6 + (-2)/2, y = (-5 + 11)/2
⇒ x = (6 – 2)/2, y = (- 5 + 11)/2
⇒ x = 4/2, y = 6/2
⇒ x = 2, y = 3
So, the midpoint of AB is (2, 3).
But it is given that midpoint of AB is (2, p).
Therefore, the value of p = 3
10. The midpoint of the line segment joining A(2a, 4) and B(-2, 3b) is C(1, 2a + 1). Find the values of and b.
Solution
The points are A(2a, 4) and B(-2, 3b)
Let C(1, 2a + 1) be the mid-point of AB. Then:
x = (x1 + x2)/2, y = (y1 + y2)/2
⇒ 1 = (2a (-2)/2, 2a + 1 = (4 + 3b)/2
⇒ 2 = 2a – 2, 4a + 2 = 4 + 3b
⇒ 2a = 2 + 2, 4a – 3b = 4 – 2
⇒ a = 4/2, 4a – 3b = 2
⇒ a = 2, 4a – 3b = 2
Putting the value of a in the equation 4a + 3b = 2, we get:
4(2) – 3b = 2
⇒ - 3b = 2 – 8 = - 6
⇒ b = 6/3 = 2
Therefore, a = 2 and b = 2
11. The line segment joining A(-2, 9) and B(6, 3) is a diameter of a circle with center C. Find the coordinates of C.
Solution
The given point are A(-2, 9) and B(6, 3)
Then, C(x, y) is the midpoint of AB.
x = (x1 + x2)/2, y = (y1 + y2)/2
⇒ x = (-2 + 6)/2, y = (9 + 3)/2
⇒ x = 4/2, y = 12/2
⇒ x = 2, y = 6
Therefore, the coordinates of point C are (2, 6).
12. Find the coordinates of a point A, where AB is a diameter of a circle with center C(2, -3) and the other end of the diameter is B (1, 4).
Solution
C(2, -3) is the center of the given circle. Let A(a, b) and B(1, 4) be the two end-points of the given diameter AB. Then, the coordinates of C are
x = (a + 1)/2, y = (b + 4)/2
It is given that x = 2 and y = - 3
⇒ 2 = (a + 1)/2, - 3 = (b + 4)/2
⇒ 4 = a + 1, - 6 = b + 4
⇒ a = 4 – 1, b = - 6 – 4
⇒ a = 3, b = - 10
Therefore, the coordinates of point A are (3, -10).
13. In what ratio does the point P(2, 5) divide the join of A (8, 2) and B(- 6, 9) ?
Solution
Let the point P(2, 5) divides AB in the ratio k : 1.
Then, by section formula, the coordinates of P are x = (-6k + 8)/(k + 1), y = (9k + 2)/(k + 1)
It is given that the coordinates of P are (2, 5)
⇒ 2 = (-6k + 8)/(k + 1), 5 = (9k + 2)/(k + 1)
⇒ 2k + 2 = -6k + 8, 5k + 5 = 9k + 2
⇒ 2k + 6k = 8 – 2, 5 – 2 = 9k – 5k
⇒ 8k = 6, 4k = 3
⇒ k = 6/8, k = 3/4
⇒ k = 3/4 in each case.
Therefore, the point P(2, 5) divides AB in the ratio 3 : 4.
14. Find the ratio in which the point P(3/4, 5/12) divides the line segment joining the points A(1/2, 3/2) and B(2, -5).
Solution
Let k : 1 be the ratio in which the point P(3/4, 5/12) divides the line segment joining the points A(1/2, 3/2) and (2, -5). Then
(3/4, 5/12) = {k(2) + 1/2/(k + 1), k(-5) + 2/2)/(k + 1)}
⇒ {k(2) + 1/2}/(k + 1) = 3/4 and {k(-5) + 3/2}/(k + 1) = 5/12
⇒ 8k + 2 = 3k + 3 and – 60k + 18 = 5k + 5
⇒ k = 1/5 and k = 1/5
Hence, required ratio is 1 : 5.
15. Find the ratio in which the point P(m, 6) divides the join of A(-4, 3) and B(2, 8). Also, find the value of m.
Solution
Let the point P(m, 6) divide the line AB in the ratio k : 1.
Then, by the section formula:
x = (mx2 + nx1)/(m + n), y = (my2 + ny1)/(m + n)
The coordinates of P are (m, 6).
m = (2k – 4)/(k + 1), 6 = (8k + 3)/(k + 1)
⇒ m(k + 1) = 2k – 4, 6k + 6 = 8k + 3
⇒ m(k + 1) = 2k – 4, 6 – 3 = 8k – 6k
⇒ m(k + 1)= 2k – 4, 2k = 3
⇒ m(k + 1) = 2k – 4, k = 3/2
Therefore, the point P divides the line AB in the ratio 3 : 2.
Now, putting the value of k in the equation m(k + 1) = 2k – 4, we get:
m(3/2 + 1) = 2(3/2) – 4
⇒ m (3 + 2)/2 = 3 – 4
⇒ 5m/2 = - 1
⇒ 5m = -2
⇒ m = -(2/5)
Therefore, the value of m = -(2/5)
So, the coordinates of P are (-2/5, 6).
16. Find the ratio in which the print (-3, k) divide the join of A(-5, -4) and B(-2, 3). Also, find the value of k.
Solution
Let the point P(-3, k) divide the line AB in the ratio s : 1
Then, by the section formula:
x = (mx1 + nx1)/(m + n), y = (my2 + ny1)/(m + n)
The coordinates of P are (-3, k).
-3 = (-2s – 5)/(s + 1) , k = (3s – 4)/(s + 1)
⇒ - 3s – 3 = - 2s – 5, k(s + 1) = 3s – 4
⇒ - 3s + 2s = - 5 + 3, k(s + 1) = 3s – 4
⇒ - s = - 2, k(s + 1) = 3s – 4
⇒ s = 2, k(s + 1) = 3s – 4
Therefore, the point P divides the line AB in the ratio 2 : 1.
Now, Putting the value of s in the equation k(s + 1) = 3s – 4, we get:
k(2 + 1) = 3(2) – 4
⇒ 3k = 6 – 4
⇒ 3k = 2
⇒ k = 2/3
Therefore, the value of k = 2/3
That is, the coordinates of P are (-3, 2/3).
17. In what ratio is the line segment joining A(2, -3) and B(5, 6) divide by the x-axis ? Also, find the coordinates of the point of division.
Solution
Let AB be divided by the x-axis in the ratio k : 1 at the point P.
Then, by section formula the coordinates of P are
P = (5k + 2)/(k + 1), (6k – 3)/(k + 1)
But P lies on the x-axis, so, its ordinate is 0.
Therefore, (6k – 3)/|(k + 1) = 0
⇒ 6k – 3 = 0
⇒ 6k = 3
⇒ k = 3/6
⇒ k = 1/2
Therefore, the required ratio is 1/2 : 1, which is same as 1 : 2.
Thus, the x-axis divides the line AB lie in the ratio 1 : 2 at the point P.
Applying k = 1/2, we get the coordinates of point,

Hence, the point of intersection of AB and the x-axis is P(3, 0)
18. In what ratio is the line segment joining the points A(-2, -3) and B(3, 7) divided by the y-axis? Also, find the coordinates of the point of division.
Solution
Let AB be divided by the x-axis in the ratio k : 1 at the point P.
Then, by section formula the coordinates of P are
P = {(3k – 2)/(k + 1), (7k – 3)/(k + 1)}
But P lies on the y-axis; so, its abscissa is 0.
Therefore, the required ratio is 2/3 : 1, which is same as 2 : 3
Thus, the x-axis divides the line AB in the ratio 2 : 3 at the point P.
Applying k = 2/3, we get the coordinates of point

Hence, the point of intersection of AB and the x-axis is P(0, 1).
19. In what ratio does the line x – y – 2 = 0 divide the line segment joining the points A(3, -1) and B(8, 9) ?
Solution
Let the line x – y – 2 = 0 divide the line segment joining the points A(3, -1) and B(8, 9) in the ratio k : 1 at P.
Then, the coordinates of P are
P(8k + 3)/(k + 1), (9k – 1)/(k + 1)
Since, P lies on the line x – y – 2 = 0, we have:
(8k + 3)/(k + 1) – (9k – 1)/(k + 1) – 2 = 0
⇒ 8k + 3 – 9k + 1 – 2k – 2 = 0
⇒ 8k – 9k – 2k + 3 + 1 – 2 = 0
⇒ - 3k + 2 = 0
⇒ -3k = -2
⇒ k = 2/3
So, the required ratio is 2/3 : 1, which is equal to 2 : 3.
20. Find the lengths of the medians of a △ABC whose vertices are A(0, -1), B(2, 1) and C(0, 3).
Solution
The vertices of △ABC are A(0, -1), B(2, 1) and C(0, 3).
Let AD, BE and CF be the medians of △ABC.

Let D be the midpoint of BC. So, the coordinates of D are
D(2 + 0)/2, (1 + 3)/2 i.e., D(2/2, 4/2) i.e., D(1, 2)
Let E be the midpoint of AC. So the coordinate of E are
E(0 + 0)/2, (-1 + 3)/2 i.e., E(0/2, 0/2) i.e, E(0, 1)
Let F be the midpoint of AB. So the coordinates of F are
F(0 + 2)/2, (- 1 + 1)/2 i.e., F(2/2, 0/2) i.e., F(1, 0)

21. Find the centroid of △ABC whose vertices are A(-1, 0), B(5, -2) and C (8, 2)
Solution
Here, (x1 = -1, y1 = 0), (x2 = 5, y2 = -2) and (x3 = 8, y3 = 2)
Let G (x, y) be the centroid of the △ABC. Then,
x = 1/3(x1 + x2 + x3) = 1/3(-1 + 5 + 8) = 1/3(12) = 4
y = 1/3(y1 + y2 + y3) = 1/3(0 – 2 + 2) = 1/3(0) = 0
Hence, the centroid of △ABC is G(4, 0).
22. If G(-2, 1) is the centroid of a △ABC and two of its vertices are A(1, -6) and B(-5, 2), find the third vertex of the triangle.
Solution
Two vertices of △ABC are A(1, -6) and B(-5, 2).
Let the third vertex be C(a, b).
Then, the coordinates of its centroid are
C(1 – 5 + a)/3, (-6 + 2 + b)/3)
C(-4 + a)/3, (-4 + b)/3
But it is given that G(-2, 1) is the centroid. Therefore,
-2 = (-4 + a)/3, 1 = (-4 + b)/3
⇒ 6 = - 4 + a, 3 = - 4 + b
⇒ - 6 + 4 = a, 3 + 4 = b
⇒ a = - 2, b = 7
Therefore, the third vertex of △ABC is C(-2, 7).
23. Find the third vertex of a △ABC if two of its vertices are B(-3, 1) and C(0, -2), and its centroid is at the origin.
Solution
Two vertices of △ABC are B(-3, 1) and C(0, -2). Let the third vertex be A(a, b).
Then, the coordinates of its centroid are
(-3 + 0 + a)/3, (1 – 2 + b)/2
i.e., (-3 + a)/3, (-1 + b)/3)
But it is given that centroid is at the origin, that is G(0, 0). Therefore,
0 = (-3 + a)/3, 0 = (-1 + b)/3
⇒ 0 = - 3 + a, 0 = -1 + b
⇒ 3 = a, 1 = b
⇒ a = 3, b = 1
Therefore, the third vertex of △ABC is A(3, 1).
24. Show that the points A(3, 1), B(0, -2), C(1, 1) and D(4, 4) are the vertices of parallelogram ABCD.
Solution
The points are A(3, 1), B(0, -2), C(1, 1) and D(4, 4)
Join AC and BD, intersecting at O.

We know that the diagonals of a parallelogram bisect each other.
Midpoint of AC = (3 + 1)/2, (1 + 1)/2 = (4/2, 2/2) = (2, 1)
Midpoint of BD = (0 + 4)/2, (-2 + 4)/2 = (4/2, 2/2) = (2, 1)
Thus, the diagonals AC and BD have the same midpoint
Therefore, ABCD is a parallelogram.
25. If the points P(a, -11) , Q(5, b), R(2, 15) and S(1, 1) are the vertices of a parallelogram PQRS, find the values of a and b.
Solution
The points are P(a, -11), Q(5, b), R(2, 15) and S(1, 1).
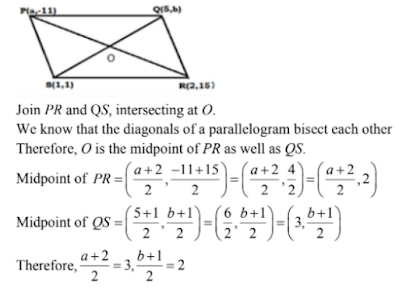
⇒ a + 2 = 6, b + 1 = 4
⇒ a = 6 – 2, b = 4 – 1
⇒ a = 4 and b = 3
26. If three consecutive vertices of a parallelogram ABCD are A(1, -2), B(3, 6) and C(5, 10). Find its fourth vertex D.
Solution
Let A(1, -2), B(3, 6) and C(5, 10) be the three vertices of a parallelogram ABCD and the fourth vertex be D(a, b).
Join AC and BD intersecting at O.

Therefore, O is the midpoint of AC as well as BD.
Midpoint of AC = (1 + 5)/2, (-2 + 10)/2 = (6/2, 8/2) = (3, 4)
Midpoint of BD = {(3 + a)/2, (6 + b)/2}
Therefore, (3 + a)/2 = 3 and (6 + b)/2 = 4
⇒ 3 + a = 6 and 6 + b = 8
⇒ a = 6 – 3 and b = 8 – 6
⇒ a = 3 and b = 2.
Therefore, the fourth vertex is D(3, 2).
27. In what ratio does y-axis divide the line segment joining the points (-4, 7) and (3 -7)?
Solution
Let y-axis divides the line segment joining the points (-4, 7) and (3, -7) in the ratio k : 1. Then
0 = (3k – 4)/(k + 1)
⇒ 3k = 4
⇒ k = 4/3
Hence, the required ratio is 4 : 3.
28. If the point P(1/2, y) lies on the line segment joining the points A(3, -5) and B(-7, 9) then find the ratio in which P divides AB. Also, find the value of y.
Solution
Let the point P(1/2, y) divides the line segment joining the points A(3, -5) and B(-7, 9) in the ratio k : 1. Then
(1/2, y) = {(k (-7) + 3)/(k + 1), {k(9) – 3)/(k + 1)}
⇒ (-7k + 3)/(k + 1) = 1/2 and (9k – 5)/(k + 1) = y
⇒ k + 1 = -14 k + 6
⇒ k = 1/3
Now, substituting k = 1/3 in (9k – 5)/(k + 1) = y, we get
(9/3 – 5)/(1/3 + 1) = y
⇒ y = (9 – 15)/(1 + 3) = -(3/2)
Hence, required ratio is 1 : 3 and y = -(3/2).
29. Find the ratio which the line segment joining the points A(3, -3) and B(-2, 7) is divided by x-axis. Also, find the point of division.
Solution
The line segment joining the points A(3, - 3) and B(-2, 7) is divided by x-axis. Let the required ratio be k : 1, So,
Now,

Hence, the required ratio is 3 : 7 and the point of division is (3/2, 0)
30. The base QR of an equilateral triangle PQR lies on x-axis. The coordinates of the point Q are (-4, 0) and origin is the midpoint of the base. Find the coordinates of the point P and R.
Solution
Let (x, 0) be the coordinates of R. Then
0 = (-4 + x)/2
⇒ x = 4
Thus, the coordinates of R are (4, 0).
Here PQ = QR = PR and the coordinates of P lies on y-axis. Let the coordinates of P be (0, y). Then,
PQ = QR
⇒ PQ2 = QR2
⇒ (0 + 4)2 + (y + 0)2 = 82
⇒ y2 = 64 – 16 = 48
⇒ y = ±4√3
Hence, the required coordinates are R(4, 0) and P(0, 4√3) or P(0, -4√3).
31. The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of point C are (0, -3). The origin is the midpoint of the base. Find the coordinates of the points A and B. Also, find the coordinates of another point D such that ABCD is a rhombus.
Solution
Let (0, y) be the coordinates of B. Then
0 = (-3 + y)/2
⇒ y = 3
Thus, the coordinates of B are (0, 3)
Here, AB = BC = AC and by symmetry the coordinates of A lies on x-axis.
Let the coordinates of A be (x, 0), Then
AB = BC
⇒ AB2 = BC2
⇒ (x – 0)2 + (0 – 3)2 = 62
⇒ x2 = 36 – 9 = 27
⇒ x = ±3√3
If the coordinates of point A are (3, √3, 0) then the coordinates of D are (-3√3, 0).
If the coordinates of point A are (-3√3, 0) then the coordinates of D are (-3√3, 0)
Hence, the required coordinates are A(3√3, 0), B(0, 3) and D(-3√3, 0) or A(3√3, 0) and D(-3√3, 0) or A(-3√3, 0), B(0, 3) and D(3√3, 0)
32. Find the ratio in which the point (-1, y) lying on the line segment joining points A(-3, 10) and (6, -8) divides it. Also, find the value of y.
Solution
Let k be the ratio in which P(-1, y) divides the line segment joining the points
A(-3, 10) and B(6, -8)
Then,
(-1, y) = {(k(6) – 3/(k + 1), (k(-8) + 10)/(k + 1)}
⇒ k(6) – 3}/(k + 1) = - 1 and y = {(k(-8) + 10}/(k + 1)
⇒ k = 2/7
Substituting k = 2/7 in y = {k(-8) + 10}/(k + 1), we get
y = {(-8 × 2)/7 + 10}/(2/7 + 1)
= (-16 + 70)/9
= 6
33. ABCD is rectangle formed by points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P, Q, R and S be the midpoints of AB, BC, CD and DA respectively, Show that PQRS is a rhombus.
Solution
Here the points P, Q, R and S are the midpoint of AB, BC, CD and DA respectively. Then,
Coordinates of P = (-1 – 1)/2, (-1 + 4)/2 = (-1, 3/2)
Coordinates of Q = (-1 + 5)/2, (4 + 4)/2 = (2, 4)
Coordinates of R = (5 + 5)/2, (4 – 1)/2 = (5, 3/2)
Coordinates of S = (- 1 + 5)/2, (-1 – 1)/2 = (2, -1)
Now,

Thus, PQ = QR = RS = SP and PR ≠ QS therefore PQRS is a rhombus.
34. The midpoint P of the line segment joining points A(-10, 4 and B(-2, 0) lies on the line segment joining the points C(-9, -4) and D(-4, y). Find the ratio in which P divides CD. Also, find the value of y.
Solution
The midpoint of AB is (-10 – 2)/2, (4 + 10)/2 = P(-6, 2)
Let k be the ratio in which P divides CD. So,
(-6, 2) = {k(-4) – 9}/(k + 1), {k(y) – 4)/(k + 1)
⇒ k(-4) – 9}/(k + 1) = - 6 and k(y) – 4}/(k + 1) = 2
⇒ k = 3/2
Now, substituting k = 3/2 in k(y) – 4}/(k + 1) = 2, we get
{y × 3/2 – 4}/(3/2 + 1) = 2
⇒ (3y – 8)/5 = 2
⇒ y = (10 + 8)/3 = 6
Hence, the required ratio is 3 : 2 and y = 6.
