RS Aggarwal Solutions Chapter 16 Coordinate Geometry Exercise 16A Class 10 Maths

Chapter Name | RS Aggarwal Chapter 16 Coordinate Geometry |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 16A Solutions
1. Find the distance between the points
(i) A(9, 3) and B(15, 11)
(ii) A (7,- 4) and B(-5, 1)
(iii) A(-6, - 4) and B(9, -12)
(iv) A(1, -3) and B (4, -6)
(v) P(a + b, a – b) and Q(a – b, a + b)
(vi) P(a sin α, α cos α) and Q(α cos α, - α sin α)
Solution
(i) A(9, 3) and B(15, 11)
The given points are A (9, 3) and B (15, 11)
Then (x1 = 9, y1 = 3) and (x2 = 15, y2 = 11)

(ii) A(7, -4) and B(-5, 1)
The given points are A(7, -4) and B(-5, 1)
Then, (x1 = 7, y1 = - 4) and (x2 = -5, y2 = 1)

(iii) A(-6, -4) and B(9, -12)
The given points are A(-6, -4) and B(9, -12)
Then (x1 = - 6, y1 = -4) and (x2 = 9, y2 = - 12)
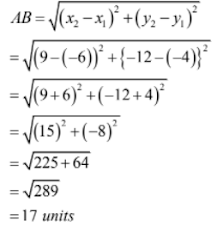
(iv) A(1, -3) and B(4, -6)
The given point are A(1, -3) and B(4, -6)
Then (x1 = 1, y1 = -3) and (x2 = 4, y2 = - 6)

(v) P(a + b, a – b) and Q(a – b, a + b)
The given points are P(a + b, a – b) and Q(a – b, a + b)
Then (x1 = a + b, y1 = a – b) and (x2 = a – b, y2 = a + b)

(vi) P(a sin α, a cos α) and Q(a cos α, -a sin α)
The given points are P(a sin α, a cos α) and Q(a cos α, - a sin α)
Then (x1 = a sin α, y1 = a cos α) and (x2 = a cos α, y2 = -a sin α)

(i) A(5, -12)
(ii) B(-5, 5)
(iii) C(-4, -6)
Solution
(i) A(5, -12)
Let O(0, 0) be the origin

(ii) B(-5, 5)
Let O(0, 0) be the origin.
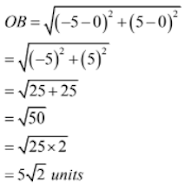
(iii) C(-4, -6)
Let O(0, 0) be the origin

Solution
Given AB = 5 units
Therefore, (AB)2 = 25 units
⇒ (5 – a)2 + {3 – (-1)}2 = 25
⇒ (5 – a)2 + (3 + 1)2 = 25
⇒ (5 – a)2 + (4)2 = 25
⇒ (5 – a)2 + 16 = 25
⇒ (5 – a)2 = 25 – 16
⇒ (5 – a)2 = 9
⇒ (5 – a) = ± √9
⇒ 5 – a = ±3
⇒ 5 – a = 3 or 5 – a = - 3
⇒ a = 2 or 8
Therefore, a = 2 or 8.
4. Find all possible values of y for which distance between the points A(2, -3) and B(10, y) is 10 units
Solution
The given points are A(2, -3) and B(10, y)

⇒ 73 + y2 + 6y = 100 [Squaring both sides)
⇒ y2 + 6y – 27 = 0
⇒ y2 + 9y – 3y – 27 = 0
⇒ y(y + 9) – 3(y + 9) = 0
⇒ (y + 9)(y – 3) = 0
⇒ y + 9 = 0 or y – 3 = 0
⇒ y = -9 or y = 3
Hence, the possible values of y are -9 and 3.
5. Find value of x for which the distance between the points P(x, 4) and Q(9, 10) is 10 units.
Solution
The given points are P(x, 4) and Q(9, 10).

⇒ x2 – 18x + 17 = 0
⇒ x2 – 17x – x + 17 = 0
⇒ x(x – 17) – 1(x – 17) = 0
⇒ (x – 17)(x – 1) = 0
⇒ x – 17 = 0 or x – 1 = 0
⇒ x = 17 or x = 1
Hence, the values of x are 1 and 17.
6. If the point A(x, 2) is equidistant from the points B(8, -2) and C(2, -2) , find the value of x. Also, find the value of x. Also, find the length of AB,
Solution
As per the question
AB = AC

Solution
As per the question
AB = AC

8. Find the point on the a-axis which is equidistant from the points (2, -5) and (-2, 9).
Solution
Let (x, 0) be the points on the x-axis. Then as per the question, we have

⇒ (x – 2)2 + (5)2 = (x + 2)2 + (-9)2 (Squaring both sides)
⇒ x2 – 4x + 4 + 25 = x2 + 4x + 4 + 81
⇒ 8x = 25 – 81
⇒ x = -(56/8) = - 7
Hence, the point on the x-axis is (-7, 0).
9. Find the points on the a-axis, each of which is at a distance of 10 units from the point A(11, -8).
Solution
Let P(x, 0) be the point on the x-axis. Then as per the question we have
AP = 10

⇒ (x – 11)2 + 82 = 100 (Squaring both sides)
⇒ (x – 11)2 = 100 – 64 = 36
⇒ x – 11 = ± 6
⇒ x = 11 ± 6
⇒ x = 11 – 6, 11 + 6
⇒ x = 5, 17
Here the points on the x-axis are (5, 0) and (17, 0).
10. Find the points on the y-axis which is equidistant from the points A(6, 5) and B(-4, 3)
Solution
Let P (0, y) be a point on the y-axis. Then as per the question, we have
AP = BP

⇒ (6)2 + (y – 5)2 = (4)2 + (y – 3)2 (Squaring both sides)
⇒ 36 + y2 – 10y + 25 = 16 + y2 – 6y + 9
⇒ 4y = 36
⇒ y = 9
Hence, the point on the y-axis is (0, 9).
11. If the points P(x, y) is a point equidistant from the points A(5, 1) and B(-1, 5), Prove that 3x = 2y.
Solution
As per the question, we have
AP = BP

⇒ (x – 5)2 + (y – 1)2 = (x + 1)2 + (y – 5)2 (Squaring both sides)
⇒ x2 – 10x + 25 + y2 – 2y + 1 = x2 + 2x + 1 + y2 – 10y + 25
⇒ - 10x – 2y = 2x – 10y
⇒ 8y = 12x
⇒ 3x = 2y
Hence, 3x = 2y
12. If p(x, y) is point equidistant from the points A(6, -1) and B(2, 3), show that x – y = 3
Solution
The given points are A(6, -1) and B(2, 3). The point P(X, y) equidistant from the points A and B So, PA = PB
Also, (PA)2 = (PB)2
⇒ (6 – x)2 + (-1 – y)2 = (2 – x)2 + (3 – y)2
⇒ x2 – 12x + 36 + y2 + 2y + 1 = x2 – 4x + 4 + y2 – 6y + 9
⇒ x2 + y2 – 12x + 2y + 37 = x2 + y2 – 4x – 6y + 13
⇒ x2 + y2 – 12x + 2y – x2 –y2 + 4x + 6y = 13 – 37
⇒ - 8x + 8y = - 24
⇒ -8(x – y) = - 24
⇒ x – y = -24/-8
⇒ x – y = 3
Hence proved.
13. Find the co-ordinates of the point equidistant from three given points A(5, 3), B(5, -5) and C(1, -5)
Solution
Let the required point be P(x, y). Then AP = BP = CP
That is, (AP)2 = (BP)2 = (CP)2
This means (AP)2 = (BP)2
⇒ (x – 5)2 + (y – 3)2 = (x – 5)2 + (y + 5)2
⇒ x2 – 10x + 25 + y2 – 6y + 9 = x2 – 10x + 25 + y2 + 10y + 25
⇒ x2 – 10x + y2 – 6y + 34 = x2 – 10x + y2 + 10y + 50
⇒ x2 – 10x + y2 – 6y – x2 + 10x – y2 – 10y = 50 – 34
⇒ -16y = 16
⇒ y = -16/16 = - 1
And (BP)2 = (CP)2
⇒ (x – 5)2 + (y + 5)2 = (x – 1)2 + (y + 5)2
⇒ x2 – 10x + 25 + y2 + 10y + 25 = x2 – 2x + 1 + y2 + 10y + 25
⇒ x2 – 10x + y2 + 10y + 50 = x2 – 2x + y2 + 10y + 26
⇒ x2 – 10x + y2 + 10y – x2 + 2x – y2 – 10y = 26 – 50
⇒ -8x = - 24
⇒ x = -24/-8 = 3
Hence, the required point is (3, -1).
14. If the points A(4, 3) and B(x, 5) lies on a circle with the centre O(2, 3). Find the value of x.
Solution
Given, the points A(4, 3) and B(x, 5) lie on the a circle with center O(2, 3).
Then OA = OB
Also (OA)2 = (OB)2
⇒ (4 - 2)2 + (3 – 3)2 = (x – 2)2 + (5 – 3)2
⇒ (2)2 + (0)2 = (x – 2)2 + (2)2
⇒ 4 = (x – 2)2 + 4
⇒ (x – 2)2 = 0
⇒ x = 2
Therefore, x = 2
15. If the point C(-2, 3) is equidistant from the points A(3, -1) and B(x, 8), find the value of x. Also, find the distance between BC.
Solution
As per the question, we have
AC = BC

16. If the point P(2, 2) is equidistant from the points A(-2, k) and B(-2k, -3), find k. Also, find the length of AP.
Solution
As per the question, we have
AP = BP

17. If the point (x, y) is equidistant from the points (a + b, b – a) and (a – b, a + b), prove that bx = ay.
Solution
As per the question, we have

⇒ (x – a – b)2 + (y – b + a)2 = (x – a + b)2 + (y – a – b)2 (Squaring both sides)
⇒ x2 + (a + b)2 – 2x(a + b) + y2 + (a – b)2 – 2y(a – b) = x2 + (a – b)2 – 2x(a – b) + y2 + (a + b)2 – 2y(a – b)
⇒ -x(a + b) – y(a – b) = -x(a – b) – y(a + b)
⇒ -xa – xb – ay + by = - xa + bx – ya – by
⇒ by = bx
Hence, bx = ay.
18. Using the distance formula, show that the given points are collinear.
(i) (1, -1), (5, 2) and (9, 5)
(ii) (6, 9), (0, 1) and (-6, -7)
(iii) (-1, -1), (2, -3) and (8, 11)
(iv) (-2, 5), (0, 1) and (2, -3)
Solution
(i) Let A(1, -1), B(5, 2) and C(9, 5) be the give points. Then

∴ AB + BC = (5 + 5) units = 10 units = AC
Hence, the given points are collinear.
(ii) Let A(6, 9), B(0, 1) and C(-6, -7) be the give points. Then

∴ AB + BC = (10 + 10) units = 20 units = AC
Hence, the given points are collinear
(iii) Let A(-1, -1), B(2, 3) and C(8, 11) be the give points. Then

∴ AB + BC = (5 + 10) units = AC
Hence, the given points are collinear.
(iv) Let A(-2, 5), B(0, 1) and C(2, -3) be the given points. Then
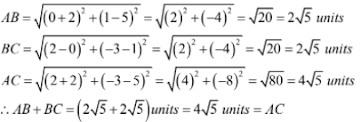
∴ AB + BC = (2√5 + 2√5) units = 4√5 units = AC
Hence, the given points are collinear.
19. Show that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
Solution
The given points are A(7, 10), B(-2, 5) and (3, -4)

Thus, (AB)2 + (BC)2 = (AC)2
This show that △ABC is right-angles at B.
Therefore, the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right-angled triangle.
20. Show that the points A(3, 0) and B(6, 4) and C(-1, 3) are the vertices of an isosceles right triangle.
Solution
The given points are A(3, 0), B(6, 4) and C(-1, 3). Now,

∵ AB = AC and AB2 + AC2 = BC2
Therefore, A(3, 0), B(6, 4) and C(-1, 3) are die vertices of an isosceles right triangle.
21. If A(5, 2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B = 90°, then find the value of t.
Solution
∵ ∠B = 90°
∴ AC2 = AB2 + BC2
⇒ (5 + 2)2 + (2 – t)2 = (5 – 2)2 + (2 + 2)2 + (2 + 2)2 + (2 – t)2
⇒ (7)2 + (t – 2)2 = (3)2 + (4)2 + (4)2 + (t + 2)2
⇒ 49 + t2 – 4t + 4 = 9 + 16 + 16 + t2 + 4t + 4
⇒ 8 – 4t = 4t
⇒ 8t = 8
⇒ t = 1
Hence, t = 1.
22. Prove that the points A(2, 4), B(2, 6) and C(2 + √3, 5) are the vertices of an equilateral triangle.
Solution
The given points are A(2, 4), B(2, 6) and C(2 + √3, 5). Now

Hence, the points A(2, 4), B(2, 6) and C(2 + √3, 5) are the vertices of an equilateral triangle.
23. Show that the points (-3, -3), (3, 3) and C(-3√3, 3√3) are the vertices of an equilateral triangle.
Solution
Let the given points be A(-3, -3), B(3, 3) and C(-3√3, 3√3). Now

Hence, the given points are the vertices of an equilateral triangle.
24. Show that the points A(-5, 6), B(3, 0) and C(9, 8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Solution
Let the given points be A(-5, 6) , B(3, 0) and C(9, 8).

Therefore, AB = BC = 10 units
Also, (AB)2 + (BC)2 = (10)2 + (10)2 = 200
and (AC)2 = (10√2)2 = 200
Thus, (AB)2 + (BC)2 = (AC)2
This show that △ ABC is right angled at B.
Therefore, the points A(-5, 6) B(3, 0) and C(9, 8) are the vertices of an isosceles right-angled triangle.
Also, area of a triangle = 1/2 × base × height
If AB is the height and BC is the base,
Area = 1/2 × 10 × 10
= 50 square units
25. Show that the points O(0, 0), A(3, √3) and B(3, -3√3) are the vertices of an equilateral triangle. Find the area of this triangle.
Solution
The given points are O(0, 0), A(3, √3) and B(3, -√3)
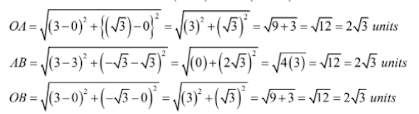
Therefore, OA = AB = OB = 2√3 units.
Thus, the points O(0, 0) A(3, √3) and B(3, -√3) are the vertices of an equilateral triangle
Also, the area of the triangle OAB = √3/4 × (side)2
= √3/4 × (2√3)2
= √3/4 × 12
= 3√3 square units.
26. Show that the following points are the vertices of a square:
(i) A(3, 2), B(0, 5), C(-3, 2) and D(0, -1)
(ii) A(6, -2), B(2, 1), C(1, 5) and D(5, 6)
(iii) A(0, -2), B(3, 1), C(0, 4) and D|(-3, 1)
Solution
(i) The given points are A(3, 2), B(0, 5), C(-3, 2) and D(0, -1)

Thus, diagonal AC = diagonal BD
Therefore, the given points from a square.
(ii) The given points are A(6, 2), B(2, 1), C(1, 5) and D(5, 6)

Thus, diagonal AC = diagonal BD
Therefore, the given points from a square.
(iii) The given points are P(0, -2), Q(3, 1), R(0, 4) and S(-3, 1)

Thus, diagonal PR = diagonal QS
Therefore, the given points from a square.
27. Show that the points A(-3, 2), B(-5, -5), C(2, -3) and D(4, 4) are the vertices of a rhombus. Find the area of this rhombus.
Solution
The given points are A(-3, 2), B(-5, -5), C(2, -3) and D(4, 4)

Thus, diagonal AC is not equal to diagonal BD.
Therefore, ABCD is a quadrilateral with equal sides and unequal diagonals
Hence, ABCD a rhombus.
Area of a rhombus = 1/2 × (product of diagonals)
= 1/2 × (5√2) × (9√2)
= 45(2)/2
= 45 square units.
28. Show that the points A(3, 0), B(4, 5), C(-1, 4) and D(-2, -1) are the vertices of a rhombus. Find its area.
Solution
The given points are A(3, 0), B(4, 5), C(-1, 4) and D(-2, -1)

Therefore, the given points are the vertices of a rhombus.
Area (ABCD) = 1/2 × AC × BD
= 1/2 × 4√2 × 6√2
= 24 sq. units
Hence, the area of the rhombus is 24 sq. units.
29. Show that the points A(6, 1), B(8, 2) and C(9, 4) and D(7, 3) are the vertices of a rhombus. Find its area.
Solution
The given points are A(6, 1), B(8, 2), C(9, 4) and D(7, 3)

∵ AB = BC = CD = AD = √5 and AC ≠ BD
Therefore, the given points are vertices of a rhombus. Now,
Area (ABCD) = 1/2 × AC × BD
= 1/2 × 3√2 × √2 = 3 sq units.
Hence, the area of the rhombus is 3 sq. units.
30. Show that the points A(2, 1), B(5, 2) , C(6, 4) and D(3, 3) are the angular points of a parallelogram. Is this figure a rectangle ?
Solution
The given points are A(2, 1), B(5, 2), C(6, 4) and D(3, 3)

Hence, the given points do not form a rectangle.
31. Show that A(1, 2), B(4, 3), C(6, 6) and D(3, 5) are the vertices of a parallelogram. Show that ABCD is not rectangle.
Solution
The given points are A(1, 2), B(4, 3),C(6, 6) and D(3, 5).

Thus, the diagonal AC and BD are not equal and hence ABCD is not a rectangle.
32. Show that the following points are the vertices of a rectangle.
(i) A(-4, -1),B(-2, -4), C(4, 0) and D(2, 3)
(ii) A(2, -2), B(14, 10), C(11, 13) and D(-1, 1)
(iii) A(0, -4), B(6, 2), C(3, 5) and D(-3, -1)
Solution
(i) The given points are A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3)
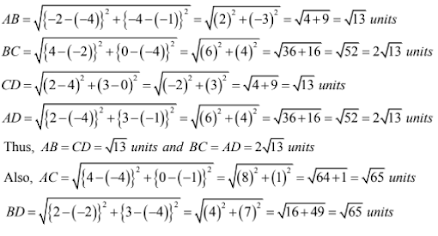
Hence, the given points from a rectangle.
(ii) The given points are A(2, -2), B(14, 10) C(11, 13) and D(-1, 1)

Also, diagonal AC = diagonal BD
Hence, the given points from a rectangle.
(iii) The given points are A(0, -4), B(6, 2), C(3, 5) and D(-3, 1)

Also, diagonal AC = diagonal BD
Hence, the given points from a rectangle.
