RS Aggarwal Solutions Chapter 14 Height and Distance Exercise 14A Class 10 Maths

Chapter Name | RS Aggarwal Chapter 14 Height and Distance |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 14A Solutions
1. A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take √3 = 1.732]
Solution
Let AB be the tower standing vertically on the ground and O be the position of the observer
We now have:
OA = 20 m, ∠OAB = 90° and ∠AOB = 60°
Let
AB = h m

Now, in the right ∆OAB, we have
AB/OA - tan 60° = √3
⇒ h/20 = √3
⇒ h = 20√3 = (20 × 1.732) = 36.64
Hence, the height of the pole is 34.64 m.
2. A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60° to the horizontal. Find the length of the string, assuming that there is no slack in it. [Take √3 = 1.732]
Solution
Let OX be the horizontal ground and A be the position of the kite.
Also, let O be the position of the observer and OA be the thread.
Now, draw AB ⊥ OX.
We have:
∠BOA = 60°, OA = 75 m and ∠OBA = 90°
Height of the kite from the ground = AB = 75 m
Length of the string OA = x m

AB/OA = sin 60° = √3/2
⇒ 75/x = √3/2
⇒ x = (75 × 2)/√3
= 150/1.732
= 86.6 m
Hence, the length of the string is 86.6 m.
3. An observer 1.5 m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60°. Find the height of the chimney.
Solution

We have,
BD = CE = 1.5 m, BC = DE = 30 m and ∠ACB = 60°
In ∆ABC
tan 60° = AB/BC
⇒ √3 = (AD – BD)/30
⇒ AD – 1.5 = 30√3
⇒ AD = 30√3 + 1.5
⇒ AD = 30 × 1.732 + 1.5
⇒ AD = 51.96 + 1.5
⇒ AD = 53.46 m
So, the height of the chimney is 53.46 m (approx.)
4. The angles of elevation of the top of a tower from two points at distance of 5 meters and 20 meters from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
Solution

We have,
AC = 5 m, AD = 20 m
Let the angle of elevation of the top of the tower (i.e., ∠ACB) from point C be θ.
Then, the angle of elevation of the top of the tower (i.e., Z ADB) from point D = (90° - θ)
Now, in ∆ABC
tan θ = AB/BC
⇒ tan θ = AB/5 …(i)
Also, in ∆ABD,
cot(90° - θ) = AD/AB
⇒ tan θ = 20/AB …(ii)
From (i) and (ii), we get
AB/5 = 20/AB
⇒ AB2 = 100

∴ AB = 10 m
So, the height of the tower is 10 m.
5. The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff [Use √3 = 1.732]
Solution

We have,
AB = 120 m, ∠BAC = 45°, ∠BAD = 60°
Let CD = x
In ∆ABC,
tan 45° = BC/AB
⇒ 1 = BC/120
⇒ BC = 120 m
Now, in ∆ABD,
tan 60° = BD/AB
⇒ √3 = (BC + CD)/120
⇒ BC + CD = 120√3
⇒ 120 + x = 120√3
⇒ x = 120√3 – 120
⇒ x = 120(√3 – 1)
⇒ x = 120 (1.732 – 1)
⇒ x = 120(0.732)
⇒ x = 87.84 ≈ 87.8 m
So, the height of the flagstaff is 87.8 m.
6. From a point on the 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30°. The angle of elevation of the top of a water tank (on the top of the tower) is 45°, Find (i) the height of the tower, (ii) the depth of the tank.
Solution

We have,
AB = 40 m, ∠BAC = 30° and ∠BAD = 45°
In ∆ABD
tan 45° = BD/AB
⇒ 1 = BD/40
⇒ BD = 40 m
Now, in ∆ABC,
tan 30° = BC/AB
⇒ 1/√3 = BC/40
⇒ BC = 40/√3
⇒ BC = 40/√3 × √3/√3
⇒ BC = (40√3)/3 m
(i) The height of the tower, BC = (40√3)/3 = (40 × 1.73)/3
= 23.067 ≈ 23.1 m
(ii) The depth of the tank, CD = (BD – BC)
= (40 – 23.1)
= 16.9 m
7. The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6 m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the flagstaff 60°. Find the height of the tower.
[Use √3 = 1.732]
Solution

We have,
BC = 6 m, ∠AOB = 30° and ∠AOC = 60°
Let AB = h
In ∆AOB
tan 30° = AB/OA
⇒ 1/√3 = h/OA
⇒ OA = h√3 ….(i)
Now, in ∆AOC,
tan 60° = AC/OA
⇒ √3 = (AB + BC)/h√3 [Using (i)]
⇒ 3h = h + 6
⇒ 3h – h = 6
⇒ 2h = 6
⇒ h = 6/2
⇒ h = 3 m
So, the height of the tower is 3 m.
8. A statue 1.46 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution
Let AC be the pedestal and BC be the statue such that BC = 1.46 m.
We have:
∠ADC = 45° and ∠ADB = 60°
Let:
AC = h m and AD = x m

AC/AD = tan 45° = 1
⇒ h/x = 1
⇒ h = x
Or,
x = h
Now, in the right ∆ADB, we have,
AB/AD = tan 60° = √3
⇒ (h + 1.46)/x = √3
On putting x = h in the above equation, we get
(h + 1.46)/h = √3
⇒ h + 1.46 = √3h
⇒ h(√3 – 1) = 1.46
⇒ h = 1.46/(√3 – 1) = 1.46/0.73 = 2m
Hence, the height of the pedestal is 2 m.
9. The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30°. How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60°.
Solution
Let AB be the unfinished tower, AC be the raised tower and O be the point of observation
We have:
OA = 75 m, ∠AOB = 30° and ∠AOC = 60°
Let AC = H m such that BC = (H – h)m.

AB/OA = tan 30° = 1/√3
⇒ h/75 = 1/√3
⇒ h = 75/√3 m = (75 × √3)/(√3 × √3)
= 25√3 m
In ∆AOC, we have:
AC/OA = tan 60° = √3
⇒ H/75 = √3
⇒ H = 75√3 m
∴ Required height = (H – h) = (75√3 - 25√3)
= 50√3 m
= 86.6 m.
10. On a horizontal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 metres away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
Solution
Let OX be the horizontal plane, AD be the tower and CD be the vertical flagpole
We have:
AB = 9 m, ∠DBA = 30° and ∠CBA = 60°
Let:
AD = h m and CD = x m

In the right ∆ABD, we have:
AD/AB = tan 30° = 1/√3
⇒ h/9 = 1/√3
⇒ h = √9/3 = 5.19 m
Now, in the ∆ABC, we have
AC/BA = tan 60° = √3
⇒ (h + x)/9 = √3
⇒ h + x = 9√3
By putting h = 9/√3 in the above equation, we get:
9/√3 + x = 9√3
⇒ x = 9√3 - 9/√3
⇒ x = (27 – 9)/√3 = 18/√3 = 10.4
Thus, we have:
Height of the flagpole = 10.4 m
Height of the tower = 5.19 m
11. Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide, from a point P between them on the road, the angle of elevation of the top of one pole is 60° and the angle of depression from the top of another pole at P is 30°. Find the height of each pole and distance of the point P From the poles.
Solution

We have:
∠AOB = 60° and ∠COD = 60°
In ∆AOB,
tan 60° = AB/BO
⇒ √3 = AB/BO
⇒ BO = AB/√3
Also, in ∆COD,
tan 30° = CD/DO
⇒ 1/√3 = CD/DO
⇒ DO = √3CD
⇒ DO = √3CD
As, BD = 80
⇒ BO + DO = 80
⇒ AB/√3 + √3CD = 80
⇒ AB/√3 + √3AB = 80 (Given AB = CD)
⇒ AB(1/√3 + √3) = 80
⇒ AB(1 + 3)/√3 = 80
⇒ AB(4/√3) = 80
⇒ AB = (80 + √3)/4
⇒ AB = 20√3 m
Also, BO = AB/√3 = 20√3/√3 = 20 m
So, DO = 80 – 20 = 60 m
Hence, the height of each pole is 20√3 m and point P is at a distance of 20 m from left pole and 60 m from right pole.
12. Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30° and 45° respectively. If the height of the tower is 50 metres, find the distance between the two men.
Solution
Let CD be the tower and A and B be the positions of the two men standing on the opposite sides.
Thus, we have:
∠DAC = 30°, ∠DBC = 45° and CD = 50 m
Let AB = x m and BC = y m such that AC = (x – y)m.

In the right ∆DBC, we have:
CD/BC = tan 45° = 1
⇒ 50/y = 1
⇒ y = 50 m
In the right ∆ACD, we have:
CD/AC = tan 30° = 1/√3
⇒ 50/(x – y) = 1/√3
⇒ x – y = 50√3
On putting y = 50 in the above equation, we get:
x – 50 = 50√3
⇒ x = 50 + 50√3 = 50(√3 + 1)
= 136.6 m
∴ Distance between the two men = AB = x = 136.6 m
13. From the point of a tower 100 m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45° respectively. Find the distance between the cars.
Solution

We have,
PQ = 100 m, ∠PQR = 30° and ∠PBQ = 45°
In ∆APQ,
tan 30° = PQ/AP
⇒ 1/√3 = 100/AP
⇒ AP = 100√3 m
Also, in ∆BPQ,
tan 45° = PQ/BP
⇒ 1 = 100/BP
⇒ BP = 100 m
Now, AB = AP + BP
= 100√3 + 100
= 100(√3 + 1)
= 100 × (1.73 + 1)
= 100 × 2.73
= 273 m
So, the distance between the cars is 273 m.
14. A straight highway leads to the foot of a tower, A man standing on the top of the tower observe c car at an angle of depression of 30° which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution

Solution
Let PQ be the tower,
We have:
∠PBQ = 60° and ∠PAQ = 30°
Let PQ = h, AB = x and BQ = y
In ∆APQ,
tan 30° = PQ/AQ
⇒ 1/√3 = h/(x + y)
⇒ x + y = h√3 …(i)
Also, in ∆BPQ,
tan 60° = PQ/BQ
⇒ √3 = h/y
⇒ h = y√3 …..(ii)
Substituting h = y√3 in (i), we get
x + y = √3(y√3)
⇒ x + y = 3y
⇒ 3y – y = x
⇒ 2y = x
⇒ y = x/2
As, speed of the car from A to B = AB/6 = x/6 units/sec
So, the time taken to reach the foot of the tower i.e Q from B = BQ/speed
= y/(x/6)
= (x/2)/(x/6)
= 6/2
= 3 sec.
So, the time taken to reach the foot of the tower from the given point is 3 seconds.
15. A TV tower stands vertically on a bank of canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from the point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.
Solution

We have:
AB = 20 m, ∠PAQ = 30°, BQ = x and PQ = h
In ∆PBQ,
tan 60° = PQ/BQ
⇒ √3 = h/x
⇒ h = x√3 ….(i)
Again in ∆APQ,
tan 30° = PQ/AQ
⇒ 1/√3 = h/(AB + BQ)
⇒ 1/√3 = x√3/(20 + 3) [Using (i)]
⇒ 3x = 20 + x
⇒ 3x – x = 20
⇒ 2x = 20
⇒ x = 20/2
⇒ x = 10 m
Substituting x = 10 in (i), we get
h = 10√3m
So, the height of the TV tower is 10√3 m and the width of the canal is 10 m.
16. The angle of elevation on the top of a building from the foot of a tower is 30°. The angle of elevation of the top of the tower when seen from the top of the second water is 60°. If the tower is 60 m high, find the height of the building.
Solution

We have,
PQ = 60 m, ∠APB = 30°, ∠PAQ = 60°
In ∆APQ,
tan 60° = PQ/AP
⇒ √3 = 60/AP
⇒ AP = 60/√3
⇒ AP = (60√3)/3
⇒ AP = 20√3 m
Now, in ∆ABP,
tan 30° = AB/AP
⇒ 1/√3 = AB/20√3
⇒ AB = (20√3)/√3
∴ AB = 20 m
So, the height of the building is 20 m.
17. The horizontal distance between two towers is 60 metres. The angle of depression of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 90 metres. Find the height of the first tower.
Solution
Let DE be the first tower and AB be the second tower.
Now, AB = 90 m and AD = 60 m such that CE = 60 m and ∠BEC = 30°.
Let DE = h m such that AC = h m and BC = (90 – h) m.

In the right ∆BCE, we have:
BC/CE = tan 30° = 1/√3
⇒ (90 – h)/60 = 1/√3
⇒ (90 – h)√3 = 60
⇒ h√3 = 90√3 – 60
⇒ h = 90 – 60/√3
= 90 – 34.64
= 55.36 m.
∴ Height of the first tower = DE = h = 55.36 m
18. The angle of elevation of the top of a chimney from the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°. If the height of the tower is 40 metres. Find the height of the chimney.
Solution

We have:
AB = 40 m, ∠APB = 30° and ∠PAQ = 60°
In ∆ABP,
tan 30° = AB/AP
⇒ 1/√3 = 40/AP
⇒ AP = 40√3 m
Now, in ∆APQ,
tan 60° = PQ/AP
⇒ √3 = PQ/40√3
∴ PQ = 120 m
So, the height of the chimney is 120 m.
Hence, the height of the chimney meets the pollution norms.
In this question, management of air pollution has been shown.
19. From the top of a 7 meter high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution

We have,
AB = 7 m, ∠CAE = 60°, ∠DAE = ∠ADB = 45°
Also, DE = AB = 7 m
In ∆ABD,
tan 45° = AB/BD
⇒ 1 = 7/BD
⇒ BD = 7 m
So, AE = BD = 7 m
Also, in ∆ACE,
tan 60° = CE/AE
⇒ √3 = CE/7
⇒ CE = 7√3 m
Now, CD = CE + DE
= 7√3 + 7
= 7(√3 + 1) m
= 7(1.732 + 1)
= 7(2.732)
= 19.124
= 19.12 m
So, the height of the tower is 19.12 m.
20. The angle of depression form the top of a tower of a point A on the ground is 30°. On moving a distance of 20 metres from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60°. Find the height of the tower and its distance from the point A.
Solution

We have,
AB = 20 m, ∠PAQ = 30° and ∠PBQ = 60°
Let BQ = x and PQ = h
In ∆PBQ,
tan 60° = PQ/BQ
⇒ √3 = h/x
⇒ h = x√3 ….(i)
Also, in ∆APQ,
tan 30° = PQ/AQ
⇒ 1/√3 = h/(AB + BQ)
⇒ 1/√3 = x√3/(20 + x) [Using (i)]
⇒ 20 + x = 3x
⇒ 3x – x = 20
⇒ 2x = 20
⇒ x = 20/2
⇒ x = 10 m
From (i),
h = 10√3 = 10 × 1.732 = 17.32 m
Also, AQ = AB + BQ = 20 + 10 = 30 m
So, the height of the tower is 17.32 m and its distance from the point A is 30 m.
21. The angle of elevation of the top of a vertical tower from appoint on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 30°. Find the height of the tower.
Solution

We have,
AB = 10 m, ∠MAP = 30° and ∠PBQ = 60°
Also, MQ = AB = 10 m
Let BQ = x and PQ = h
So, AM = BQ = x and PM = PQ – MQ – h – 10
In ∆BPQ,
tan 60° = PQ/BQ
⇒ √3 = h/x
⇒ x = h/√3 ….(i)
Now, in ∆AMP,
tan 30° = PM/AM
⇒ 1/√3 = (h – 10)/x
⇒ h√3 - 10√3 = x
⇒ h√3 - 10√3 = h/√3 [Using (i)]
⇒ 3h – 30 = h
⇒ 3h – h = 30
⇒ 2h = 30
⇒ h = 30/2
∴ h = 15 m
So, the height of the tower is 15 m.
22. The angles of depression of the top and bottom of a tower as seen from the top of a 60√3 m high cliff are 45° and 60° respectively. Find the height of the tower.
Solution

We have,
BC = 60√3, ∠CDE = 45° and ∠BAC = 60°
Let AD = h
⇒ BE = AD = h
⇒ CE = BC – BE = 60√3 – h
In ∆CDE,
tan 45° = CE/DE
⇒ 1 = (60√3 – h)/DE
⇒ DE = 60√3 – h
⇒ AB = DE = 60√3 – h ….(i)
Now, in ∆ABC,
tan 60° = BC/AB
⇒ √3 = 60√3/(60√3 – h) [Using (i)]
⇒ 180 - h√3 = 60√3
⇒ h√3 = 180 - 60√3
⇒ h = (180 - 60√3)/√3 × √3/√3
⇒ h = (180√3 – 180)/3
⇒ h = 180(√3 – 1)/3
∴ h = 60(√3 – 1)
= 60(1.732 – 1)
= 60(0.732)
Also, h = 43.92 m
So, the height of the tower is 43.92 m
23. A man on the deck of a ship, 16 m above water level, observe that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30°. Calculate the distance of the cliff from the ship and height of the cliff.
Solution
Let AB be the deck of the ship above the water level and DE be the cliff.
Now,
AB = 16 m such that CD = 16 m and ∠BDA = 30° and ∠EBC = 60°
If AD = x m and DE = h m, then, CE = (h – 16)m.

In the right ∆BAD, we have
AB/AD = tan 30° = 1/√3
⇒ 16/x = 1/√3
⇒ x = 16√3 = 27.68 m
In the right ∆EBC, we have:
EC/BC = tan 60° = √3
⇒ (h – 16)/x = √3
⇒ h – 16 = x√3
⇒ h – 16 = 16√3 × √3 = 48 [∵ x = 16√3]
⇒ h = 48 + 16 = 64 m
∴ Distance of the cliff from the deck of the ship = AD = x = 27.68 m.
And,
Height of the cliff = DE = h = 64 m
24. The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation is 45°. Find the height of tower PQ.
Solution

XY = 40 m, ∠PXQ = 60° and ∠MYQ = 45°
Let PQ = h
Also, MP = XY = 40 m, MQ = PQ – MP = h – 40
In ∆MYQ,
tan 45° = MQ/MY
⇒ 1 = (h – 40)/MY
⇒ MY = h – 40
⇒ PX = MY = h – 40 …..(i)
Now, in ∆MXQ,
tan 60° = PQ/PX
⇒ √3 = h/(h – 40) [From (i)]
⇒ h√3 - 40√3 = h
⇒ h√3 – h = 40√3
⇒ h(√3 – 1) = 40√3
⇒ h = 40√3/(√3 – 1)
⇒ h = 40√3/(√3 – 1) × (√3 + 1)/(√3 + 1)
⇒ h = 40√3(√3 + 1)/(3 – 1)
⇒ h = [40√3(√3 + 1)]/2
⇒ h = 20√3(√3 + 1)
⇒ h = 60 + 20√3
⇒ h = 60 + 20 × 1.73
⇒ h = 60 + 34.6
∴ h = 94.6 m
So, the height of the tower PQ is 94.6 m.
25. The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 2500 meters, find the speed of the aeroplane.
Solution

We have.
PQ = BC = 2500 m, ∠PAQ = 45° and ∠BAC = 30°
In ∆PAQ,
tan 45° = PQ/AQ
⇒ 1 = 2500/AQ
⇒ AQ = 2500 m
Also, in ∆ABC,
tan 30° = BC/AC
⇒ 1/√3 = 2500/AC
⇒ AC = 2500√3 m
Now, QC = AC – AQ
= 2500√3 – 2500
Now, QC = AC – AQ
= 2500√3 – 2500
= 2500(√3 – 1)m
= 2500(1.732 – 1)
= 2500(0.732)
= 1830 m
⇒ PB = QC = 1830 m
So, the speed of the aero-plane = PB/15
= 1830/15
= 122 m/s
122 × 3600/1000 km/h
= 439.2 km/h
So, the speed of the aero-plane is 122m/s or 439.2 km/h.
26. The angle of elevation of the top of a tower from to point on the same level as the foot of the tower is 30°. On advancing 150 m towards foot of the tower, the angle of elevation becomes 60°. Show that the height of the tower is 129.9 metres.
Solution
Let AB be the tower
We have:
CD = 150 m, ∠ACB = 30° and ∠ADB = 60°
Let:
AB = h m and BD = x m

In right ∆ABD, we have:
AB/AD = tan 60° = √3
⇒ h/x = √3
⇒ x = h/√3
Now, in the right ∆ACB, we have:
AB/AC = tan 30° = 1/√3
⇒ h/(x + 150) = 1/√3
⇒ √3h = x + 150
On putting x = h/√3 in the above equation, we get:
√3h = h/√3 + 150
⇒ 3h = h + 150√3
⇒ 2h = 150√3
⇒ h = 150√3/2
= 75√3
= 75 × 1.732
= 129.9 m
Hence, the height of the tower is 129.9 m
27. As observed form the top of a lighthouse, 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60°. Determine the distance travelled by the ship during the period of observation.
Solution
Let OA be the lighthouse and B and C be the positions of the ship.
Thus, we have:
OA = 100 m, ∠OBA = 30° and ∠OCA = 60°

Let
OC = x m and BC = y m
In the right ∆OAC, we have
OA/OC = tan 60° = √3
⇒ 100/x = √3
⇒ x = 100/√3 m
Now, in the right ∆OBA, we have:
OA/OB = tan 30° = 1/√3
⇒ 100/(x + y) = 1/√3
⇒ x + y = 100√3
On putting x = 100/√3 in the above equation, we get:
y = 100√3 – 100/√3
= (300 – 100)/√3
= 200/√3
= 115.47 m
∴ Distance travelled by the ship during the period of observation = B = y = 115.47 m
28. From a point on a bridge across a river, the angles of depression of the bank on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 2.5 m from the banks, find the width of the river.
Solution

Thus, we have:
DP = 2.5, ∠PAD = 30° and ∠PBD = 45°
In the right ∆APD, we have
DP/AD = tan 30° = 1/√3
⇒ 2.5/AD = 1/√3
⇒ AD = 2.5/√3 m
In the right ∆PDB, we have:
DP/BD = tan 45° = 1
⇒ 2.5/BD = 1
∴ Width of the river = AB = (AD + BD)
= (2.5√3 + 2.5)
= 6.83 m
29. The angle of elevation of the top of a tower from to points at distances of 4m and 9 m from the base of the tower and in the same straight line with it are complementary. Show that the height of the tower is 6 metres.
Solution
Let AB be the tower and C and D be two points such that AC = 4 m and AD = 9 m
Let:
AB = h m, ∠BCA = θ and ∠BDA = 90° - θ

In the right ∆BCA, we have:
tan θ = AB/AC
⇒ tan θ = h/4 …(i)
In the right ∆BDA, we have:
tan (90° - θ) = AB/AD
⇒ cot θ = h/9 [tan (90° - θ) = cot θ]
⇒ 1/tan θ = h/9 ….(2) [cot θ = 1/tan θ]
Multiplying equations (1) and (2) ,we get
tan θ × 1/tan θ = h/4 × h/9
⇒ 1 = h2/36
⇒ 36 = h2
⇒ h = ± 6
Height of a tower cannot be negative.
∴ Height of the tower = 6 m
30. A ladder of length 6 metres an angle of 45° with the floor while learning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the distance between two walls of the room.
Solution
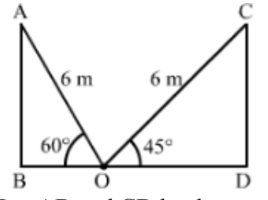
We have,
AO = CO = 6 m, ∠AOB = 60° and ∠COD = 45°
In ∆ABO,
cos 60° = BO/AO
⇒ 1/2 = BO/6
⇒ BO = 6/2
⇒ BO = 3 m
Also, in ∆CDO,
cos 45° = DO/CO
⇒ 1/√2 = DO/6
⇒ DO = 6/√2 × √2/√2
⇒ DO = (6√2)/2
⇒ DO = 3√2 m
Now, the distance between two walls of the room = BD
= BO + DO
= 3 + 3√2
= 3(1 + √2)
= 3(1 + 1.414)
= 3(2.414)
= 7.242 ≈ 7.24 m
So, the distant between two walls of the room is 7.24 m.
31. From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60°. If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
Solution

Let OP be the tower and points A and B be the positions of the cars.
We have:
AB = 100 m, ∠OAP = 60° and ∠OBP = 45°
Let OP = h
In ∆AOP,
tan 60° = OP/OA
⇒ √3 = h/OA
⇒ OA = h/√3
Also, in ∆BOP,
tan 45° = OP/OB
⇒ 1 = h/OB
⇒ OB = h
Now, OB – OA = 100
⇒ h – h/√3 = 100
⇒ (h√3 – h)/√3 = 100
⇒ h(√3 – 1)/√3 = 100
⇒ h = 100√3/(√3 – 1) × (√3 + 1)/(√3 + 1)
⇒ h = 100√3(√3 + 1)/(3 – 1)
⇒ h = 100(3 + √3)/2
⇒ h = 50(3 + 1.732)
⇒ h = 50(4.732)
∴ h = 236.6 m
So, the height of the tower is 236.6 m
Disclaimer. The answer given in the textbook is incorrect. The same has been rectified above.
32. An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
Solution

We have,
AC = 4 m, AB = 1 m, ∠BDC = 60°
And, BC = AC – AB = 4 – 1 = 3 m
In ∆BDC,
sin 60° = BC/BD
⇒ √3/2 = 3/BD
⇒ BD = (3 × 2)/√3
⇒ BD = 2√3
⇒ BD = 2 × 1.73
∴ BD = 3.46 m
So, he should use 3.46 m long ladder to reach the required position.
33. From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to the 30° and 60° respectively. Find
(i) The horizontal distance between AB and CD,
(ii) The height of the lamp post,
(iii) the difference between the heights of the building of the building and the lamp post.
Solution

AB = 60 m, ∠ACE = 30° and ∠ADB = 60°
Let BD = CE = x and CD = BE = y
⇒ AE = AB – BE = 60 – y
In ∆ACE,
tan 30° = AE/CE
⇒ 1/√3 = (60 – y)/x
⇒ x = 60√3 - y√3 ….(i)
Also, in ∆ABD,
tan 60° = AB/BD
⇒ √3 = 60/x
⇒ x = 60/√3
⇒ x = 60/√3 × √3/√3
⇒ x = (60 - √3)/3
⇒ x = 20√3
Substituting x = 20√3 in (i), we get
20√3 = 60√3 - y√3
⇒ y√3 = 60√3 - y√3
⇒ y√3 = 40√3
⇒ y = 40√3/√3
⇒ y = 40 m
(i) The horizontal distance between AB and CD = BD = x
= 20√3
= 20 × 1.732
= 34.64 m
(ii) The height of the lamp post = CD = y = 40 m
(iii) The difference between the heights of the building and the lamp post = AB – CD
= 60 – 40
= 20 m
