RS Aggarwal Class 10 Solutions Chapter 13 Construction Exercise 13B

RS Aggarwal Solutions Chapter 13 Construction Exercise 13B Class 10 Maths

Chapter Name	RS Aggarwal Chapter 13 Construction
Book Name	RS Aggarwal Mathematics for Class 10
Other Exercises	Exercise 13A
Related Study	NCERT Solutions for Class 10 Maths

Exercise 13B Solutions

1. Draw a circle of radius 3 cm. From a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure, the lengths of the tangents.

Solution

Steps of Construction

Step 1: Draw a circle with O as center and radius 3 cm.

Step 2: Mark a point P outside the circle such that OP = 7 cm.

Step 3: Join OP. Draw the perpendicular bisector XY of OP. cutting OP at Q.

Step 4: Draw a circle with Q as center and radius PQ (or OQ), to intersect the given circle at the points T and T’.

Step 5: Join PT and PT’.

Here, PT and PT’ are the required tangents.

PT = PT’ = 6.3 cm (Approx)

2. Draw two tangents to a circle of radius 3.5 cm from a point P at a distance of 6.2 cm from its centre.

Solution

Steps of Construction

Step 1: Draw a circle with O as center and radius 3.5 cm.

Step 2: Mark a point P outside the circle such that OP = 6.2 cm.

Step 3: Join OP. Draw the perpendicular bisector XY of OP, cutting OP at Q.

Step 4: Draw a circle with Q as center and radius PQ (or OQ), to intersect the given circle at the points T and T’.

Step 5: Join PT and PT’.

Here, PT and PT’ are the required tangents.

3. Draw a circle of radius 3.5 cm. Take two point A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.

Solution

Steps of Construction:

Step 1: Draw a circle with center O and radius 3.5 cm.

Step 2: Extends its diameter on both sides and mark two points A and B on it such that OA = OB = 5 cm.

Step 3: Draw the perpendicular bisectors of OA and OB. Let C and D be the mid-points of OA and OB, respectively.

Step 4: Draw a circle with C as center and radius OC (or AC), to intersect the circle with centre O, at the points P and Q.

Step 5: Draw another circle with D as center and radius OD (or BD), to intersect the circle with center O at the points R and S.

Step 6: Join AP and AQ, Also, join BR and BS.

Here, AP and AQ are the tangents to the circle from A. Also, BR and BS are the tangents to the circle from B.

4. Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.

Solution

Step 1: Draw a circle with center O and radius 4 cm.

Step 2: Draw any diameter AOB of the circle.

Step 3: At A, draw ∠OAX = 90°. Produce XA = Y.

Step 4: At B, draw ∠OBX’ = 90°. Produce X’B to Y’.

Here, XAY and X’BY’ are the tangents to the circle at the end points of the diameter AB.

5. Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents from the point P to the circle.

Solution

Steps of Construction:

Step 1: Draw a circle with the help of a bangle.

Step 2: Mark a point P outside the circle.

Step 3: Through P, draw a secant PAB to intersect the circle at A and B.

Step 4: Produce AP to C such that PA = PC.

Step 5: Draw a semicircle with CB as diameter.

Step 6: Draw PD ⊥ BC, intersecting the semicircle at D.

Step 7: With P as center and PD as radius, draw arcs to intersect the circle at T and T’.

Step 8: Join PT and PT’S.

Here, PT and PT’ are the required pair of tangents.

6. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

Solution

Steps of Construction:

Step 1: Draw a line segment AB = 8 cm.

Step 2: With A as center and radius 4 cm, draw a circle.

Step 3: With B as center and radius 3 cm, draw another circle.

Step 4: Draw the perpendicular bisector XY of AB, cuffing AB at C.

Step 5: With C as center and radius AC (or BC), draw a circle intersecting the circle with center A at P and P’: and the circle with center B at Q and Q’.

Step 6: Join BP and BP’. Also, join AQ and AQ’.

Here, AQ and AQ’ are the tangents from A to the circle with center B. Also, BP and BP’ are the tangents from B to the circle with center A.

7. Draw a circle of radius 4.2. Draw a pair of tangents to this circle inclined to each other at an angle of 45°.

Solution

Steps of Construction:

Step 1: Draw a circle with center O and radius = 4.2 cm

Step 2: Draw any diameter AOB of this circle.

Step 3: Construct ∠BOC = 45°, Such that the radius OC meets the circle at C.

Step 4: Draw AM ⊥ AB and CN ⊥ OC.

AM and CN intersect at P.

Thus, PA and PC are the required tangents to the given circle inclined at an angle of 45°.

8. Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°.

Solution

Steps of Construction:

Step 1: Draw a circle with center O and radius 3 cm.

Step 2: Draw any diameter AOB of the circle.

Step 3: Construct ∠BOC = 60° such that radius OC cuts the circle at C.

Step 4: Draw AM ⊥ AB and CN ⊥ OC. Suppose AM and CN intersect each other at P.

Here, AP and CP are the pair of tangents to the circle inclined to each other at angle of 60°.

9. Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle of 30° with a line passing through the centre.

Solution

Steps of Construction:

Step 1: Draw a circle with center O and radius 3 cm.

Step 2: Draw radius OA and produce it to B.

Step 3: Make ∠AOP = 60°

Step 4: Draw PQ ⊥ OP, meeting OB at Q.

Step 5: Then, PQ is the desired tangent, such that ∠OQP = 30°.

10. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.

Solution

Steps of Construction:

Step 1: Mark a point O on the paper.

Step 2: With O as center and radii 4 cm and 6 cm, draw two concentric circles.

Step 3: Mark a point P on the outer circle.

Step 4: Join OP.

Step 5: Draw the perpendicular bisector XY of OP, cutting OP at Q.

Step 6: Draw a circle with Q as center and radius OQ (or PQ), to intersect the inner circle in points T and T’.

Step 7: Join PT and PT’.

Here, PT and PT’ are the required tangents.

PT = PT’ = 4.5 cm (Approx)

Verification by actual calculation

Join OT to form a right ∆OTP (Radius is perpendicular to the tangent at the point of contact)

In right ∆OTP,

(OP = 6 cm and OT = 4 cm)

11. Draw a line segment AB of lengths 5. 4 cm. Divide it into six equal parts, Write the steps of construction.

Solution

Steps of Construction:

Step 1: Draw a line segment AB = 5.4 cm.

Step 2: Draw a ray AX, making an acute angle, ∠BAX.

Step 3: Jong AX, mark 6 points, A₁, A₂, A₃, A₄, A₅ such that,

AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆.

Step 4: Join A₆B.

Step 5: Draw A₁C, A₂D, A₃D, A₄F and A₅A₆.

Thus, AB is divided into six equal parts.

12. Draw a line segment AB of length 6.5 cm and divided it in the ratio 4 : 7. Measure each of the two parts.

Solution

Steps of Construction.

Step 1: Draw a line segment AB = 6.5 cm.

Step 2: Draw a ray AX, making an acute angle ∠BAX.

Step 3: Join AX, mark (4 + 7) = 11 points A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, A₉, A₁₀, A₁₁ such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇= A₇A₈ = A₈A₉ = A₉A₁₀ = A₁₀A₁₁

Step 4: Join A₁₁B. .

Step 5: From A₃, draw A₄C || A₁₁B, meeting AB at C.

Thus, C is the point on AB, which divides it in the ratio 4 : 7.

Thus, AC : CB = 4 : 7

From the figure,

AC = 2.36 cm

CB = 4.14 cm

13. Construct a ∆ABC in which B = 6.5 cm, AB = 4.5 cm and ∠ABC = 60°

Solution

Steps of Construction:

Step 1: Draw a line segment BC = 6.5 cm.

Step 2: With B as center, draw an angle of 60°.

Step 3: With B as center and radius equal to 4.5 cm, draw an arc, cutting the angle at A

Step 4: Join AB and AC.

Thus, ∆ABC is obtained.

Step 5: Below BC, draw an acute ∠CBX.

Step 6: Along BX, mark off four points B₁, B₂, B₃, B₄ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄

Step 7: Join B₄C.

Step 8: From B₃, draw B₃D || B₄C meeting BC at D.

Step 9: From D, draw DE || CA, meeting AB at E.

Thus, ∆EBD is the required triangle, each of whose sides is 3/4 the corresponding sides of ∆ABC.

14. Construct a ∆ABC in which BC = 5 cm, ∠C = 60° and the altitude from A equal to 3 cm. Construct a ∆ADE similar to ∆ABC such that each side of ∆ADE is 3/2 times the corresponding side of ∆ABC. Write the steps of construction.

Solution

Steps of Construction:

Step 1: Draw the line l.

Step 2: Draw an angle of 90° at M on l

Step 3: Cut an arc of radius 3 cm on the perpendicular. Mark the point as A.

Step 4: With A as center, make an angle of 30° and let it cut l at C. We get ∠ACB = 60°.

Step 5: Cut an arc of 5 cm from C on l and mark the point as B.

Step 6: Join AB.

Thus, ∆ABC is obtained.

Step 7: Extend AB to D, such that BD = BC.

Step 8: Draw DE || BC, cutting AC produced to E.

Then, ∆ADE is the required triangle, each of whose sides is of the corresponding sides of ∆ABC.

15. Construct an isosceles triangle whose base is 9 cm and altitude 5 cm. Construct another triangle whose sides are 3/4 of the corresponding sides of the first isosceles triangle.

Solution

Steps of Construction:

Step 1: Draw a line segment BC = 9 cm

Step 2: With B as center, draw an arc each above and below BC.

Step 3: With C as center, draw an arc each above and below BC.

Step 4: Join their points of intersection to obtain the perpendicular bisector of BC. Let it intersect BC at D.

Step 5: From D, cut an arc of radius 5 cm and mark the points as A

Step 6: Join AB and AC

Thus ∆ABC is obtained.

Step 7: Below BC make an acute ∠CBX.

Step 8: Along BX, mark off four points B₁, B₂, B₃, B₄ such that BB₁ = B₁B₂ = B₂B₃ = B3B4

Step 9: Join B₄C.

Step 10: From B₃, draw B₂E || B₄C meeting BC at E.

Step 11: From E, draw EF || CA meeting AB at F.

Thus, ∆FBE is the required triangle, each of whose sides is 3/4 the corresponding sides of the first triangle.

16. Draw a ∆ABC, right-angled at B such that AB = 3 cm and BC = 4 cm. Now, Construct a triangle similar to ∆ABC, each whose sides is 7/5 times the corresponding side of ∆ABC.

Solution

Steps of Construction

Step 1: Draw a line segment BC = 4 cm

Step 2: With B as center draw an angle of 90°

Step 3: With B as center and radius equal to 3 cm cut an arc at the right angle and name it A

Step 4: Join AB and AC.

 Thus, ∆ABC is obtained.

Step 5: Extend BC to D, such that BD = 7/5 BC = 7/5(4) cm) = 5.6 cm

Step 6: Draw DE || CA cutting AB produced to E

Thus, ∆EBD is the required triangle, each of whose sides is 7/5 the corresponding sides of ∆ABC.

17. Draw a circle of radius 4.8 cm. Take a point P on it. Without using the centre of the circle, construct a tangent at the point P. Write the steps of Construction.

Solution

Steps of Construction:

Step 1: Draw a circle of radius 4.8 cm.

Step 2: Mark a point P on it:

Step 3: Draw any chord PQ.

Step 4: Take a point R on the major arc QP

Step 5: Join PR and RQ

Step 6: Draw ∠QPT = ∠PRQ

Step 7: Produce TP to T’ as shown in the figure.

TPT is the required tangent.

18. Draw a circle of radius 3.5 cm. Draw a pair of tangents to this circle which are inclined to each other at an angle of 60°. Write the steps of construction.

Solution

Steps of Construction:

Step 1: Draw a circle with center O and radius = 3.5 cm.

Step 2: Draw any diameter AOB of this circle

Step 3: Construct ∠BOC = 60°, such that the radius OC meets the circle at C.

Step 4: Draw MA ⊥ AB and NC ⊥ OC.

Let AM and CN intersect at P.

Then, PA and PC are the required tangents to the given circle that are inclined at an angle of 60°.

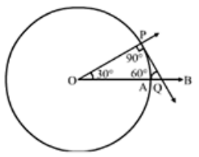
19. Draw a circle of radius 4 cm. Draw tangent to the circle making an angle of 60° with a line passing through the centre.

Solution

Steps of Construction:

Step 1: Draw a circle with centre O and radius 4 cm

Step 2: Draw radius OA and produce it to B.

Step 3: Make ∠AOP = 30°

Step 4: Draw PQ ⊥ OP, meeting OB at Q.

Step 5: Then, PQ is the desired tangent, such that ∠OQP = 60°

20. Draw two concentric circles of radii 4 cm and 6 cm. Construct a tangent to the smaller circle from a point on the larger circle. Measure the length of this tangent.

Solution

Steps of Construction:

Step 1: Draw a circle with O as center and radius 6 cm

Step 2: Draw another circle with O as center and radius 4 cm.

Step 3: Mark a point P on the circle with radius 6 cm

Step 4: Join OP and bisect it at M.

Step 5: Draw a circle with M as center and radius equal to MP to intersect the given circle with radius 4 cm at points T and T’.

Step 6: Join PT and PT’.

Thus, PT or PT’ the required tangents and measure 4.4 cm each.