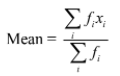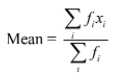RS Aggarwal Solutions Chapter 9 Mean, Mode and Median Exercise 9D Class 10 Maths

Chapter Name	RS Aggarwal Chapter 9 Mean, Mode and Median
Book Name	RS Aggarwal Mathematics for Class 10
Other Exercises	Exercise 9A Exercise 9B Exercise 9C Exercise 9E Exercise 9F
Related Study	NCERT Solutions for Class 10 Maths

Exercise 9D Solutions

1. Find the mean, median and mode of the following data:

Class	0 - 10	10 - 20	20 - 30	30 - 40	40 - 50	50 - 60	60 - 70
Frequency	4	4	7	10	12	8	5

Solution

To find the mean let us put the data in the table given below:

Class	Frequency (f_i)	Class mark (x_i)	f_i x_i
0 - 10	4	5	20
10 - 20	4	15	60
20 - 30	7	25	175
30 - 40	10	35	350
40 - 50	12	45	540
50 – 60	8	55	440
60 70	5	65	325
Total	Σf_i= 50		Σf_i x_i= 1910

= 1910/50

= 38.2

Thus, the mean of the given data is 38.2.

Now, to find the median let us put the data in the table given below:

Class	Frequency (f_i)	Cumulative Frequency (cf)
0 - 10	4	4
10 - 20	4	8
20 - 30	7	15
30 - 40	10	25
40 - 50	12	37
50 – 60	8	45
60 – 70	5	50
Total	N = Σf_i = 50

Now, N = 50

⇒ N/2 = 25

The cumulative frequency just greater than 25 is 37 and the corresponding class is 40 – 50.

Thus, the median class is 40 – 50.

∴ l = 40, h = 10, N = 50, f = 12 and cf = 25.

Now,

Median = l + ((N/2 – cf)/f) × h

= 40 + (25 – 25)/12 × 10

= 40.

Thus, the median is 40.

We know that,

Mode = 3(Median) – 2(Mean)

= 3 × 40 – 2 × 38.2

= 120 – 76.4

= 43.6

Hence, Mean = 38.2, Median = 40 and Mode = 43.6

2. Find the mean, median and mode of the following data:

Class	0 - 20	20 - 40	40 - 60	60 - 80	80 - 100	100 - 120	120 - 140
Frequency	6	8	10	12	6	5	3

Solution

To find the mean let us put the data in the table given below:

Class	Frequency (f_i)	Class mark (x_i)	f_ix_i
0 - 20	6	10	60
20 - 40	8	30	240
40 - 60	10	50	500
60 - 80	12	70	840
80 - 100	6	90	540
100 - 120	5	110	550
120 - 140	3	130	390
Total	Σf_i= 50		Σf_i x_i = 3120

= 3120/50

= 62.4

Thus, the mean of the given data is 62.4.

Now, to find the median let us put the data in the table given below:

Class	Frequency (f_i)	Cumulative Frequency (cf)
0 - 20	6	6
20 - 40	8	14
40 - 60	10	24
60 - 80	12	36
80 - 100	6	42
100 – 120	5	47
120 – 140	3	50
Total	N = Σf_i= 50

Now, N = 50

⇒ N/2 = 25

The cumulative frequency just greater than 25 is 36 and the corresponding class is 60 – 80.

Thus, the median class is 60 – 80.

∴ l = 60, h = 20, N = 50, f = 12 and cf = 24.

Now,

Median = l + ((N/2 – cf)/f) × h

= 60 + (25 – 24)/12 × 20

= 60 + 1.67

= 61.67

Thus, the median is 61.67.

We know that,

Mode = 3(Median) – 2(mean)

= 3 × 61.67 – 2 × 62.4

= 185.01 – 124.8

= 60.21

Hence, Mean = 62.4, Median = 61.67 and Mode = 60.21

3. Find the mean, median and mode of the following data:

Class	0 - 50	5 - 100	100 - 150	150 - 200	200 - 250	250 - 300	300 - 350
Frequency	2	3	5	6	5	3	1

Solution

To find the mean let us put the data in the table given below:

Class	Frequency (f_i)	Class mark (x_i)	f_i x_i
0 - 50	2	25	50
50 - 100	3	75	225
100 - 150	5	125	625
150 - 200	6	175	1050
200 - 250	5	225	1125
250 - 300	3	275	825
300 – 350	1	325	325
Total	Σf_i = 25		Σf_i x_i = 4225

= 4225/25

= 169

Thus, mean of the given data is 169.

Now, to find the median let us put the data in the table given below:

Class	Frequency (f_i)	Cumulative frequency (cf)
0 - 50	2	2
50 - 100	3	5
100 - 150	5	10
150 - 200	6	16
200 – 250	5	21
250 – 300	3	24
300 – 350	1	25
Total	N = Σf_i = 25

Now, N = 25, ⇒ N/2 = 12.5

The cumulative frequency just greater than 12.5 is 16 and the corresponding class is 150 – 200.

Thus, the median class is 150 – 200.

∴ l = 150, h = 50, N = 25, f = 6 and cf = 10.

Now,

Median = l + ((N/2 – cf)/f) × h

= 150 + (12.5 – 10)/6 × 50

= 150 + 20.83

= 170.83

Thus, the median is 170.83

We know that,

Mode = 3(Median) – 2(mean)

= 3 × 170.83 – 2 × 169

= 512.49 – 33.8

= 174.49

Hence, mean = 169, Median = 170.83 and Mode = 174.49

4. Find the mean, median and mode of the following data:

Marks Obtained	25 - 35	35 - 45	45 - 55	55 - 65	65 - 75	75 - 85
No. of students	7	31	33	17	11	1

Solution

To find the mean let us put the data in the table given below:

Marks Obtained	Number of students (f_i)	Class mark (x_i)	f_ix_i
25 - 35	7	30	210
35 - 45	31	40	1240
45 - 55	33	50	1650
55 - 65	17	60	1020
65 - 75	11	70	770
75 - 85	1	80	80
Total	Σf_i = 100		Σf_i x_i = 4970

= 4970/100

= 49.7

Thus, mean of the given data is 49.7.

Now, to find the median let us put the data in the table given below:

Class	Frequency (f_i)	Cumulative frequency (cf)
25 - 35	7	7
35 - 45	31	38
45 - 55	33	71
55 - 65	17	88
65 - 75	11	99
75 - 85	1	100
Total	N = Σf_i = 100

Now, N = 100 ⇒ N/2 = 50.

The cumulative frequency just greater than 50 is 71 and the corresponding class is 45 – 55.

Thus, the median class is 45 – 55.

∴ l = 45, h = 10, N = 100, f = 33 and cf = 38.

Now,

Median = l + ((N/2 – cf)/f) × h

= 45 + (50 – 38)/33 × 10

= 45 + 3.64

= 48.64

Thus, the median is 48.64

We know that,

Mode = 3(Median) – 2(mean)

= 3 × 48.64 – 2 × 49.70

= 145.92 – 99.4

= 46.52

Hence, Mean = 49.70, Median = 48.64 and Mode = 46.52

5. A survey regarding the heights (in cm) of 50 girls of a class was conducted and the following data was obtained:

Height in cm	120 - 130	130 - 140	140 - 150	150 - 160	160 - 170
No. of girls	2	8	12	20	8

Find the mean, median and mode of the above data.

Solution

We have the following:

Height in cm	Mid value (x_i)	Frequency (f_i)	Cumulative frequency	(f_i × x_i)
120 - 130	125	2	2	250
130 - 140	135	8	10	1080
140 - 150	145	12	22	1740
150 - 160	155	20	42	3100
160 - 170	165	8	50	1320
		Σf_i= 50		Σf_i × x_i = 7490

= 7490/50

= 149.8

Now, N = 50

⇒ N/2 = 25.

The cumulative frequency just greater than 25 is 42 and the corresponding class is 150 – 160.

Thus, the median class is 150 – 160.

∴ l = 150, h = 10, f = 20, c = cf of preceding class=22 and N/2 = 25

Now,

Median, Me = l + {h × ((N/2 – c)/f)}

= 150 + {10 × ((25 – 22)/20)}

= (150 + 10 × 3/20)

= 151.5

Mode = 3(median) – 2(Mean)

= 3 × 151.5 – 2 × 149.8

= 154.9

6. The following table gives the daily income of 50 workers of a factory:

Daily income (in Rs)	100 - 120	120 - 140	140 - 160	160 - 180	180 - 200
No. of workers	12	14	8	6	10

Find the mean, median and mode of the above data.

Solution

We have the following:

Daily income	Mid values (x_i)	Frequency (f_i)	Cumulative frequency	(f_i × x_i)
100 - 120	110	12	12	1320
120 - 140	130	14	26	1820
140 - 160	150	8	34	1200
160 - 180	170	6	40	1020
180 - 200	190	10	50	1900
		Σf_i = 50		Σf_i × x_i = 7260

= 7260/50

= 145.2

Now, N = 50

⇒ N/2 = 25

The cumulative frequency just greater than 25 is 26 and the corresponding class is 120 – 140.

Thus, the median class is 120 – 140.

∴ l = 120, h = 20, f = 14, c = cf of preceding class=12 and N/2 = 25

Now,

Median, M_e= l + {h × ((N/2 – c)/f)}

= 120 + {20 × (25 – 12)/14}

= (120 + 20 × 13/14)

= 138.57

Mode = 3(median) – 2(mean)

= 3 × 138.57 – 2 × 145.2

= 125.31

7. The table shows the daily expenditure on food of 30 households in a locality:

Daily expenditure (in Rs)	Number of households
100 - 150	6
150 - 200	7
200 - 250	12
250 - 300	3
300 - 350	2

Find the mean and median daily expenditure on food.

Solution

We have the following:

Daily expenditure (in Rs)	Mid value (x_i)	Frequency (f_i)	Cumulative frequency	(f_i× x_i)
100 - 150	125	6	6	750
150 - 200	175	7	13	1225
200 - 250	225	12	25	2700
250 - 300	275	3	28	825
300 - 350	325	2	30	650
		Σf_i = 30		Σf_i × x_i = 6150

= 6150/30

= 205

Now, N = 30

⇒ N/2 = 15

The cumulative frequency just greater than 15 is 25 and the corresponding class is 200 – 250.

Thus, the median class is 200 – 250.

∴ l = 200, h = 50, f = 12, c = cf of preceding class = 13 and N/2 = 15

Now,

Median, M_e = l + {h × (N/2 – c)/f)}

= 200 + {50 + (15 – 13)/12)}

= (200 + 50 × 2/12)

= 200 + 8.33

= 208.33

RS Aggarwal Solutions Chapter 9 Mean, Mode and Median Exercise 9D Class 10 Maths

Exercise 9D Solutions

About Us

Contact Form

RS Aggarwal Class 10 Solutions Chapter 9 Mean, Mode and Median Exercise 9D

RS Aggarwal Solutions Chapter 9 Mean, Mode and Median Exercise 9D Class 10 Maths

Exercise 9D Solutions

You might like

Contact Form