RS Aggarwal Solutions Chapter 4 Triangles Exercise - 4D Class 10 Maths
Chapter Name | RS Aggarwal Chapter 4 Triangles |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 4D Solutions
1. The sides of certain triangles are given below. Determine which of them right triangles are.
(i) 9cm, 16cm, 18cm
(ii) 7cm, 24cm, 25cm
(iii) 1.4cm, 4.8cm, 5cm
(iv) 1.6cm, 3.8cm, 4cm
(v) (a – 1) cm, 2√a cm, (a + 1) cm
Solution
For the given triangle to be right-angled, the sum of the two sides must be equal to the square of the third side.
Here, let the three sides of the triangle be a, b and c.
(i) a = 9 cm, b = 16 cm and c = 18 cm
Then,
a2 + b2 = 92 + 162 = 81 + 256
= 337
c2 = 192
= 361
a2 + b2 ≠ c2
Thus, the given triangle is not right-angled.
(ii) a = 7 cm, b = 24 cm and c = 25 cm
Then,
a2 + b2 = 72 + 242
= 49 + 576
= 625
c2 = 252
= 625
a2 + b2 = c2
Thus, the given triangle is a right-angled.
(iii) a = 1.4 cm, b= 4.8 cm and c= 5 cm
Then,
a2 + b2 = (1.4)2 + (4.8)2
= 1.96 + 23.04
= 25
c2 = 52
= 25
a2 + b2 = c2
Thus, the given triangle is right-angled.
(iv) a = 1.6 cm, b = 3.8 cm and c = 4 cm
Then
a2 + b2 = (1.6)2 + (3.8)2
= 2.56 + 14.44
= 16
a2 + b2 ≠ c2
Thus, the given triangle is not right-angled.
(v) p = (a - 1) cm, q = 2 √a cm and r = (a + 1)cm
Then,
p2 + q2 = (a − 1)2 + (2√a)2
= a2 + 1 – 2a + 4a
= a2 + 1 + 2a
= (a + 1)2
r2 = (a + 1)2
p2 + q2 = r2
Thus, the given triangle is right-angled.
2. A man goes 80m due east and then 150m due north. How far is he from the starting point?
Solution
Let the man starts from point A and goes 80 m due east to B.
Then, from B, he goes 150 m due north to c.
We need to find AC.
In right- angled triangle ABC, we have:
AC2 = AB2 + BC2
3. A man goes 10m due south and then 24m due west. How far is he from the starting point?
Solution
Let the man starts from point D and goes 10 m due south at E. He then goes 24 m due west at F.
In right ∆DEF, we have:
DE = 10 m, EF = 24 m
DF2 = EF2 + DE2
Hence, the man is 26 m away from the starting point.
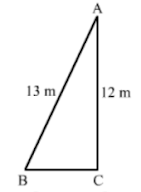
4. A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
Solution
Let AB and AC be the ladder and height of the building.
It is given that:
AB = 13 m and AC = 12 m
We need to find distance of the foot of the ladder from the building, i.e., BC.
In right-angled triangle ABC, we have:
AB2 = AC2 + BC2
Hence, the distance of the foot ladder from the building is 5 m.
5. A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
Solution
Let the height of the window from the ground and the distance of the foot of the ladder from the wall be AB and BC, respectively.
We have:
AB = 20 m and BC = 15 m
Applying Pythagoras theorem in right-angled ABC, we get:
AC2 = AB2 + BC2
Hence, the length of the ladder is 25 m.
6. Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
Solution
Let the two poles be DE and AB and the distance between their bases be BE.
We have:
DE = 9 m, AB = 14 m and BE = 12 m
Draw a line parallel to BE from D, meeting AB at C.
Then, DC = 12 m and AC = 5 m
We need to find AD, the distance between their tops.
Applying Pythagoras theorem in right-angled ACD, we have:
AD2 = AC2 + DC2
⇒ AD2 = 52 + 122 = 25 + 144 = 169
Hence, the distance between the tops to the two poles is 13 m.
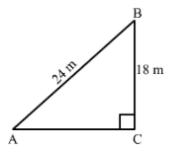
7. A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution
Now, In right triangle ABC
By using Pythagoras theorem, we have
AB2 = BC2 + CA2
⇒ 242 = 182 + CA2
⇒ CA2 = 576 – 324
⇒ CA2 = 252
⇒ CA = 6√7m
Hence, the stake should be driven 6√7m far from the base of the pole.
8. In the given figure, O is a point inside a ∆PQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ∆PQR is right-angled.
Solution
Applying Pythagoras theorem in right-angled triangle POR, we have:
⇒ PR2 = 62 + 82 = 36 + 64 = 100
In ∆ PQR,
PQ2 + PR2 = 242 + 102 = 576 + 100 = 676
And QR2 = 262 = 676
∴ PQ2 + PR2 = QR2
Therefore, by applying Pythagoras theorem, we can say that ∆PQR is right-angled at P.
9. ∆ABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
Solution
It is given that ∆ ABC is an isosceles triangle.
Also, AB = AC = 13 cm
Suppose the altitude from A on BC meets BC at D. Therefore, D is the midpoint of BC.
AD = 5 cm
∆ADB and ∆ADC are right-angled triangles.
Applying Pythagoras theorem, we have;
AB2 = AD2 + BD2
⇒ BD2 = AB2 − AD2 = 132 − 52
⇒ BD2 = 169 − 25 = 144
Hence,
BC = 2(BD) = 2×12 = 24 cm
10. Find the length of altitude AD of an isosceles ∆ABC in which AB = AC = 2a units and BC = a units.
Solution
In isosceles ∆ ABC, we have:
AB = AC = 2a units and BC = a units
Let AD be the altitude drawn from A that meets BC at D.
Then, D is the midpoint of BC.
BD = BC = a/2 units
Applying Pythagoras theorem in right-angled ∆ABD, we have:
⇒ AD2 = AB2 − BD2 = (2a)2 − (a/2)2
⇒ AD2 = 4a2 – a2/4 = 15a2/4
11. ∆ABC is an equilateral triangle of side 2a units. Find each of its altitudes.
Solution
Then, D, E and F are the midpoint of BC, AC and AB, respectively.
In right-angled ∆ABD, we have:
AB = 2a and BD = a
Applying Pythagoras theorem, we get:
AB2 = AD2 + BD2
⇒ AD2 = AB2 − BD2 = (2a)2 − a2
⇒ AD2 = 4a2 − a2 = 3a2
⇒ AD = √3a units
Similarly,
BE = a√3 units and CF = a√3 units
12. Find the height of an equilateral triangle of side 12cm.
Solution
Let ABC be the equilateral triangle with AD as an altitude from A meeting BC at D. Then, D will be the midpoint of BC.
Applying Pythagoras theorem in right-angled triangle ABD, we get:
AB2 = AD2 + BD2
⇒ AD2 = 122 − 62 (∵ BD = 1/2 BC = 6)
⇒ AD2 = 144 − 36 = 108
Hence, the height of the given triangle is 6√3 cm.
13. Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
Solution
Let ABCD be the rectangle with diagonals AC and BD meeting at O.
According to the question:
AB = CD = 30 cm and BC = AD = 16 cm
Applying Pythagoras theorem in right-angled triangle ABC, we get:
AC2 = AB2 + BC2 = 302 + 162 = 900 + 256 = 1156
Diagonals of a rectangle are equal.
Therefore, AC = BD = 34 cm
14. Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Solution
Let ABCD be the rhombus with diagonals (AC = 24 cm and BD = 10 cm) meeting at O. We know that the diagonals of a rhombus bisect each other at angles.
Applying Pythagoras theorem in right-angled AOB, we get:
AB2 = AO2 + BO2 = 122 + 52
⇒ AB2 = 144 + 25 = 169
Solution
In right-angled triangle AED, applying Pythagoras theorem, we have:
AB2 = AE2 + ED2 …(i)
In right-angled triangle AED, applying Pythagoras theorem, we have:
AD2 = AE2+ ED2
⇒ AE2 = AD2 – ED2 ...(ii)
Therefore,
AB2 = AD2 − ED2 + EB2 (from (i) and (ii))
AB2 = AD2 − ED2 + (BD − DE)2
= AD2 − ED2 + (1/2BC − DE)2
= AD2 – DE2 + 1/4 BC2 + DE2 − BC.DE
= AD2 + 1/4BC2 – BC.DE
This completes the proof.
16. In the given figure, ∠ACB = 90° CD ⊥ AB. Prove that BC2/AC2 = BD/AD
Solution
Given: ∠ACB = 90° and CD ⊥ AB
To Prove; BC2/AC2 = BD/AD
Proof: In ∆ ACB and ∆ CDB
∠ACB = ∠CDB = 90° (Given)
∠ABC = ∠CBD (Common)
By AA similarity-criterion ∆ACB ~ ∆CDB
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
∴ BC/BD = AB/BC
⇒ BC2 = BD. AB …(1)
In ∆ ACB and ∆ ADC
∠ACB = ∠ADC = 90° (Given)
∠CAB = ∠DAC (Common)
By AA similarity-criterion ∆ ACB ~ ∆ADC
When two triangles are similar, then the ratios of their corresponding sides are proportional.
∴ AC/AD = AB/AC
⇒ AC2 = AD. AB ...(2)
Dividing (2) by (1), we get
BC2/AC2 = BD/AD
17. In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i) b2 = p2 + ax + a2/x
(ii) c2 = p2 − ax + a2/x
(iii) b2 + c2 = 2p2 + a2/2
(iv) b2 − c2 = 2ax
(i) In right-angled triangle AEC, applying Pythagoras theorem, we have:
AC2 = AE2 + EC2
⇒ b2 = â„Ž2 + (x + a/2)2 = â„Ž2 + x2 + a2/4 + ax …(i)
In right – angled triangle AED, we have:
AD2 = AE2 + ED2
⇒ p2 = h2 + x2 ...(ii)
Therefore,
from (i) and (ii),
b2 = p2 + ax + a2/x
(ii) In right-angled triangle AEB, applying Pythagoras, we have:
AB2 = AE2 + EB2
⇒ c2 = â„Ž2 + (a/2 − x)2 (∵ BD = a/2 and BE = BD - x)
⇒ c2 = h2 + x2 – a2/4 (∵ â„Ž2 + x2 = p2)
⇒ c2 = p2 − ax + a2/x
(iii) Adding (i) and (ii), we get:
⇒ b2 + c2 = p2 + ax + a2/4 + p2 – ax + a2/4
= 2p2 + ax – ax + (a2 + a2)/4
(iv) Subtracting (ii) from (i), we get:
b2 – c2 = p2 + ax + a2/4 – (p2 – ax + a2/4)
= p2 – p2 + ax + ax + a2/4 – a2/4
= 2ax
18. In ∆ABC, AB = AC. Side BC is produced to D. Prove that AD2 − AC2 = BD. CD
Solution
Draw AE ⊥ BC, meeting BC at D.
Applying Pythagoras theorem in right-angled triangle AED, we get:
Since, ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle.
So, BE = CE
And DE + CE = DE + BE = BD
AD2 = AE2 + DE2
⇒ AE2 = AD2 − DE2 …(i)
In ∆ACE,
AC2 = AE2 + EC2
⇒ AE2 = AC2 − EC2 ...(ii)
Using (i) and (ii),
⇒ AD2 – DE2 = AC2 – EC2
⇒ AD2 – AC2 = DE2 – EC2
= (DE + CE) (DE – CE)
= (DE + BE) CD
= BD.CD
19. ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ∆ABE and ∆ACD.
We have, ABC as an isosceles triangle, right angled at B.
Now, AB = BC
Applying Pythagoras theorem in right-angled triangle ABC, we get:
AC2 = AB2 + BC2 = 2AB2 (∵ AB = AC) … (i)
∵ ∆ACD ~ ∆ABE
We know that ratio of areas of 2 similar triangles is equal to squares of the ratio of their corresponding sides.
∴ ar(∆ABE)/ar(∆ACD) = AB2/AC2 [from (i)]
= 1/2
1 : 2
20. An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1.1/2 hours?
Solution
Distance covered by plane A in 1.1/2 hours = 1000 × 3/2 = 1500 km
Distance covered by plane B in 1 1/2 hours = 1200 × 3/2 = 1800 km
Now, In right triangle ABC
By using Pythagoras theorem, we have
AB2 = BC2 + CA2
= (1800)2 + (1500)2
= 3240000 + 2250000
= 5490000
∴ AB2 = 5490000
⇒ AB = 300√61m
Hence, the distance between two planes after 1/1/2 hours 300√61m
21. In a ΔABC, AD is a median and AL ⊥ BC.
(a) AC2 = AD2 + BC.DL + (BC/2)2
(b) AB2 = AD2 – BC.DL + (BC/2)2
(c) AC2 + AB2 = 2AD2 + ½ BC2
Solution
(a) In right triangle ALD
Using Pythagoras theorem, we have
AC2 = AL2 + LC2
= AD2 − DL2 + (DL + DC)2 [Using (1)]
= AD2 − DL2 + (DL + BC/2)2 [∵ AD is a median]
= AD2 − DL2 + DL2 + (BC/2)2 + BC.DL
∴ AC2 = AD2 + BC.DL + (BC/2)2 ...(2)
(b) In right triangle ALD
Using Pythagoras theorem, we have
AL2 = AD2 – DL2 …(3)
Again, In right triangle ABL
Using Pythagoras theorem, we have
AB2 = AL2 + LB2
= AD2 – DL2 + LB2 [Using (3)]
= AD2 – DL2 + (BD – DL)2
= AD2 – DL2 + (1/2 BC – DL)2
= AD2 – DL2 + (BC/2)2 – BC. DL + DL2
∴ AB2 = AD2 – BC. DL + (BC/2)2 ...(4)
(c) Adding (2) and (4), we get,
= AC2 + AB2 = AD2 + BC.DL + (BC/2)2 + AD2 – BC.DL + (BC/2)2
= 2AD2 + BC2/4 + BC2/4
= 2 AD2 + 1/2 BC2
22. Naman is doing fly-fishing in a stream. The trip fishing rod is 1.8m above the surface of the water and the fly at the end of the string rests on the water 3.6m away from him and 2.4 m from the point directly under the tip of the rod. Assuming that the string ( from the tip of his rod to the fly) is taut, how much string does he have out (see the adjoining figure) if he pulls in the string at the rate of 5cm per second, what will be the horizontal distance of the fly from him after 12 seconds?
Hence, after 12 seconds the length of the string he will pulled is given by
12 × 5 = 60 cm or 0.6 m
Now, in ∆BMC
By using Pythagoras theorem, we have
= (2.4)2 + (1.8)2
= 9
∴ BC = 3 m
Now, BC’ = BC – 0.6
= 3 – 0.6
= 2.4 m
Now, In ∆BC’M
By using Pythagoras theorem, we have
C’M2 = BC’2 – MB2
= (2.4)2 − (1.8)2
= 2.52
∴ C’M = 1.6 m
The horizontal distance of the fly from him after 12 seconds is given by
C’A = C’M + MA
= 1.6 + 1.2
= 2.8 m