RS Aggarwal Solutions Chapter 4 Triangles Exercise - 4C Class 10 Maths
Chapter Name | RS Aggarwal Chapter 4 Triangles |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 4C Solutions
1. ∆ABC ~ ∆DEF and their areas are respectively 64 cm2and 121cm2. If EF = 15.4cm, find BC.
Solution
It is given that ∆ABC ~ ∆DEF.
Therefore, ratio of the areas of these triangles will be equal to the ration of squares of their corresponding sides.
ar(∆ABC)/ar(∆DEF) = BC2/EF2
Let BC be X cm.
⇒ 64/121 = x2/(15.4)2
⇒ x2 = (64 × 15.4 × 15.4)/121
⇒ (8 × 15.4)/11
= 11.2
Hence, BC = 11.2 cm
2. The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
Solution
It is given that ∆ABC ~ ∆PQR
Therefore, the ration of the areas of triangles will be equal to the ratio of squares of their corresponding sides.
ar(∆ABC)/ar(∆PQR) = BC2/QR2
⇒ 9/16 = 42/QR2
⇒ QR2 = (4.5 × 4.5 × 16)/9
= (4.5 × 4)/3
= 6 cm
Hence, QR = 6 cm
3. ∆ABC ~ ∆PQR and ar(∆ABC) = 4, ar(∆PQR). If BC = 12cm, find QR.
Solution
Given: (∆ABC) = 4ar(∆PQR)
ar(∆ABC)/ar(∆PQR) = 4/1
∵ ∆ABC ~ ∆PQR
∴ ar(∆ABC)/ar(∆PQR) = BC2/QR2
∴ BC2/QR2 = 4/1
⇒ QR2 = 122/4
⇒ QR2 = 36
⇒ QR = 6 cm
Hence, QR = 6 cm
4. The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
Solution
It is given that the triangles are similar.
Therefore, the ratio of the areas of these triangles will be equal to the ratio of squares of their corresponding sides.
Let the longest side of smaller triangle be X cm.
ar(Larger triangle)/ar(Smaller triangle) = (Longest side of larger triangle)2/(Longest side of smaller triangle)2
⇒ 169/121 = 262/x2
= 22
Hence, the longest side of the smaller triangle is 22 cm.
5. ∆ABC ~ ∆DEF and their areas are respectively 100 cm2 and 49cm2. If the altitude of ∆ABC is 5cm, find the corresponding altitude of ∆DEF.
Solution
It is given that ∆ABC ~ ∆DEF.Therefore, the ration of the areas of these triangles will be equal to the ratio of squares of their corresponding sides.
Also, the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Let the altitude of ∆ABC be AP, drawn from A to BC to meet BC at P and the altitude of ∆DEF be DQ, drawn from D to meet EF at Q.
Then,
ar(∆ABC)/ar(∆DEF) = AP2/DQ2
⇒ 100/49 = 52/DQ2
⇒ 100/49 = 25/DQ2
⇒ DQ2 = (49 × 25)/100
⇒ DQ = 3.5 cm
Hence, the altitude of ∆DEF is 3.5 cm
6. The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
Solution
Let the two triangles be ABC and DEF with altitudes AP and DQ, respectively.
It is given that ∆ ABC ~ ∆ DEF.
We know that the ration of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
∴ ar(∆ABC)/ar(∆DEF) = (AP)2/(DQ)2
⇒ ar(∆ABC)/ar(∆DEF) = 62/92
= 36/81
= 4/9
Hence, the ratio of their areas is 4 : 9
7. The areas of two similar triangles are 81cm2 and 49cm2 respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
Solution
It is given that the triangles are similar.
Therefore, the areas of these triangles will be equal to the ratio of squares of their corresponding sides.
Also, the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Let the two triangles be ABC and DEF with altitudes AP and DQ, respectively.
⇒ 81/49 = 6.32/DQ
⇒ DQ2 = 49/81 × 6.32
Hence, the altitude of the other triangle is 4.9 cm.
8. The areas of two similar triangles are 64cm2 and 100cm2 respectively. If a median of the smaller triangle is 5.6cm, find the corresponding median of the other.
Solution
Let the two triangles be ABC and PQR with medians AM and PN, respectively.
Therefore, the ratio of areas of two similar triangles will be equal to the ratio of squares of their corresponding medians.
∴ ar(∆ABC)/ar(∆PQR) = AM2/PN2
⇒ 64/100 = 5.62/PN2
⇒ PN2 = (64/100 × 5.62)
= 7 cm
Hence, the median of the larger triangle is 7 cm.
9. In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1cm, PB = 3 cm, AQ = 1.5cm, QC = 4.5cm, prove that area of ∆APQ is 1/16 of the area of ∆ABC.
SolutionWe have:
AP/AB = 1/(1 + 3) = 1/4 and AQ/AC = 1.5/(1.5 + 4.5) = 1.5/6 = 1/4
⇒ AP/AB = AQ/AC
Also, ∠A = ∠A
By SAS similarity, we can conclude that ∆APQ - ∆ABC.
ar(∆APQ)/ar(∆ABC) = AP2/AB2 = 12/42 = 1/16
⇒ ar(∆APQ)/ar(∆ABC) = 1/16
⇒ ar(∆APQ) = 1/16 × ar (∆ABC)
Hence proved.
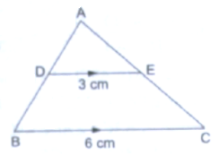
10. In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(∆ADE) = 15cm2, find the area of ∆ABC.
SolutionIt is given that DE || BC
∴ ∠ADE = ∠ABC (Corresponding angles)
∠AED = ∠ACB (Corresponding angles)
By AA similarity, we can conclude that ∆ADE ~ ∆ABC
∴ ar(∆ADE)/ar(∆ABC) = DE2/BC2
⇒ 15/ar(∆ABC) = 32/62
⇒ ar(∆ABC) = 32/62
⇒ ar(∆ABC) = (15 × 36)/9
= 60 cm2
Hence, area of triangle ABC is 60 cm2.
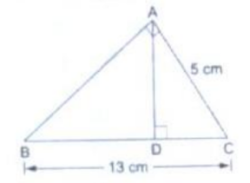
11. ∆ABC is right angled at A and AD⊥BC. If BC = 13cm and AC = 5cm, find the ratio of the areas of ∆ABC and ∆ADC.
SolutionIn ∆ABC and ∆ADC, we have:
∠BAC = ∠ADC = 90°
∠ACB = ∠ACD (common)
By AA similarity, we can conclude that ∆BAC~ ∆ADC.
Hence, the ratio of the areas of these triangles is equal to the ratio of squares of their corresponding sides.
∴ ar(∆BAC)/ar(∆ADC) = BC2/AC2
⇒ ar(∆BAC)/ar(∆ADC) = 132/52
= 169/25
Hence, the ratio of areas of both the triangles is 169:25
12. In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED.
SolutionIt is given that DE || BC.
∴ ∠ADE = ∠ABC (Corresponding angles)
∠AED = ∠ACB (Corresponding angles)
Applying AA similarity theorem, we can conclude that ∆ ADE ~ ∆ABC.
∴ ar(∆ABC)/ar(∆ADE) = BC2/DE2
Subtracting 1 from both sides, we get:
ar(∆ABC)/ar(∆ADE) – 1 = 52/32 - 1
⇒ (ar(∆ABC) - ar(∆ADE)/ar(∆ADE) = (25 – 9)/9
⇒ ar(BCED)/ar(∆ADE) = 16/9
Or, ar(∆ADE)/ar(BCED) = 9/16
13. In ∆ABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ∆ADE and ∆ABC.
SolutionIt is given that D and E are midpoints of AB and AC.
Applying midpoint theorem, we can conclude that DE ‖ BC.
Hence, by B.P.T., we get:
AD/AB = AE/AC
Also, ∠A = ∠A
Applying SAS similarity theorem, we can conclude that ∆ ADE~ ∆ ABC.
Therefore, the ration of areas of these triangles will be equal to the ratio of squares of their corresponding sides.
∴ ar(∆ADE)/ar(∆ABC) = DE2/BC2
= (1/2 BC)2/BC2
= 1/4