Chapter 9 Quadrilaterals NCERT Solutions Class 9 Maths

NCERT Solutions for Chapter 8 Quadrilaterals Class 9 Maths

Chapter Name	NCERT Solutions for Chapter 8 Quadrilaterals
Class	Class 9
Topics Covered	About Quadrilaterals Properties of Angles of Quadrilaterals Types of Quadrilaterals Properties of Parallelograms Properties of Rectangle and Square Properties of Rhombus
Related Study Materials	NCERT Solutions for Class 9 Maths NCERT Solutions for Class 9 Revision Notes for Chapter 8 Quadrilaterals Class 9 Maths Important Questions for Chapter 8 Quadrilaterals Class 9 Maths MCQ for for Chapter 8 Quadrilaterals Class 9 Maths

Short Revision for Ch 8 Quadrilaterals Class 9 Maths

1. There are four sides of a quadrilateral.
2. The sum of the angles of a quadrilateral is 360°. This property is called Angle Sum Property of a Quadrilateral.
3. Types of quadrilaterals: Trapezium, parallelogram, rectangle, rhombus, square.
4. One pair of opposite sides of a trapezium is parallel.
5. Properties of parallelogram:
   (i) Opposite sides are equal and parallel.
   (ii) Opposite angles are equal.
   (iii) Diagonals bisect each other.
   (iv) Each of diagonals divides the parallelogram into two congruent triangles.
6. Properties of a rectangle:
   (i) Opposite sides are equal and parallel.
   (ii) Each of angles is of 90°.
   (iii) Diagonals are of equal lengths.
   (iv) Diagonals bisect each other.
   (v) Each of diagonals divides the rectangle into two congruent triangles.
7. A kite is not a parallelogram.
8. Properties of a rhombus:
   (i) All the sides are of equal lengths.
   (ii) Opposite angles are equal.
   (iii) Diagonals bisect each other at right angles.
   (iv) Each diagonal divides the rhombus into two congruent triangles. 
9. Properties of a square :
   (i) All the sides are of equal lengths.
   (ii) Each of angle is of 90°.
   (iii) Diagonals are of equal lengths.
   (iv) Diagonals bisect each other at right angles.
   (v) Each diagonal divides the square into 
10. A parallelogram is a trapezium. 
11. A square is a rectangle as well as a rhombus. 
12. The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and half of it. 

Exercise 8.1 

1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.

2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.

3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

4. Show that the diagonals of a square are equal and bisect each other at right angles.

5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

6. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig.) Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.

7. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.

9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.) Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram

10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig) Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ

11. In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig.)
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.

12. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
[Hint : Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

Exercise 8.2

1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29). AC is a diagonal. Show that:

(i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

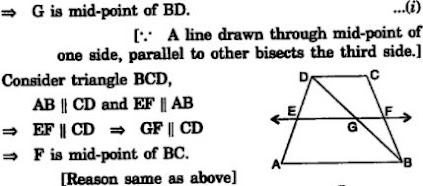
4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.

Solution

Consider △ADB, AB॥EF

⇒ AB॥ EG. 

5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.

6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other. 

Solution

(i) Consider triangle ACD, 

7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½ AB