Chapter 7 Triangles NCERT Solutions Class 9 Maths

NCERT Solutions for Chapter 7 Tringles Class 9 Maths

Chapter Name	NCERT Solutions for Chapter 7 Triangles
Class	Class 9
Topics Covered	Congruent Figures Congruency of Triangles Congruency criterion
Related Study Materials	NCERT Solutions for Class 9 Maths NCERT Solutions for Class 9 Revision Notes for Chapter 7 Triangles Class 9 Maths Important Questions for Chapter 7 Triangles Class 9 Maths MCQ for for Chapter 7 Triangles Class 9 Maths

Short Revision for Ch 7 Triangles Class 9 Maths

1. Congruent figures are of same size and same shape.
2. When placing a figure of two congruent figures on the other one, they cover each other completely.
3. Two circles of the same radii are congruent.
4. Two squares of the same sides are congruent.
5. Two photographs of same sizes but different pictures are not congruent.
6. Types of triangles: Equilateral, isosceles, acute-angled, obtuse-angled, right-angle, scalene triangles.
7. If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent (SSS congruence rule).
8. If two sides and the included angle of one triangle are equal to the two sides and included angle of another triangle, then the two triangles are congruent (SAS congruence rule).
9. If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent (ASA congruence rule).
10. If two angles and one side (other than included side) of one triangle are equal to two angles and one side (other than included side) of another triangle, then the two triangles are congruent (AAS congruence rule). 
11. In two right - angled triangles, if hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent (RHS congruence rule). 
12. Sum of angles of a triangle is 180° . This property is called Angle Sum Property of a Triangle. 
13. A triangle in which all the three sides are equal is called an equilateral triangle.
14. All the three angles of an equilateral triangle are equal, measuring 60° each.
15. A triangle in which two sides are equal is called an isosceles triangle.
16. Angles opposite to equal sides of a triangle are equal.
17. Sides opposite to equal angles of a triangle are equal.
18. The angle opposite to longer side of a triangle is larger.
19. The side opposite to the larger angle of a triangle is longer.
20. The sum of the two sides of a triangle is greater than the third side.
21. The difference of the two sides of a triangle is less than the third side.
22. All the three sides of a scalene triangle are of different lengths. 

Exercise 7.1 

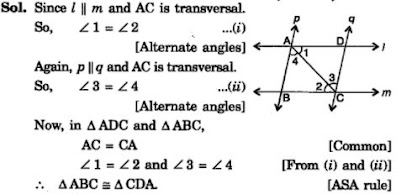
1. In quadrilateral ACBD, AC = AD and AB bisect ∠A see Fig. Show that ΔABC ΔABD. What can you say about BC and BD?

2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA see Fig. Prove that
(i) ΔABD ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

Solution

(i) Consider triangles ABD and ABC, 

3. AD and BC are equal perpendiculars to a line segment AB see Fig.  Show that CD bisects AB.

4. l and m are two parallel lines intersected by another pair of parallel lines p and q see Fig.  Show that ΔABC ≅ ΔCDA.

5. Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A see Fig. Show that:
(i) ΔAPB ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

6. In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB see Fig.  Show that
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE.

8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B see Fig.  Show that:
(i) ΔAMC ≅ ΔBMD
(ii) ∠DBC is a right angle.
(iii) ΔDBC ≅ ΔACB
(iv) CM = ½ AB

Exercise 7.2 

1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A. 

2. In ΔABC, AD is the perpendicular bisector of BC see Fig.  Show that ΔABC is an isosceles triangle in which AB = AC.

3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively see Fig.  Show that these altitudes are equal.

4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal see Fig.  Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle. 

5. ABC and DBC are two isosceles triangles on the same base BC see Fig.  Show that ∠ABD = ∠ACD.

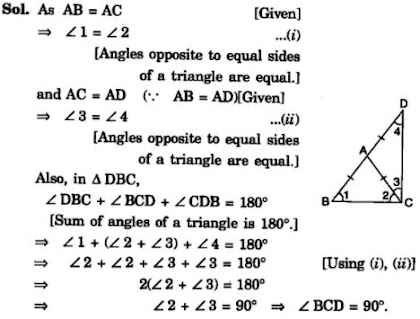
6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB see Fig.  Show that ∠BCD is a right angle.

7. ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

8. Show that the angles of an equilateral triangle are 60° each.

Exercise: 7.3 

1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC see Fig. If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.

2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects A.

3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR

4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

Exercise 7.4 

1. Show that in a right-angled triangle, the hypotenuse is the longest side.

2. In Fig. sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

3. In Fig. ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD see Fig.
Show that ∠A  > ∠C and ∠B > ∠D.

5. In Fig  PR > PQ and PS bisect ∠QPR. Prove that ∠PSR > ∠PSQ.

6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Exercise 7.5 

1. ABC is a triangle. Locate a point in the interior of △ABC which is equidistant from all the vertices of △ABC.

Sol. We know that any point on the perpendicular bisector of the line segment is equidistant from the end points of the line segment. 
Hence, 
(i) Draw the perpendicular bisector of line segment BC. 
(ii) Draw the perpendicular bisector of line segment AC. 
Let these perpendicular bisectors meet at O. 
Then we have OB = OC = OA, i.e., O is a point equidistant from the vertices of a triangle ABC .

2. In a triangle locate a point in its interior which is equidistant from all the sides of the triangle. 

3. In a huge park, people are concentrated at three points (see  figure) : 
A. where there are different slides and swings for children. 
B. near which a man - made lake is situated. 
C. which is near to a large parking and exit. 
Where should an ice cream parlour be set up so that maximum number of persons can approach it?

[Hint: The parlour should be equidistant from A, B and C.]

Solution

Position should be equidistant from A, B and C. 
We know that any point on the perpendicular bisector of the line segment is equidistant from the end points of the line segment. Hence, 

4. Complete the hexagonal and star shaped Rangolies [see figure (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ?