ICSE Solutions for Selina Concise Chapter 17 Circle Class 9 Maths
Exercise 17(A)
1. A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the center of the circle.Let AB be the chord and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.
We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
AC = CB = 3 cm
In △OCA,
OA2 = OC2 + AC2 (By Pythagoras theorem)
⇒ OC2 = (5)2 – (3)2 = 15
⇒ OC = 4 cm
Let AB be the chord and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
∴ AB = 8cm
⇒ AC = OB = AB/2
⇒ AC = OB = 8/2
⇒ AC = OB = 4cm
In △OCA,
OA2 = OC2 + AC2 (By Pythagoras theorem)
⇒ OA2 = (4)2 + (3)2 = 25
⇒ OA= 5 cm
Hence, radius of the circle is 5 cm.
Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord
∴ AC = CB
In △OCA,
OA2 = OC2 + AC2 (By Pythagoras theorem)
⇒ AC2 = (17)2 – (8)2 = 225
⇒ AC= 15 cm
∴ AB = 2AC = 2×15 = 30 cm.
Let AB be the chord of length 24 cm and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.
We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
AC = CB = 12 cm
In △OCA,
OA2 = OC2 + AC2 (By Pythagoras theorem)
⇒ OA2 = (5)2 + (12)2 = 169
⇒ OA= 13 cm
∴ radius of the circle = 13cm.
Let A 'B' be the new chord at a distance of 12cm from the centre.
∴ (OA')2 = (OC')2 + (A'C')2 (By Pythagoras theorem)
⇒ (A'C')2 = (13)2 – (12)2 = 25
∴ A'C'= 5 cm
Hence, length of the new chord = 2×5 = 10cm.
We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.
∴ BP = PC
By Pythagoras Theorem,
OB2 = OP2 + BP2 (By Pythagoras theorem)
⇒ BP2 = (20)2 – (16)2 = 144
∴ BP= 12 cm
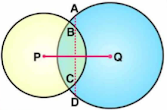
For the outer circle, AD is the chord and OP ⊥ AD.
We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.
AP = PD
By Pythagoras Theorem,
OA2 = OP2 + AP2
⇒ AP2 = (34)2 – (16)2 = 900
⇒ AP = 30 cm
⇒ AB = AP – BP = 30 – 12 = 18 cm
(i) on the opposite sides of the centre;
(ii) on the same side of the centre.
AnswerLet O be the centre of the circle and AB and CD be the two parallel chords of length 30 cm and 16 cm respectively.
Drop OE and OF perpendicular on AB and CD from the centre O.

OE⟂AB and OF ⟂ CD
∴ OE bisects AB and OF bisects CD
[Perpendicular drawn from the centre of a circle to a chord bisects it]
⇒ AE = 30/2 = 15cm ; CF = 16/2 = 8cm
In right △OAE,
OA2 = OE2 + AE2 (By Pythagoras theorem)
⇒ OE2 = OA2 - AE2 = (17)2 - (15)2 = 64
⇒ OF2 = OC2 - CF2 = (17)2 - (8)2 = 225
(i) The chords are on the opposite sides of the centre :
∴EF = EO + OF = (8+15) = 23cm
(ii) The chords are on the same side of the centre :
∴ EF = OF - OE = (15 - 8) = 7cm
Since the distance between the chords is greater than the radius of the circle (15 cm), so the chords will be on the opposite sides of the centre.
Let O be the centre of the circle and AB and CD be the two chords such that AB = 24cm.Let length of CD be 2x cm.
Drop OE and OF perpendicular on AB and CD from the centre O.
OE ⟂ AB and OF⟂CD
∴ OE bisects AB and OF bisects CD
[perpendicular drawn from the centre of a circle to a chord bisects it]
⇒ AE = 24/2 = 12cm ; CF = 2x/2 = x cm
In right △OAE,
⇒ OE2 = OA2 - AE2 = (15)2 - (12)2 = 81
∴ OF = EF - OE = (21 - 9) = 12cm
In right △OCF,
⇒ x2 = OC2 - OF2 = (15)2 - (12)2 = 81
Hence, length of chord CD = 2x = 2×9 = 18cm
8. A chord CD of a circle whose centre is O, is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm. Calculate the lengths of:
(i) CD ; (ii) AD ; (iii) CB.
Answer
(i) OP ⟂ CD
∴ OP bisects CD
[Perpendicular drawn from the centre of a circle to a chord bisects it]
⇒ CP = CD/2
In right △OPC,
⇒ CP2 = OC2 - OP2 = (15)2 - (9)2 = 144
(ii) Join BD,
∴ BP = OB - OP = 15 - 9 = 6cm
In right △BPD,
BD2 = BP2 + PD2 = (6)2 + (12)2 = 180
In △ADB,
∴ AB2 = AD2 + BD2
(iii) Also, BC = BD = √180 = 13.42cm

Let the radius of the circle be r cm.
∴ OE = OB - EB = r - 4
Join OC,
In right △OEC ,
∴ OC2 = OE2 + CE2
⇒ 8r = 80
∴ r = 10 cm
Hence, radius of the circles is 10 cm.
10. In the given figure, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm, Find the:
(i) radius of the circle
(ii) length of chord CD
Answer(i) AB is the chord of the circle and OM is perpendicular to AB.
So, AM = MB = 12cm (Since ⟂ bisects the chord)
In right △OMA,
OA2 = OM2 + AM2
⇒ OA2 = 52 + 122
⇒ OA = 13cm
So, radius of the circle is 13cm.
(ii) So, OA = OC = 13cm (radii of the same circle)
In right △ONC,
NC2 = OC2- ON2
⇒ NC2 = 132 - 122
⇒ NC = 5cm
So, CD = 2NC = 10cm
Exercise 17(B)
1. The figure shows two concentric circles and AD is a chord of larger circle. Prove that: AB = CD.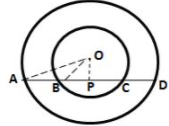
Drop OP ⟂ AD
∴ OP bisects AD
[Perpendicular draw from the centre of a circle to a chord bisects it]
⇒ AP = PD ...(i)
Now,
∴ OP bisects BC
[Perpendicular drawn from the centre of a circle to a chord bisects it]
⇒ BP = PC ...(ii)
Subtracting (ii) from (i),
AP - BP = PD - PC
⇒ AB = CD
2. A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.

Given: A straight line Ad intersects two circles of equal at A, B, C and D.
The line joining the centres OO' intersect AD at M and M is the midpoint of OO'.
To prove: AB = CD.
Construction: From O, draw OP ⊥ AB and from O', draw O'Q ⊥ CD .
Proof :
In △OMP and △O'MQ,
∠OMP = ∠O'MQ (Vertically opposite angles)
∠OPM = ∠O'QM (each = 90°)
OM = O'M (Given)
By Angle - Angle - Side criterion of congruence,
∴ △OMP ≅ △O'MQ (by AAS)
The corresponding parts of the congruent triangles are congruent
∴ OP = O'Q (c.p.c.t)
we know that two chords of a circle or equal circles which are equidistant from the centre are equal.
∴ AB = CD
(i) ∠BMN = ∠DNM,
(ii) ∠AMN = ∠CNM.
Answer
Drop OM ⊥ AB and ON ⊥ CD
∴ OM bisects AB and ON bisects CD.
[Perpendicular drawn from the centre of a circle to a chord bisects it]
⇒ BM = (1/2)AB = (1/2)CD = DN ...(1)
Applying Pythagoras theorem,
∴ OM = ON
⇒ ∠OMN = ∠ONM ...(2) (Angles opp. to equal sides are equal)
(i) ∠OMB = ∠OND (both 90°)
Subtracting (2) from above,
∠BMN = ∠DNM
(ii) ∠OMA = ∠ONC (both 90°)
Adding(2) to above,
∠AMN = ∠CNM
(i) OO' = (1/2)AB
(ii) AB = CD
AnswerDrop OM and O’N perpendicular on AB and OM’ and O’N’ perpendicular on CD.

OM, O'N, OM' and O'N' bisect AP, PB, CQ and QD respectively
[Perpendicular drawn from the centre of a circle to a chord bisects it]
∴ MP = (1/2)AP, PN = (1/2)BP, M'Q = (1/2)CQ, ON' = (1/2)QD
Now,
and, OO' = M'N' = M'Q + QN' = (1/2)(CQ + QD) = (1/2)CD ...(ii)
By (i) and (ii),
AB = CD
(i) AP = CP
(ii) BP = DP
Drop OM and ON perpendicular on AB and CD.
Join OP, OB and OD.

∴ OM and ON bisects AB and CD respectively
[Perpendicular drawn from the centre of a circle to a chord bisects it)
∴ MB = (1/2)AB = (1/2)CD = ND ...(i)
In right △OMB,
In right △OND,
From (i), (ii) and (iii)
OM = ON
In △OPM and △OPN,
∠OMP = ∠ONP (both 90°)
OP = OP (common)
OM = ON (Proved above)
By Right Angle - Hypotenuse - Side criterion of congruence,
∴ △OPM ≅ △OPN (by RHS)
The corresponding parts of the congruent triangles are congruer
∴ PM = PN (c.p.c.t)
Adding (i) to both sides,
MB + PM = ND + PN
⇒ BP + DP
Now, AB = CD
∴ AB - BP = CD - DP (∵ BP = DP)
⇒ AP = CP
(i) △OPA ≅ △OQC,
(ii) △BPC ≅ △BQA.

(i) In △OPA and △OQC,
OP = OQ (radii of same circle)
∠AOP = ∠COQ (both 90°)
OA = OC (sides of the square)
By Side - Angle - Side criterion of congruence,
∴ △OPA ≅ △OQC (by SAS)
(ii) Now, OP = OQ (radii)
and OC = OA (sides of the square)
∴ OC - OP = OA - OQ
⇒ CP = AQ ...(1)
In △BPC and △BQA,
BC = BA (sides of the square)
PC = QA [by (1)]
By Side - Angle - Side criterion of congruence,
∴ △BPC ≅ △BQA (by SAS)
7. The length of the common chord of two intersecting circles is 30 cm. If the diameters of these two circles be 50 cm and 34 cm, calculate the distance between their centres.

OA = 25cm and AB = 30cm
∴ AD = (1/2)×AB = (1/2)×30 cm = 15cm
Now, in right angled △ADO,
OA2 = AD2 + OD2
⇒ OD2 = OA2 - OD2 = 252 - 152
⇒ OD2 = 625 - 225 = 400
∴ OD = √400 = 20cm
Again we have,
In right angle △ADO'
O'A2 = AD2 + O'D2
= 289 - 225 = 64
∴ O'D= 8cm
∴ OO' = (OD + O'D)
⇒ OO' = (20+ 8) = 28 cm
8. The line joining the midpoints of two chords of a circle passes through its centre. Prove that the chords are parallel.
Answer
Given: AB and CD are the two chords of a circle with centre O.
L and M are the midpoints of AB and CD and O lies in the line joining ML.
To prove: AB ॥CD.
Proof: AB and CD are two chords of a circle with centre O. Line LOM bisects them at L and M
Then, OL ⊥ AB
and, OM ⊥ CD
∴ ∠ALM = ∠LMD = 90°
But they are alternate angles
∴ AB ॥ CD.
9. In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of the circles. Show that:
(i) AB = CD ;
(ii) AC = BD.
Answer∴ OA = OD ...(1)
[Perpendicular drawn from the centre of a circle to a chord bisects it]
In the circle with centre P, PO ⊥ BC
∴ OB = OC ...(2)
[Perpendicular drawn from the centre of a circle to a chord bisects it]
(i) (1) - (2) gives,
AB = CD ...(3)
(ii) Adding BC to both sides of equation (3)
AB + BC = CD + BC
⇒ AC = BD
OM ⊥ AB and ON⊥CD
∴ BM = (1/2)AB = (1/2)CD = CN ...(i)
[Perpendicular drawn from the centre of a circle to a chord bisects it]
As the two equal chords AB and CD intersects at point P inside the circle,
∴ AP = DP and CP = BP ...(ii)
Now, CN - CP = BM - BP [by (i) and (ii)]
⇒ PN = MP
∴ Quadrilateral OMPN is a square.
Exercise 17(C)
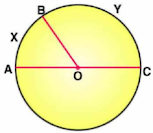
1. In the given figure, an equilateral triangle ABC is inscribed in a circle with centre O.Find:
(i) ∠BOC
(ii) ∠OBC
In the given figure, ABC is an equilateral triangle.
Hence, all the three angles of the triangle will be equal to 60°
i.e. ∠A = ∠B = ∠C = 60°
As the triangle is an equilateral triangle, BO and CO will be the angle bisectors of B and C respectively.
Hence,
∠OBC = ∠ABC/2 = 30°
and as given in the figure we can see that OB and OC are the radii of the given circle.
Hence they are of equal length.
The ΔOBC is an isosceles triangle with OB = OC
In ΔOBC,
∠OBC = ∠OCB as they are angles opposite to the two equal sides of an isosceles triangle.
Hence,
∠OBC = 30° and ∠OCB = 30°
Since, the sum of all angles of a triangle is 180°
Hence, in triangle OBC,
∠OCB + ∠OBC + ∠BOC + BOC = 180°
⇒ 30° + 30° + ∠BOC= 180°
⇒ 60° + BOC = 180°
⇒ ∠BOC = 180° – 60°
⇒ ∠BOC = 120°
Hence, ∠BOC =120° and ∠OBC =30°
(i) ∠BOC
(ii) ∠OCB
(iii) ∠COD
(iv) ∠BOD
Is BD a diameter of the circle?
AnswerIn the given figure we can extend the straight line OB to BD and CO to CA
Then we get the diagonals of the square which intersect each other at 90 by the property of Square.
From the above statement, we can see that
∠COD = 90°
The sum of the angle ∠BOC and ∠COD is 180° as BD is a straight line.
Hence, ∠BOC + ∠OCD = ∠BOD = 180°
⇒ ∠BOC + 90° = 180°
⇒ ∠BOC + 180° – 90°
⇒ ∠BOC = 90°
We can see that the OCB is an isosceles triangle with sides OB and OC of equal length as they are the radii of the same are.
In ΔOCB,
∠OBC = ∠OCB as they are opposite angles to the two equal sides of an isosceles triangle.
Sum of all the angles of a triangle is 180°
so, ∠OBC + ∠OCB + ∠BOC =180°
⇒ ∠OBC + ∠OBC + 90° = 180° (∠OBC = ∠OCB)
⇒ 2∠OBC = 180° – 90°
⇒ 2∠OBC = 90°
⇒ 2∠OBC = 45° (∠OBC = ∠OCB)
So, ∠OBC = OCB = 45°
Yes, BD is the diameter of the order.
(i) ∠AOB
(ii) ∠BOC
(iii) ∠AOC
(iv) ∠OBA
(v) ∠OBC
(vi) ∠ABC
AnswerAs given that AB is the side of a pentagon the angle subtended by each arm of the pentagon at the center of the circle is = 360°/5 = 72°
Thus angle ∠AOB = 72°
Similarly, as BC is the side of a hexagon hence the angle subtended by BC at the center is = 360°/6 i.e. 60°
∠BOC = 60°
Now, ∠AOC = ∠AOB + ∠BOC =72° + 60° = 132°
The triangle thus formed, AOB is an isosceles triangle with OA = OB as they are radii of the same circle.
Thus ∠OBA = ∠BAO as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
so, ∠AOB + ∠OBA + ∠BAO = 180°
⇒ 2∠OBA + 72° = 180° (∠OBA = ∠BAO)
⇒ 2∠OBA = 180° – 72°
⇒ 2∠OBA = 180°
⇒ 2∠OBA =54° (∠OBA = ∠BAO)
So, ∠OBA = ∠BAO = 54°
The triangle thus formed, ΔBOC is an isosceles triangle
with OB = OC as they are radii of the same are.
Thus ∠OBC = ∠OCB as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
so, ∠BOC + ∠OBC + ∠OCB = 180°
⇒ 2∠OBC + 60° = 180° (∠OBC = ∠OCB)
⇒ 2∠OBC = 180° – 60°
⇒ 2∠OBC = 120°
⇒ ∠OBC = 60° (∠OBC = ∠OCB)
So, ∠OBC = ∠OCB
⇒ ∠ABC = ∠OBA + ∠OBC = 54° + 60°= 144°
(i) ∠BOC
(ii) ∠OBC
(iii) ∠AOC
(iv) ∠OAC
We know that the arc of equal lengths subtends equal angles at the center.
Hence,
∠AOB = ∠BOC = 48°
Then, ∠AOC = ∠AOB + ∠BOC = 48° + 48° = 96°
The triangle thus formed, ΔBOC is an isosceles triangle with OB = OC as they are radii of the same circle.
Thus, ∠OBC = ∠OCB as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
So, ∠BOC + ∠OBC + ∠OCB = 180°
⇒ 2∠OBC + 48° = 180° (∠OBC = ∠OCB)
⇒ 2∠OBC = 180° – 48°
⇒ 2∠OBC = 132°
⇒ ∠OBC = 66° (∠OBC = ∠OCB)
So, ∠OBC = ∠OCB = 66°
The triangle thus formed, ΔAOC is an isosceles triangle with OA = OC as they are radii of the same circle.
Thus ∠OAC = ∠OCA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
So, ∠COA + ∠OAC + ∠OCA = 180°
⇒ 2∠OAC + 96° = 180° (∠OAC = ∠OCA)
⇒ 2∠OAC = 180° – 96°
⇒ 2∠OAC = 84°
⇒ ∠OAC = 42° (∠OCA = ∠OAC)
So, ∠OCA = ∠OAC = 42°.
If ∠AOB = 96°, find:
(i) ∠BOC
(ii) ∠ABC
AnswerWe know that for two arcs are in ratio 3: 2 then
∠AOB: ∠BOC = 3: 2
As give ∠AOC = 96°
So, 3x = 96
⇒ x = 32
There, ∠BOC = 2×32 = 64°
The triangle thus formed, ΔAOB is an isosceles triangle with OA = OB as they are radii of the same circle.
Thus ∠OBA = ∠BAO as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠AOB + ∠OBA + ∠BAO = 180°
⇒ 2∠OBA + 96° = 180° (∠OBA = ∠BAO)
⇒ 2∠OBA = 180° – 96°
⇒ 2∠OBA = 84°
⇒ ∠OBA = 42° (∠OBA = ∠BAO)
So, ∠OBA = ∠BAO = 42°
The triangle thus formed, ΔBOC is an isosceles triangle with OB = OC as they are radii of the same circle.
Thus ∠OBC = ∠OCB as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠BOC + ∠OBC + ∠OCB = 180°
2∠OBC + 64° = 180° (∠OBC = ∠OCB)
2∠OBC = 180° – 64°
2∠OBC = 116°
∠OBC = 58° (∠OBC = ∠OCB)
So, ∠OBC = ∠OCB = 58°
⇒ ∠ABC = ∠BOA + ∠OBC = 42°+ 58° = 100°
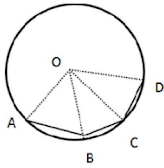
(i) ∠AOC
(ii) ∠AOD
(iii) ∠BOD
(iv) ∠OAC
(v) ∠ODA
AnswerSo, ∠AOB = ∠BOC = 50°
Now,
∠AOC = ∠AOB + ∠BOC = 50° + 50° = 100°
As arc AB, arc BC and arc CD so,
∠AOB = ∠BOC = ∠COD = 50°
⇒ ∠AOD = ∠AOB + ∠BOC + ∠COD = 50° + 50° + 50° = 150°
Now, ∠BOD = ∠BOC + ∠COD
⇒ ∠BOD = 50° + 50°
⇒ ∠BOD = 100°
The triangle thus formed, ΔAOC is an isosceles triangle with OA = OC as they are radii of the same circle.
Thus ∠OAC = ∠OCA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠AOC + ∠OAC + ∠OCA = 180°
⇒ 2∠OAC + 100° = 180° as, ∠OAC = ∠OCA
⇒ 2∠OAC = 180° – 100°
⇒ 2∠OAC = 80°
⇒ ∠OAC = 40°
as ∠OCA = ∠OAC
So, ∠OCA = ∠OAC = 40°
The triangle thus formed, ΔAOD is an isosceles triangle with OA = OD as they are radii of the same circle.
Thus, ∠OAD = ∠ODA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠AOD + ∠OAD + ∠ODA = 180°
⇒ 2∠OAD + 150° = 180° as, ∠OAD = ∠ODA
⇒ 2∠OAD = 180° – 150°
⇒ ∠OAD = 30°
as ∠OAD = ∠ODA So,
⇒ ∠OAD = ∠ODA = 15°.
(i) ∠AOB
(ii) ∠AOC
(iii) ∠BOC
(iv) ∠OBC
Answer
As AB is the side of a hexagon so the
∠AOB = 360°/6 = 60°
AC is the side of an eight sided polygon so,
∠AOC = 360°/8 = 45°
From the given figure we can see that:
∠BOC = ∠AOB + ∠AOC = 60° + 45° = 105°
Again, from the figure we can see that △BOC is an isosceles triangle with sides BO = OC as they are the radii of the same circle.
Angles ∠OBC = ∠OCB as they are opposite angles to the equal sides of an isosceles triangle.
Sum of all the angles of a triangle is 180°
∠OBC+∠OCB + ∠BOC = 180°
⇒ 2∠OBC + 105° = 180° (∠OBC = ∠BOC)
⇒ 2∠OBC = 180° - 105°
⇒ 2∠OBC = 75°
⇒ ∠OBC = 37.5° = 37°30'
As, ∠OBC = ∠BOC
⇒ ∠OBC = ∠BOC = 37.5° = 37°30'
8. In the given figure, O is the center of the circle and the length of arc AB is twice the length of arc BC. If ∠AOB = 100°,
find: (i) ∠BOC (ii) ∠OAC
We know that when two arcs are in ratio 2: 1 then the subtended by them is also in ratio 2: 1
As given arc AB is twice the length of arc BC.
Therefore, arc AB: arc BC = 2: 1
Hence, ∠AOB: ∠BOC = 2: 1
Now given that ∠AOB = 100°.
So, ∠BOC = 1/2∠AOB=1/2×100°=50°
Now, ∠AOC = ∠AOB + ∠BOC = 100° + 50° = 150°.
The triangle thus formed, ∠AOC is an isosceles triangle with OA = OC as they are radii of the same circle.
Thus,
∠OAC = ∠OCA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
So, ∠COA + ∠OAC + ∠OCA = 180°
⇒ 2∠OAC + 150° = 180° as, ∠OAC = ∠OCA
⇒ 2∠OAC = 180° – 150°
⇒ 2∠OAC = 30°
⇒ ∠OAC = 15°
as ∠OCA = ∠OAC So,
⇒ ∠OCA = ∠OAC = 15°.
Exercise 17(D)
1. The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centre.⇒ OM2 = OA2 - AM2
⇒ OM = 5cm
Hence, the distance of the chord from the centre is 5 cm.

Given: AB and CD are two equal chord of congruent circles with centres O and O' respectively.
To prove: ∠AOB = ∠OO'D
Proof: In △OAB and △O'CD,
OA = O'C (∵ Radii of congruent circles)
OB = O'D (∵Radii of congruent circles)
AB = CD (Given)
△OAB ≅ △O'CD (By SSS congruence criterion)
⇒ ∠AOB = ∠OO'D (cpct)
So, the circle can have 0, 1 or 2 points in common.
The maximum number of common points is 2.

To draw the centre of a given circle:
- Draw the circle.
- Take any two different chords AB and CD of this circle and draw perpendicular bisectors of these chords.
- Let these perpendicular bisectors meet at point O.'
(i) AP = CP
(ii) BP = DP
Answer
In △OMP and △ONP,
OP = OP (common side)
∠OMP = ∠ONP (both are right angles)
OM = ON (side both the chords are equal, so the distance of the chords from the centre are also equal)
△OMP ≅ △ONP (RHS congruence criterion)
⇒ MP = PN (cpct) ...(a)
(i) Since AB = CD (given)
⇒ AM = CN (⊥ drawn from the centre to the chord bisects the chord)
⇒ AM + MP = CN + NP (from (a))
⇒ AP = CP ....(b)
(ii) Since AB = CD
⇒ AP + BP = CP + DP
⇒ BP = DP (from (b))
Hence, proved.
(i) the same side of the centre.
(ii) the opposite sides of the centre.
Answer
Given that AB = 16cm and CD = 12cm
So, AL = 8cm and CM = 6cm (⊥ from the centre to the chord bisects the chord)
In right triangles OLA and OMC,
By Pythagoras theorem,
OA2 = OL2 + AL2 and OC2 = OM2 + CM2
⇒ 102 = OL2 + 82 and 102 = OM2 + 62
⇒ OL2 = 100 - 64 and OM2 = 100 - 36
⇒ OL2 = 36 and OM2 = 64
⇒ OL = 6cm and OM = 8cm
(i) In the first case, distacne between AB and CD is
LM = OM - OL = 8-6 = 2cm
(ii) In the second case, distance between AB and CD is
LM = OM + CL = 8+6 = 14cm
If AB = 32 cm, find the length of CD
Answer
To find: CD
Given AB = 32 cm
⇒ AC = 16cm (Since ⊥drawn from the centre to the chord, bisects the chord)
In right △OCA,
OA2 = OC2 + AC2 (By Pythagoras theorem)
⇒ OC2 = OA2 - AC2
⇒ OC2 = 202 - 162
⇒ OC2 =144
⇒ OC = 12 cm
Since, OD = 20cm and OC = 12 cm
⇒ CD = OD - OC = 20 - 12 = 8cm
8. In the given figure, AB and CD are two equal chords of a circle, with centre O.
If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.
AnswerIt is given in the question that point.
P is the mid-point of the chord AB and Point Q is the mid-point of the CD.
⇒ ∠APO = 90° (as the straight line drawn from the center of a circle to bisect a chord, which is not a diameter, is at the right angle to the chord.)
As chords, AB and CD are equal therefore they are equidistant from the center i.e; PO = OQ (∵ Equal chords of a circle are equidistant from the center)
Now, the ΔPOQ is an isosceles triangle with OP = OQ as its two equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
⇒ ∠POQ + ∠OPQ + ∠PQO = 180°
⇒ ∠OPQ + ∠POQ + 150° = 180° (Given: ∠POQ = 150°)
⇒ 2∠OPQ = 180° – 150° (As, ∠OPQ = ∠PQO)
⇒ 2∠OPQ = 30°
⇒ ∠OPQ = 15°
As ∠APO = 90°
⇒ ∠APQ + ∠OPQ = 90°
⇒ ∠APQ = 90° – 15° (As, ∠OPQ = 15°)
⇒ ∠APQ = 75°.
Given:
1. AOC is the diameter.
2. Arc AXB = 1/2 Arc BYC
From Arc AXB = 1/2 Arc BYC We can see that
Arc AXB : Arc BYC = 1:2
⇒ ∠BOA : ∠BOC = 1:2
Since, AOC is the diameter of the circle hence,
∠AOC = 180°
Now,
Assume that ∠BOA = x° and ∠BOC = 2x°
∠AOC = ∠BOA + ∠BOC = 180°
⇒ x + 2x = 180°
⇒ 3x = 180°
⇒ x = 60°
Hence, ∠BOA = 60° and ∠BOC = 120°.
(arc APB)/2 = (arc BQC)/3 = (arc CRA)/4
Find ∠BOC.
we can draw the circle with arc APB, arc BQC and arc CRA
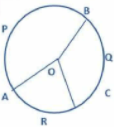
The given equation is
(Arc APB)/2 = (Arc BQC)/3 = (Arc ORA)/4
let (Arc APB)/2 = (Arc BQC)/3 = (Arc ORA)/4 = k (say)
Then,
Arc APB = 2k, Arc BQC = 3k, Arc CRA = 4k
or Arc APB : Arc BQC : Arc CRA = 2 : 3 : 4
⇒ ∠AOB : ∠BOC : ∠AOC = 2 : 3 : 4
and therefore,
∠AOB = 2k°, ∠BOC = 3k°, and ∠AOC = 4k°
Now,
Angle in a circle is 360°
So, 2k + 3k + 4k = 360°
⇒ 9k = 360°
⇒ k = 40°
Hence,
∠BOC = 3 x 40° = 120°.