ICSE Solutions for Chapter 16 Loci (Locus and its Construction) Class 10 Mathematics
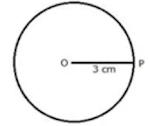
Question 1: Describe the locus of a point at a distance of 3 cm from a fixed point.
Solution 1:
Question 2: Describe the locus of a point at a distance of 2 cm from a fixed line.
Solution 2:

Question 3: Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.

ii) Y is equidistant from A and C
Solution 3:

Proof:
(i) In ΔAXL and ΔAXM.
∠XAL = ∠XAM ...(Given)
AX = AX ...(Common)
∠XLA = ∠XMA ...(Each = 90°)
∴ By Angle-Side-Angle criterion of congruence,
ΔAXL ≅ ΔAXM ...(ASA Postulate)
ΔAXL ≅ ΔAXM ...(ASA Postulate)
The corresponding parts of the congruent triangles are congruent.
∴ XL = XM ...(CPCT)
∴ XL = XM ...(CPCT)
Hence, X is equidistant from AB and AC.
(ii) In ΔYTA and ΔYTC
AT = CT ...(∵ PQ is a perpendicular bisector of AC)
∠YTA = ∠YTC ...(Each = 90°)
(ii) In ΔYTA and ΔYTC
AT = CT ...(∵ PQ is a perpendicular bisector of AC)
∠YTA = ∠YTC ...(Each = 90°)
YT = YT ...(Common)
∴ By Side-Angle-Side criterion of congruence,
∴ ΔYTA ≅ ΔYTC ...(SAS Postulate)
∴ ΔYTA ≅ ΔYTC ...(SAS Postulate)
The corresponding parts of the congruent triangles are congruent.
∴ YA = YC ...(CPCT)
∴ YA = YC ...(CPCT)
Hence, Y is equidistant from A and C.
Question 4: Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that is equidistant from B and C.
Solution 4: Given: In triangle ABC, AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm
 Steps of Construction:
Steps of Construction:
(i) Draw a line segment BC = 6.3 cm
(ii) With centre B and radius 4.2 cm, draw an arc.
(iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
(iv) Join AB and AC. ΔABC is the required triangle.
(v) Again with centre B and C and radius greater than ½ BC, draw arcs which intersect each other at L and M.
(vi) Join LM intersecting AC at D and BC at E.
(vii) Join DB.
Question 4: Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that is equidistant from B and C.
Solution 4: Given: In triangle ABC, AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm

(i) Draw a line segment BC = 6.3 cm
(ii) With centre B and radius 4.2 cm, draw an arc.
(iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
(iv) Join AB and AC. ΔABC is the required triangle.
(v) Again with centre B and C and radius greater than ½ BC, draw arcs which intersect each other at L and M.
(vi) Join LM intersecting AC at D and BC at E.
(vii) Join DB.
Proof: In ΔDBE and ΔDCE
BE = EC ...(LM is bisector of BC)
BE = EC ...(LM is bisector of BC)
∠DEB = ∠DEC ...(Each = 90˚)
DE = DE ...(Common)
∴ By Side – Angle – Side criterion of congruence, we have
ΔDBE ≅ ΔDCE ...(SAS Postulate)
The corresponding parts of the congruent triangles are congruent.
∴ DB = DC ...(CPCT)
ΔDBE ≅ ΔDCE ...(SAS Postulate)
The corresponding parts of the congruent triangles are congruent.
∴ DB = DC ...(CPCT)
Hence, D is equidistant from B and C.
Question 5: Describe the locus of a stone dropped from the top of a tower.
Solution 5:
 The locus of a stone which is dropped from the top of a tower will be a vertical line through the point from which the stone is dropped.
The locus of a stone which is dropped from the top of a tower will be a vertical line through the point from which the stone is dropped.
Question 6: Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Solution 6:

Question 7: Describe the locus of the door handle as the door opens.
Solution 7:
 The locus of the door handle will be the circumference of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.
The locus of the door handle will be the circumference of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.
Question 8: Describe the locus of a point inside a circle and equidistant from two fixed points on the circumference of the circle.
Solution 8:
 The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be diameter which is perpendicular bisector of the line joining the two fixed points on the circle.
The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be diameter which is perpendicular bisector of the line joining the two fixed points on the circle.
Question 9: In triangle LMN, bisectors of interior angles at L and N intersect each other at point A.
Prove that:
(i) point A is equidistant from all the three sides of the triangle
(ii) AM bisects angle LMN.
Solution 9:
 Construction: Join AM
Construction: Join AM
Proof:
∵ A lies on bisector of ∠N
∴ A is equidistant from MN and LN
Again, A lies on bisector of ∠L
∴ A is equidistant from LN and LM.
Hence, A is equidistant from all sides of the triangle LMN.
∴ A lies on the bisector of ∠M
Question 10:
Use ruler and compasses only for this question.
(i) Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Solution 10:
Steps of construction:
(i) Draw line BC = 6 cm and an angle CBX = 60°. Cut off AB = 3.5. Join AC, triangle ABC is the required triangle.
(ii) Draw perpendicular bisector of BC and bisector of angle B.
(iii) Bisector of angle B meets bisector of BC at P.
BP is the required length, where, PB = 3.5 cm
(iv) P is the point which is equidistant from BA and BC, also equidistant from B and C.

Question 5: Describe the locus of a stone dropped from the top of a tower.
Solution 5:

Question 6: Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Solution 6:

The locus of the runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge will be the circumference of a circle whose radius is equal to the radius of the inner circular track plus 1.5 m.
Question 7: Describe the locus of the door handle as the door opens.
Solution 7:

Question 8: Describe the locus of a point inside a circle and equidistant from two fixed points on the circumference of the circle.
Solution 8:

Question 9: In triangle LMN, bisectors of interior angles at L and N intersect each other at point A.
Prove that:
(i) point A is equidistant from all the three sides of the triangle
(ii) AM bisects angle LMN.
Solution 9:

Proof:
∵ A lies on bisector of ∠N
∴ A is equidistant from MN and LN
Again, A lies on bisector of ∠L
∴ A is equidistant from LN and LM.
Hence, A is equidistant from all sides of the triangle LMN.
∴ A lies on the bisector of ∠M
Question 10:
Use ruler and compasses only for this question.
(i) Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Solution 10:
Steps of construction:
(i) Draw line BC = 6 cm and an angle CBX = 60°. Cut off AB = 3.5. Join AC, triangle ABC is the required triangle.
(ii) Draw perpendicular bisector of BC and bisector of angle B.
(iii) Bisector of angle B meets bisector of BC at P.
BP is the required length, where, PB = 3.5 cm
(iv) P is the point which is equidistant from BA and BC, also equidistant from B and C.


