ICSE Solutions for Chapter 15 Similarity Class 10 Mathematics
In the figure, given below, straight lines AB and CD intersect at P; and AC∥BD. Prove that:
(i) ∆APC and ∆BPD are similar.
(ii) If BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
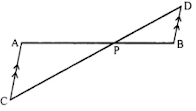
Solution 1:
(i) In ΔAPC and ΔBPD,
∠APC = ∠BPD ...(vertically opposite angles)
∠ACP = ∠BDP …(alternate angles since AC∥BD)
∴ ΔAPC ~ ΔBPD ...(AA criterion for similarity)
(ii) In ΔAPC and ΔBPD,
∠ACP = ∠BPD ...(vertically opposite angles)
∠ACP = ∠BDP …(alternate angles since AC∥BD)
∴ ΔAPC ~ ΔBPD ...(AA criterion for similarity)
So, PA/PB = PC/PD = AC/AD
⇒ PA/3.2 = PC/4 = 3.6/2.4
So, PA/3.2 = 3.6/2.4 and PC/4 = 3.6/2.4
⇒ PA = (3.6×3.2)/2.4 = 4.8 cm
And, PC = (3.6×4)/2.4 = 6 cm
Hence, PA = 4.8 cm and PC = 6 cm
Question 2:
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:
(i) ∆APB is similar to ∆CPD
(ii) PA×PD = PB×PC
Solution 2:
(i)

∠APB = ∠CPD ...(vertically opposite angles)
∠ABP = ∠CDP …(alternate angles since AB∥DC)
∴ ΔAPB ~ ΔCPD ...(AA criterion for similarity)
(ii)

∠APB = ∠CPD ...(vertically opposite angles)
∠ABP = ∠CDP ...(alternate angles since AB∥DC)
∴ ΔAPB ~ ΔCPD …(AA criterion for similarity)
⇒ PA/PC = PB/PD ….(Since corresponding sides of similar triangles are equal.)
⇒ PA×PD = PB×PC
Question 3:
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:
(i) DP: PL = DC: BL.
(ii) DL: DP = AL : DC.
Solution 3:
(i)
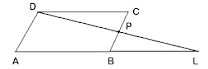
By the basic Proportionality theorem, we get
DL/DP = AL/AB
Since, ABCD is a parallelogram, AB = DC.
So, DL/DP = AL/DC.
(ii)

Since, AD∥BC, that is, AD∥ BP,
by the Basic Proportionality theorem, we get
DP/PL = AB/BL
Since, ABCD is a parallelogram, AB = DC.
So, DP/PL = DC/BL.
Question 4:
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that:
(i) ∆AOB is similar to ∆COD.
(ii) OA×OD – OB×OC.
Solution 4:
(i)

AO/CO = 2/1 = BO/DO
Also, ∠AOB = ∠DOC ...(vertically opposite angles)
So, ΔAOB ~ ΔCOD ...(SAS criterion for similarity)
(ii)

AO/CO = 2/1 = BO/CO
So, OA×OD = OB×OC.
Question 5:
In ∆ABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that:
(i) CB : BA= CP : PA
(ii) AB × BC = BP × CA
Solution 5:
(i)

∠ABC = 2∠ACB
Let ∠ACB = x
⇒ ∠ABC = 2∠ACB = 2x
Given BP is bisector of ∠ABC.
Hence, ∠ABP = ∠PBC = x
Using the angle bisector theorem, that is, the bisector of an angle divides the side opposite to it in the ratio of other two sides.
Hence, CB : BA = CP : PA.
(ii)

∠ABC = 2∠ACB
Let ∠ACB = x
⇒ ∠ABC = 2∠ACB = 2x
Given BP is bisector of ∠ABC.
Hence ∠ABP = ∠PBC = x
Using the angle bisector theorem, that is the bisector of an angle divides the side opposite to it in the ratio of other two sides.
Hence, CB : BA = CP : PA.
Consider ΔABC and ΔAPB,
∠ABC = ∠APB …[Exterior angle property]
∠BCP = ∠ABP …[Given]
∴ ΔABC ~ ΔAPB [AA criterion for similarity]
CA/AB = BC/BP ...(Corresponding sides of similar triangles are proportional.)
⇒ AB × BC = BP × CA
Question 6:
In ∆ABC; BM ⊥ AC and CN ⊥ AB; show that:
AB/AC = BM/CN = AM/AN
Solution 6:

∠AMB = ∠ANC ...(BM⊥AC and CN⊥AB)
∠BAM = ∠CAN …(Common angle)
⇒ ∆ABM ~ ∆ACN ...(AA criterion fro similarity)
⇒ AB/AC = BM/CN = AM/AN
Question 7:
In the given figure, DE//BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find lengths of ME and DM.

Solution 7:
(i) In ∆AME and ∆ANC,
∠AME = ∠ANC ….(Since DE∥BC that is, ME∥NC.)
∠MAE = ∠NAC …..(common angle)
⇒ ∆AME ~ ∆ANC ...(AA criterion for similarity)
In ∆ADM and ∆ABN,
∠ADM = ∠ABN ...(Since DE∥BC that is, DM∥BN.)
∠DAM = ∠BAN …(common angle)
⇒ ∆ADM ~ ∆ABN ...(AA criterion for similarity)
In ∆ADE and ∆ABC,
∠ADE = ∠ABC …(Since DE∥BC that is, ME ∥NC.)
∠AED = ∠ACB …(Since DE∥BC .)
⇒ ∆ADE ~ ∆ABC …(AA criterion fro similarity)
(ii) In ∆AME and ∆ANC,
∠AME = ∠ANC ….( Since DE∥BC that is ME∥NC.)
∠MAE = ∠NAC …(common angle)
⇒ ∆AME ~ ∆ANC ...(AA criterion for similarity)
⇒ ME/NC = AE/AC
⇒ ME/6 = 15/24
⇒ ME = 3.75 cm
In ∆ADE and ∆ABN,
∠ADE = ∠ABC ...(Since DE∥BC that is ME∥NC)
∠AED = ∠ACB ...(Since DE∥BC)
⇒ ∆ADE ~ ∆ABC ...(AA criterion for similarity)
⇒ AD/AB = AE/AC = 15/24 ...(i)
In ∆ADM and ∆ABN,
∠ADM = ∠ABN ...(Since DE∥BC that is ME∥NC.)
∠DAM = ∠BAN ...(common angle)
⇒ ∆ADM ~ ∆ABN ...(AA criterion for similarity)
⇒ DM/BN = AD/AB = 15/24 ...(from (i))
⇒ DM/24 = 15/24
⇒ DM = 15 cm
Question 8:
In the given figure, AD = AE and AD2 = BD × EC
Prove that: triangles ABD and CAE are similar.

Solution 8:
In ∆ABD and ∆CAE,
∠ADE = ∠AED …(Angles opposite equal sides are equal.)
So, ∠ADB = ∠AEC ...(Since ∠ADB + ∠ADE = 180˚ and ∠AEC + ∠AED = 180˚)
Also, AD2 = BD × EC
⇒ AD/BD = EC/AD
⇒ AD/BD = EC/AE
⇒ ∆ABD ~ ∆CAE ...(SAS criterion for similarity)
Question 9:
In the given figure, AB∥DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

Solution 9:
In ∆DOQ and ∆BOP,∠QDO = ∠PBO …(Since AB∥DC that is, PB∥DQ.)
So, ∠DOQ = ∠BOP ...(vertically opposite angles)
⇒ ∆DOQ ~ ∆BOP …(AA criterion for similarity)
⇒ DO/ BO = DQ/BP
⇒ DO/6 = 8/BP
⇒ BP×DO = 48 cm2
Question 10:
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR=9 cm; find the length of PB
Solution 10:

AC = AB ...(Given)
⇒ ∠ABC = ∠ACB ...(Angles opposite equal sides are equal.)
In ∆PRC and ∆PQB,
∠ABC = ∠ACB
∠PRC = ∠PQB ...(Both are right angles.)
⇒ ∆PRC ~ ∆PQB …(AA criterion for similarity)
⇒ PR/PQ = RC/QB = PC/PB
⇒ PR/PQ = PC/PB
⇒ 9/15 = 12/PB
⇒ PB = 20 cm
Question 11:
State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
Solution 11:
(i) False
(ii) True
(iii) True
(iv) False
(v) True
(vi) True
(vii) True
Question 12: Given = ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x + 1 and DE = 4x + 2.
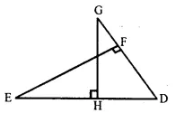
Solution 12:
In ∆DHG and ∆DFE,
∠GHD = ∠DFE = 90˚
∠D = ∠D (Common)
∴ ∆DHG ~ ∆DFE
⇒ DH/DF = DG/DE
⇒ 8/12 = (3x – 1)/(4x + 2)
⇒ 32x + 16 = 36x – 12
⇒ 28 = 4x
⇒ x = 7
∴ DG = 3×7 – 1 = 20
DE = 4×7 + 2 = 30

