NCERT Notes for Class 9 Maths Chapter 3 Introduction to Euclid's Geometry

Class 9 Maths Chapter 3 Introduction to Euclid's Geometry Notes
Chapter Name | Introduction to Euclid's Geometry Notes |
Class | CBSE Class 9 |
Textbook Name | NCERT Mathematics Class 9 |
Related Readings |
|
Introduction to Euclid’s Geometry

Euclid was a teacher of mathematics at Alexandria in Egypt, popularly known as ‘Father of Geometry”.
He introduced the method of proving mathematical results by using deductive logical reasoning and the previously proved result.
He collected all his work in a book called “Elements”. This book is divided into thirteen chapters and each chapter is called a book.
Definitions of Euclid’s
Euclid thought that the geometry is an abstract model of the world which we can see around us. Like the notions of line, plane, surface etc.
He had given these notions in the form of definitions-
- Anything which has no component is called Point.
- A length without breadth is called Line.
- The endpoints of any line are called Points which make it line segment.
- If a line lies evenly with the points on itself then it is called A Straight Line.
- Any object which has length and breadth only is called Surface.
- The edges of a surface are lines.
- A plane surface is a surface which lies evenly with the straight lines on itself.
Euclid’s Axioms and Postulates
Euclid assumed some properties which were actually ‘obvious universal truth’. He had bifurcated them in two types: Axioms and postulates.
Axioms
Some common notions which are used in mathematics but not directly related to mathematics are called Axioms.
Some of the Axioms are:
1. If the two things are equal to a common thing then these are equal to one another.
If p = q and s = q, then p = s.
2. If equals are added to equals, the wholes are equal.
If p = q and we add s to both p and q then the result will also be equal.
p + s = q + s
3. If equals are subtracted from equals, the remainders are equal.
This is same as above, if p = q and we subtract the same number from both then the result will be the same.
p – s = q - s
4. Things which coincide with one another are equal to one another.
If two figures fit into each other completely then these must be equal to one another.
5. The whole is greater than the part.

This circle is divided into four parts and each part is smaller than the whole circle. This shows that the whole circle will always be greater than any of its parts.
6. Things which are double of the same things are equal to one another.
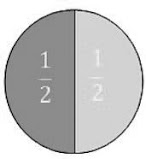
This shows that this is the double of the two semicircles, so the two semicircles are equal to each other.
7. Things which are halves of the same things are equal to one another. This is the vice versa of the above axiom.
Postulates
The assumptions which are very specific in geometry are called Postulates.
There are five postulates by Euclid-
1. A straight line may be drawn from any one point to any other point.

This shows that a line can be drawn from point A to point B, but it doesn’t mean that there could not be other lines from these points.
2. A terminated line can be produced indefinitely.

This shows that a line segment which has two endpoints can be extended indefinitely to form a line.
3. A circle can be drawn with any centre and any radius.

This shows that we can draw a circle with any line segment by taking one of its points as a centre and the length of the line segment as the radius. As we have AB line segment, in which we took A as the centre and the AB as the radius of the circle to form a circle.
4. All right angles are equal to one another.

As we know that a right angle is equal to 90° and all the right angles are congruent because if any angle is not 90° then it is not a right angle.
As in the above figure ∠DCA =∠DCB =∠HE =∠HGF= 90°
5. Parallel Postulate
If there is a line segment which passes through two straight lines while forming two interior angles on the same side whose sum is less than 180°, then these two lines will definitely meet with each other if extended on the side where the sum of two interior angles is less than two right angles.
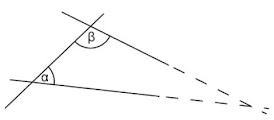
And if the sum of the two interior angles on the same side is 180° then the two lines will be parallel to each other.
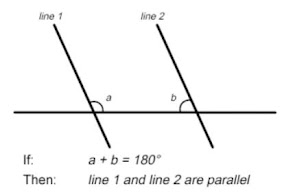
Equivalent Versions of Euclid’s Fifth Postulate
1. Play fair’s Axiom
This says that if you have a line ‘l’ and a point P which doesn’t lie on line ‘l’ then there could be only one line passing through point P which will be parallel to line ‘l’. No other line could be parallel to line ‘l’ and passes through point P.

2. Two distinct intersecting lines cannot be parallel to the same line.
This also states that if two lines are intersecting with each other than a line parallel to one of them could not be parallel to the other intersecting line.
