NCERT Solutions for Chapter 14 Practical Geometry Class 6 Maths

Practical Geometry Questions and Answers
Chapter Name | Practical Geometry NCERT Solutions |
Class | CBSE Class 6 |
Textbook Name | Maths |
Related Readings |
|
Exercise 14.1
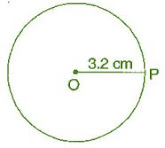
Question 1: Draw a circle of radius 3.2 cm.
Solution
Steps of construction:
(a) Open the compass for the required radius of 3.2 cm.
(b) Make a point with a sharp pencil where we want the centre of circle to be.
(c) Name it O.
(d) Place the pointer of compasses on O.
(e) Turn the compasses slowly to draw the circle.
Hence, it is the required circle.
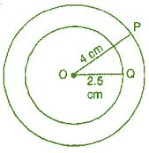
Question 2: With the same centre O, draw two circles of radii 4 cm and 2.5 cm.
Solution
Steps of construction:
(a) Marks a point ‘O’ with a sharp pencil where we want the centre of the circle.
(b) Open the compasses 4 cm.
(c) Place the pointer of the compasses on O.
(d) Turn the compasses slowly to draw the circle.
(e) Again open the compasses 2.5 cm and place the pointer of the compasses on D.
(f) Turn the compasses slowly to draw the second circle.
Hence, it is the required figure.
Question 3: Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained if the diameters are perpendicular to each other? How do you check your answer?
Solution
(i) By joining the ends of two diameters, we get a rectangle. By measuring, we find AB = CD = 3 cm, BC = AD = 2 cm, i.e., pairs of opposite sides are equal and also ∠A = ∠B = ∠C = ∠D = 90°, , i.e. each angle is of 90° .
Hence, it is a rectangle.

(ii) If the diameters are perpendicular to each other, then by joining the ends of two diameters, we get a square.
By measuring, we find that AB = BC = CD = DA = 2.5 cm, i.e., all four sides are equal.
Also ∠A = ∠B = ∠C = ∠D = 90°, , i.e. each angle is of 90°.
Hence, it is a square.

Question 4: Draw any circle and mark points A, B and C such that:
(a) A is on the circle.
(b) B is in the interior of the circle.
(c) C is in the exterior of the circle.
Solution
(i) Mark a point ‘O’ with sharp pencil where we want centre of the circle.
(ii) Place the pointer of the compasses at ‘O’. Then move the compasses slowly to draw a circle.
(a) Point A is on the circle.
(b) Point B is in interior of the circle.
(c) Point C is in the exterior of the circle.

Question 5: Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether AB and CD are at right angles.
Solution
Draw two circles of equal radii taking A and B as their centre such that one of them passes through the centre of the other. They intersect at C and D. Join AB and CD.
Yes, AB and CD intersect at right angle as ∠COB is 90°.

Question 1: Draw a line segment of length 7.3 cm, using a ruler.
Solution
Steps of construction:
(i) Place the zero mark of the ruler at a point A.
(ii) Mark a point B at a distance of 7.3 cm from A.
(iii) Join AB.
Hence, AB is the required line segment of length 7.3 cm.
Question 2: Construct a line segment of length 5.6 cm using ruler and compasses.
Solution
Steps of construction:
(i) Draw a line l. Mark a point A on this line.
(ii) Place the compasses pointer on zero mark of the ruler. Open it to place the pencil point up to 5.6 cm mark.
(iii) Without changing the opening of the compasses. Place the pointer on A and cut an arc l at B.
AB is the required line segment of length 5.6 cm.
Question 3: Construct AB of length 7.8 cm. From this cut off AC of length 4.7 cm. Measure BC.
Solution
Steps of construction:

(i) Place the zero mark of the ruler at A.
(ii) Mark a point B at a distance 7.8 cm from A.
(iii) Again, mark a point C at a distance 4.7 from A.
Hence, by measuring BC , we find that BC = 3.1 cm
Question 4: Given AB of length 3.9 cm, construct PQ such that the length PQ is twice that of AB . Verify by measurement.
(Hint: Construct PX such that length of PX = length of AB ; then cut off XQ such that XQ also has the length of AB .
Solution
Steps of construction:

(i) Draw a line l.
(ii) Construct PX such that length of PX = length of AB.
(iii) Then cut of XQ such that XQ also has the length of AB.
(iv) Thus the length of PX and the length of XQ added together make twice the length of AB.
Verification:
Hence, by measurement we find that PQ = 7.8 cm
= 3.9 cm + 3.9 cm ×
AB + AB = 2 × AB
Question 5: Given AB of length 7.3 cm and CD of length 3.4 cm, construct a line segment XY such that the length of XY is equal to the difference between the lengths of AB and CD.
Verify by measurement.
Solution
Steps of construction:
(i) Draw a line l and take a point X on it.
(ii) Construct XZ such that length XZ = length of AB = 7.3 cm
(iii) Then cut off ZY = length of CD = 3.4 cm
(iv) Thus the length of XY = length of AB – length of CD

Verification:
Hence, by measurement we find that length of XY
= 3.9 cm
= 73. Cm – 3.4 cm
AB – CD
Exercise 14.3
Question 1: Draw any line segment PQ. Without measuring PQ, construct a copy of PQ.
Solution
Steps of construction:

(i) Given PQ whose length is not known.
(ii) Fix the compasses pointer on P and the pencil end on Q. The opening of the instrument now gives the length of PQ.
(iii) Draw any line l Choose a point A on l Without changing the compasses setting, place the pointer on A.
(iv) Draw an arc that cuts l at a point, say B.
Hence, AB is the copy of PQ .
Question 2: Given some line segment AB, whose length you do not know, construct PQ such that the length of PQ is twice that of AB.
Solution
Steps of construction:

(i) Given AB whose length is not known.
(ii) Fix the compasses pointer on A and the pencil end on B. The opening of the instrument now gives the length of AB.
(iii) Draw any line l Choose a point P on l Without changing the compasses setting, place the pointer on Q.
(iv) Draw an arc that cuts l at a point R.
(v) Now place the pointer on R and without changing the compasses setting, draw another arc that cuts l at a point Q.
Hence, PQ is the required line segment whose length is twice that of AB.
Exercise 14.4
Question 1: Draw any line segment AB. Mark any point M on it. Through M, draw a perpendicular to AB. (Use ruler and compasses)
Solution
Steps of construction:
(i) With M as centre and a convenient radius, draw an arc intersecting the line AB at two points C and B.
(ii) With C and D as centres and a radius greater than MC, draw two arcs, which cut each other at P.
(iii) Join PM. Then PM is perpendicular to AB through the point M.

Question 2: Draw any line segment PQ. Take any point R not on it. Through R, draw a perpendicular to PQ. (Use ruler and set-square)
Solution
Steps of construction:
(i) Place a set-square on PQ such that one arm of its right angle aligns along PQ .
(ii) Place a ruler along the edge opposite to the right angle of the set-square.
(iii) Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set square.
(iv) Join RM along the edge through R meeting PQ at M. Then RM ⟂ PQ.

Question 3: Draw a line l and a point X on it. Through X, draw a line segment XY perpendicular to l. Now draw a perpendicular to XY to Y. (use ruler and compasses)
Solution
Steps of construction:
(i) Draw a line l and take point X on it.
(ii) With X as centre and a convenient radius, draw an arc intersecting the line l at two points A and B.
(iii) With A and B as centres and a radius greater than XA, draw two arcs, which cut each other at C.
(iv) Join AC and produce it to Y. Then XY is perpendicular to l .
(v) With D as centre and a convenient radius, draw an arc intersecting XY at two points C and D.
(vi) With C and D as centres and radius greater than YD, draw two arcs which cut each other at F.
(vii) Join YF, then YF is perpendicular to XY at Y.

Question 1: Draw AB of length 7.3 cm and find its axis of symmetry.
Solution
Axis of symmetry of line segment AB will be the perpendicular bisector of AB. So, draw the perpendicular bisector of AB.
Steps of construction:
(i) Draw a line segment AB = 7.3 cm
(ii) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.
(iii) Join CD. Then CD is the axis of symmetry of the line segment AB.

Question 2: Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solution
Steps of construction:
(i) Draw a line segment AB = 9.5 cm
(ii) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.
(iii) Join CD. Then CD is the perpendicular bisector of AB .

Question 3: Draw the perpendicular bisector of XY whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b)If M is the mid-point of XY , what can you say about the lengths MX and XY?
Solution
Steps of construction:

(i) Draw a line segment XY = 10.3 cm
(ii) Taking X and Y as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.
(iii) Join CD. Then CD is the required perpendicular bisector of XY .
Now:
(a) Take any point P on the bisector drawn. With the help of divider we can check that PX = PY .
(b)If M is the mid-point of XY, then MX = 1/2 XY.
Question 4: Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Solution
Steps of construction:

(i) Draw a line segment AB = 12.8 cm
(ii) Draw the perpendicular bisector of AB which cuts it at C. Thus, C is the mid- point of AB.
(iii) Draw the perpendicular bisector of AC which cuts it at D. Thus D is the mid- point of .
(iv) Again, draw the perpendicular bisector of CB which cuts it at E. Thus, E is the mid-point of CB.
(v) Now, point C, D and E divide the line segment AB in the four equal parts.
(vi) By actual measurement, we find that
AD = DC = CE = EB = 3.2 cm
Question 5: With PQ of length 6.1 cm as diameter, draw a circle.
Solution
Steps of construction:
(i) Draw a line segment PQ = 6.1 cm.
(ii) Draw the perpendicular bisector of PQ which cuts, it at O. Thus O is the mid-point of PQ.
(iii) Taking O as centre and OP or OQ as radius draw a circle where diameter is the line segment PQ.

Question 6: Draw a circle with centre C and radius 3.4 cm. Draw any chord AB. Construct the perpendicular bisector AB and examine if it passes through C.
Solution
Steps of construction:
(i) Draw a circle with centre C and radius 3.4 cm.
(ii) Draw any chord AB.
(iii) Taking A and B as centres and radius more than half of AB, draw two arcs which cut each other at P and Q.
(iv) Join PQ. Then PQ is the perpendicular bisector of AB.
(v) This perpendicular bisector of AB passes through the centre C of the circle.

Question 7: Repeat Question 6, if AB happens to be a diameter.
Solution
Steps of construction:
(i) Draw a circle with centre C and radius 3.4 cm.
(ii) Draw its diameter AB.
(iii) Taking A and B as centres and radius more than half of it, draw two arcs which intersect each other at P and Q.
(iv) Join PQ. Then PQ is the perpendicular bisector of AB.
(v) We observe that this perpendicular bisector of AB passes through the centre C of the circle.

Question 8: Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution
Steps of construction:
(i) Draw the circle with O and radius 4 cm.
(ii) Draw any two chords AB and CD in this circle.
(iii) Taking A and B as centres and radius more than half AB, draw two arcs which intersect each other at E and F.
(iv) Join EF. Thus EF is the perpendicular bisector of chord CD.
(v) Similarly draw GH the perpendicular bisector of chord CD.
(vi) These two perpendicular bisectors meet at O, the centre of the circle.

Question 9: Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of OA and OB. Let them meet at P. Is PA = PB?
Solution
Steps of construction:
(i) Draw any angle with vertex O.
(ii) Take a point A on one of its arms and B on another such that OA = OB.
(iii) Draw perpendicular bisector of OA and OB.
(iv) Let them meet at P. Join PA and PB.
(v) With the help of divider, we check that PA = PB.

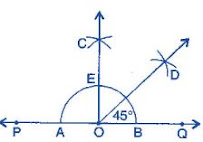
Question 1: Draw ∠POQ of measure 75° and find its line of symmetry.
Solution
Steps of construction:
(a) Draw a line l and mark a point O on it.
(b) Place the pointer of the compasses at O and draw an arc of any radius which intersects the line l at A.
(c) Taking same radius, with centre A, cut the previous arc at B.
(d) Join OB, then ∠BOA = 60° .
(e) Taking same radius, with centre B, cut the previous arc at C.
(f) Draw bisector of ∠BOC. The angle is of 90° . Mark it at D. Thus, ∠DOA = 90°
(g) Draw OP as bisector of ∠DOB. Thus, ∠POA = 75°.

Question 2: Draw an angle of measure 147° and construct its bisector.
Solution
Steps of construction:
(a) Draw a ray OA.
(b) With the help of protractor, construct ∠AOB = 147° .
(c) Taking centre O and any convenient radius, draw an arc which intersects the arms OA and OB at P and Q respectively.
(d) Taking P as centre and radius more than half of PQ, draw an arc.
(e) Taking Q as centre and with the same radius, draw another arc which intersects the previous at R.
(f) Join OR and produce it.
(g) Thus, OR is the required bisector of ∠AOB.

Question 3: Draw a right angle and construct its bisector.
Solution
Steps of construction:
(a) Draw a line PQ and take a point O on it.
(b) Taking O as centre and convenient radius, draw an arc which intersects PQ at A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(d) Join OC. Thus, ∠COQ is the required right angle.
(e) Taking B and E as centre and radius more than half of BE, draw two arcs which intersect each other at the point D.
(f) Join OD. Thus, OD is the required bisector of ∠COQ.
Question 4: Draw an angle of measure 153° and divide it into four equal parts.
Solution
Steps of construction:
(a) Draw a ray OA.
(b) At O, with the help of a protractor, construct ∠AOB = 153° .
(c) Draw OC as the bisector of ∠AOB.
(d) Again, draw OD as bisector of ∠AOC.
(e) Again, draw OE as bisector of ∠BOC.
(f) Thus, OC , OD and OE divide ∠AOB in four equal parts.

Question 5: Construct with ruler and compasses, angles of following measures:
(a) 60°
(b) 30°
(c) 90°
(d) 120°
(e) 45°
(f) 135°
Solution
Steps of construction:
(a) 60°
(i) Draw a ray OA.
(ii) Taking O as centre and convenient radius, mark an arc, which intersects OA at P.
(iii) Taking P as centre and same radius, cut previous arc at Q.
(iv) Join OQ. Thus, ∠BOA is required angle of 60° .

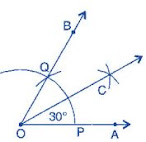
(b) 30°
(i) Draw a ray OA.
(ii) Taking O as centre and convenient radius, mark an arc, which intersects OA at P.
(iii) Taking P as centre and same radius, cut previous arc at Q.
(iv) Join OQ. Thus, ∠BOA is required angle of 60° .
(v) Put the pointer on P and mark an arc.
(vi) Put the pointer on Q and with same radius, cut the previous arc at C. Thus, ∠COA is required angle of 30° .
(c) 90°
(i) Draw a ray OA.
(ii) Taking O as centre and convenient radius, mark an arc, which intersects OA at X.
(iii) Taking X as centre and same radius, cut previous arc at Y.
(iv) Taking Y as centre and same radius, draw another arc intersecting the same arc at Z.
(v) Taking Y and Z as centres and same radius, draw two arcs intersecting each other at S.
(vi) Join OS and produce it to form a ray OB. Thus, ∠BOA is required angle of 90° .

(d) 120°
(i) Draw a ray OA.
(ii) Taking O as centre and convenient radius, mark an arc, which intersects OA at P.
(iii) Taking P as centre and same radius, cut previous arc at Q.
(iv) Taking Q as centre and same radius cut the arc at S.
(v) Join OS. Thus, ∠AOD is required angle of 120° .

(e) 45°
(i) Draw a ray OA.
(ii) Taking O as centre and convenient radius, mark an arc, which intersects OA at X.
(iii) Taking X as centre and same radius, cut previous arc at Y.
(iv) Taking Y as centre and same radius, draw another arc intersecting the same arc at Z.
(v) Taking Y and Z as centres and same radius, draw two arcs intersecting each other at S.
(vi) Join OS and produce it to form a ray OB. Thus, ∠BOA is required angle of 90° .
(vii) Draw the bisector of ∠BOA. Thus, ∠MOA is required angle of 45° .

(f) 135°
(i) Draw a line PQ and take a point O on it.
(ii) Taking O as centre and convenient radius, mark an arc, which intersects PQ at A and B.
(iii) Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
(iv) Join OR. Thus, ∠QOR = ∠POQ = 90° .
(v) Draw OD the bisector of ∠POR. Thus, ∠QOD is required angle of 135°.

Question 6: Draw an angle of measure 45° and bisect it.
Solution
Steps of construction:
(a) Draw a line PQ and take a point O on it.
(b) Taking O as centre and a convenient radius, draw an arc which intersects PQ at two points A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(d) Join OC. Then ∠COQ is an angle of 90°
(e) Draw OE as the bisector of ∠COE. Thus, ∠QOE = 45°
(f) Again draw OG as the bisector of ∠QOE. Thus, ∠QOG = ∠EOG = 

Question 7: Draw an angle of measure 135° and bisect it.
Solution
Steps of construction:
(a) Draw a line PQ and take a point O on it.
(b) Taking O as centre and convenient radius, mark an arc, which intersects PQ at A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
(d) Join OR. Thus, ∠QOR = ∠POQ = 90° .
(e) Draw OD the bisector of ∠POR. Thus, ∠QOD is required angle of 135° .
(f) Now, draw OE as the bisector of ∠QOD. Thus, ∠QOE = ∠DOE = 

Question 8: Draw an angle of 70° Make a copy of it using only a straight edge and compasses.
Solution
Steps of construction:

(a) Draw an angle 70° with protractor, i.e., ∠POQ = 70°
(b) Draw a ray AB.
(c) Place the compasses at O and draw an arc to cut the rays of ∠POQ at L and M.
(d) Use the same compasses, setting to draw an arc with A as centre, cutting AB at X.
(e) Set your compasses setting to the length LM with the same radius.
(f) Place the compasses pointer at X and draw the arc to cut the arc drawn earlier at Y.
(g) Join AY. Thus, ∠YAX = 70°
Question 9: Draw an angle of 40° . Copy its supplementary angle.
Solution
Steps of construction:

(a) Draw an angle of 40° with the help of protractor, naming ∠AOB.
(b) Draw a line PQ.
(c) Take any point M on PQ.
(d) Place the compasses at O and draw an arc to cut the rays of ∠AOB at L and N.
(e) Use the same compasses setting to draw an arc O as centre, cutting MQ at X.
(f) Set your compasses to length LN with the same radius.
(g) Place the compasses at X and draw the arc to cut the arc drawn earlier Y.
(h) Join MY.
Thus, ∠QMY = 40° and ∠PMY is supplementary of it.
