NCERT Solutions for Chapter 4 Basic Geometrical Ideas Class 6 Maths

Basic Geometrical Ideas Questions and Answers
Chapter Name | Basic Geometrical Ideas NCERT Solutions |
Class | CBSE Class 6 |
Textbook Name | Maths |
Related Readings |
|
Exercise 4.1
Question 1:

(a) Five points
(b) A line
(c) Four rays
(d) Five line segments
Solution

Question 2: Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.
(a) Line containing point E.
(b) Line passing through A.
(c) Line on which O lies.
(d) Two pairs of intersecting lines.

Solution

Question 4: How many lines can pass though:
(a) one given point?
(b) two given points
Solution
(a) Infinite number of lines can pass through one given point.

(b) Only one line can pass through two given points.
Question 5: Draw a rough figure and label suitably in each of the following cases:

Solution

Question 6:


Solution
(a) True
(b) True
(c) True
(d) False
(e) False
(f) False
(g) True
(h) False
(i) False
(j) False
(k) True
Exercise 4.2
Question 1: Classify the following curves as
(i) Open or
(ii) Closed.

Solution
(a) Open curve
(b) Closed curve
(c) Open curve
(d) Closed curve
(e) Closed curve
Question 2: Draw rough diagrams to illustrate the following:
(a) Open curve
(b) Closed curve
Solution
(a) Open curves:

(b) Closed curves

Question 3: Draw any polygon and shade its interior.
Solution
Polygon ABCDE

Question 4: Consider the given figure and answer the questions:
(a) Is it a curve?
(b)Is it closed?

Solution
(a) Yes, it is a curve.
(b) Yes, it is closed.
Question 5: Illustrate, if possible, each one of the following with a rough diagram:
(a) A closed curve that is not a polygon.
(b) An open curve made up entirely of line segments.
(c) A polygon with two sides.
Solution

(c) Polygon with two sides cannot be draw.
Exercise 4.3
Question 1: Name the angles in the given figure:
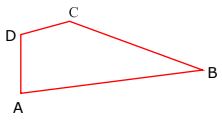
solution
There are four angles in given figure:
∠ABC,
∠CDA,
∠DAB,
∠DCB
Question 2: In the given diagram, name the point(s):
(a) In the interior of ∠DOE.
(b) In the exterior of ∠EOF.
(c) On ∠EOF.

Solution
(a) Point interior of ∠DOE : A
(b) Points exterior of ∠EOF: C, A, D
(c) Points on ∠EOF: E, O, B, F
Question 3: Draw rough diagrams of two angles such that they have:
(a) One point in common.
(b) Two points in common.
(c) Three points in common.
(d) Four points in common.
(e) One ray in common.





Question 1: Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?
Solution

A is neither interior of the figure nor exterior of triangle. It is a vertex.
Question 2: (a) Identify three triangles in the figure:
(b) Write the names of seven angles.
(c) Write the names of sic line segments.
(d) Which two triangles have ∠B as common?

Solution
(a) The three triangles are: △ABC, △ABD, △ADC
(b) Angles are: ∠ADB, ∠ADC, ∠ABD, ∠ACD, ∠BAD, ∠CAD, ∠BAC
(d) Triangles having common ∠B: △ABC, △ABD,
Exercise 4.5
Question 1: Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
Solution

Diagonal PR and diagonal SQ meet at O, which is inside the quadrilateral.
Question 2: Draw a rough sketch of a quadrilateral KLMN. State:
(a) Two pairs of opposite sides.
(b) Two pairs of opposite angles.
(c) Two pairs of adjacent sides.
(d) Two pairs of adjacent angles.
Solution
(a) Pair of opposite sides : KL and MN, KN and LM
(b) Pair of opposite angles : ∠K and ∠M, ∠L and ∠N
(c) Pair of adjacent sides : KN and NM, KL and LM
(d) Pair of adjacent angles : ∠K and ∠N,∠L and ∠M

Question 3: Investigate:
Use strip and fasteners to make a triangle and a quadrilateral.
Try to push inward at any one vertex of the triangle. Do the same to the quadrilateral.
Is the triangle distorted? Is the quadrilateral distorted? Is the triangle rigid?
Why is it that structures like electric towers make use of triangular shapes and not quadrilateral?
Solution
O is common to both the angles ∠AOC and ∠BOC.
No, the triangle is not distorted but the quadrilateral is distorted and also the triangle is rigid.
Structures like electric towers make use of triangular shape so that they could not be distorted and they could be rlgid.
Exercise 4.6
Question 1:

From the above figure, identify:
(a) The centre of circle.
(b) Three radii.
(c) A diameter.
(d) A chord.
(e) Two points in the interior.
(f) A point in the exterior.
(g) A sector.
(h) A segment.
Solution

(a) O is the centre.
(b) Three radii: OA, OB and OC
(c) A diameter: AC
(d) A chord: ED
(e) Interior points: O, P
(f) Exterior point: Q
(g) A sector: OAB
(h) A segment: ED
Question 2: (a) Is every diameter of a circle also a chord?
(b) Is every chord of a circle also a diameter?
Solution
(a) Yes, every diameter of a circle is also a chord.
(b) No, every chord of a circle is not a diameter.
Question 3: Draw any circle and mark:
(a) Its centre.
(b) A radius.
(c) A diameter.
(d) A sector.
Solution
(a) Its centre is O.
(b) A radius is OB.
(c) A diameter is AC.
(d) A sector OAB.

Question 4: Say true or false:
(a) Two diameters of a circle will necessarily intersect.
(b) The centre of a circle is always in its interior.
Solution
(a) True
(b) True
