NCERT Exemplar Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry and its Equation Exercise 8.4

Chapter 8 Introduction to Trigonometry and its Equation NCERT Exemplar Solutions Exercise 8.4 Class 10 Maths

Chapter Name	NCERT Maths Exemplar Solutions for Chapter 8 Introduction to Trigonometry and its Equation Exercise 8.4
Book Name	NCERT Exemplar for Class 10 Maths
Other Exercises	Exercise 8.1 Exercise 8.2 Exercise 8.3
Related Study	NCERT Solutions for Class 10 Maths

Exercise 8.4 Solutions

Long Answer Questions

1. If cosecθ + cotθ = p, then prove that cosθ = (p² – 1)/(p² + 1) . 

Solution

As, 
cosecθ + cot θ = p

2. Prove that √(sec² θ + cosec² θ) = tan θ + cot θ.

Solution

Taking, 
L.H.S = √(sec² θ + cosec² θ)
Since, 

3. The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.

Solution

Let us take PR = h meter, the height of the tower.
The distance between the observer and tower is QR = (20 +x) m, 
where 
QR = QS + SR 
= 20 + x
∠PQR = 30°
∠ PSR = θ
In ∆PQR,
tan 30° = h/(20 +x )
⇒ 1/√3 = h/(20 + x)
On cross multiplication, 
We get, 
20 + x = √3h 
⇒ x = √3h - 20 ...eq. (i) 
In ∆PSR, 
tan θ = h/x
As, angle of elevation increases by 15°  when the observer moves 20 m towards the tower.
So,
θ = 30° + 15° = 45°
Therefore,
tan 45° = h/x
⇒ 1 = h/x 
⇒ h = x 
Putting x = h in eq. (i), 
h = √3h - 20 
⇒ √3h - h = 20 
⇒ h(√3 - 1) = 20 
On rationalizing we get, 
h = 10(√3 + 1)
The required height of the tower is 10(√3 + 1) meter.

4. If  1 + sin² θ = 3sin θ cosθ,  then prove that tan θ = 1 or 1/2. 

Solution

We have, 
 1 + sin² θ = 3sin θ cosθ 
on dividing L.H.S and R.H.S equations with sin² θ, 
We get, 

cosec² θ + 1 = 3 cot θ
Also, 
cosec² θ - cot² θ = 1
⇒ cosec² θ = cot² θ +1
⇒ cot² θ +1+1 = 3 cot θ
⇒ cot² θ +2 = 3 cot θ
⇒ cot² θ –3 cot θ +2 = 0
We split the middle term and then solve the equation,
cot² θ – cot θ –2 cot θ +2 = 0
⇒ cot θ(cot θ -1)–2(cot θ +1) = 0
⇒ (cot θ – 1)(cot θ – 2) = 0
⇒ cot θ = 1, 2
We have, 
tan θ = 1/cotθ
tan θ = 1, 1/2
Proved !! 

5. Given that sinθ + 2cosθ = 1, then prove that 2sinθ - cosθ = 2.

Solution

We have, 
sinθ + 2 cosθ = 1
Squaring on both sides, 
(sinθ + 2cosθ)² = 1 
⇒ sin² θ + 4cos² θ + 4 sinθ cosθ = 1 
Also, 
sin² θ = 1 - cos² θ
and 
cos² θ = 1 - sin² θ
⇒ (1 - cos² θ) + 4(1 - sin² θ) + 4sin θ cosθ = 1
⇒ 1 – cos² θ + 4 – 4 sin² θ + 4sin θcos θ = 1
⇒ –4 sin² θ – cos² θ + 4sin θcos θ = –4
⇒ 4 sin² θ + cos² θ – 4sin θcos θ = 4
Also,
a² + b² - 2ab = (a - b)² 
So,
(2sin θ – cos θ)² = 4
⇒ 2sin θ – cos θ = 2
Proved

6. The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st. 

Solution

Let BC = s; 

PC = t 
Let height of the tower be AB = h. 

∠ABC = θ and

∠APC = 90° – θ

(∵ the angle of elevation of the top of the tower from two points P and B are complementary)

In ABC, 
tan θ = AC/BC 
= h/s  ...(i) 
In APC, 
tan(90 - θ) = AC/PC 
= h/t
cotθ = h/t  ...(ii)
So, multiplying (i) and (ii), 
tanθ × cot θ = h/t × h/s 
⇒ 1 = h² /st 
⇒ h²  = st 
⇒ h = √st
Therefore, the height of the tower is √st.

7. The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.

Solution

Let SQ = h be the tower.

∠SPQ = 30° and

∠SRQ = 60°

As given in the question, the length of shadow is 50 m long hen angle of elevation of the sun

is 30° than when it was 60°. So,

PR = 50 m and

RQ = x m

In SRQ, 
tan 60° = h/x 
⇒ √3 = h/x 
⇒ x = h/√3
In SPQ, 
tan 30° = h/(50 + x)
1/√3 = h(50 + x)
⇒ 50 + x = √3h
Putting value of x, 
50 + h/√3 = √3h
⇒ 50√3 + h = 3h  
⇒ 50√3 = 3h - h 
⇒ 3h - h = 50√3
⇒ 2h = 50√3
⇒ h = 25√3
So, the required height is 25√3 m.

8. A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is  (h tanα)/(tanβ - tanα).

Solution

We have, a vertical flag staff of height h is surmounted on a vertical tower of height let (H), 
so that, 
FP = h and 
FO = H.

The angle of elevation of the bottom and top of the flag staff on the plane is ∠PRO = α and

∠FRO = β respectively.

In ∆PRO, we have,
tanα = PO/RO 
= h/x 
x = h/tan α  ...(i) 
In FRO, 
tanβ = FO/RO
⇒ tanβ = (FP + PO)/RO 
⇒ tanβ = (H + h)/x 
⇒ x = (H+h)/tanβ  ...(ii) 
From (i) and (ii), 
(H + h)/tanβ = h/tanα
On solving, 
H = (h tanα)/(tanα + tanβ) 
Hence, proved

9. If tanθ + secθ = l, then prove that secθ = (l² + 1)/2l .

Solution

Given:

tanθ + secθ =  l  ...eq.(i)

Multiplying and dividing by (sec θ – tan θ) on numerator and denominator of L.H.S,

So, 
secθ - tanθ = 1/l   ...eq. (ii) 
Adding eq. (i) and eq.(ii), we get 
(tanθ + secθ) + (secθ - tanθ) = l + 1/l 
Adding eq. (i) and eq. (ii), we get 
(tanθ + secθ) + (secθ - tanθ) = l + 1/l 
So, 
secθ =  (l² + 1)/2l . 

Hence, proved. 

10. If sinθ + cosθ = p and secθ + cosecθ = q, then prove that q(p² - 1) = 2p. 

Solution

Given that, 
sinθ + cosθ = p ...(i) 
and 
secθ + cosecθ = q 

Since, sinθ + cosθ = p
On squaring both sides, we get 
(sinθ + cosθ)² = p² 
(sin² θ + cos² θ) + 2sinθ cosθ = p² 
[as, (a + b)² = a² + 2ab + b² ]
1 + 2sinθ cosθ = p² 
⇒ 1 + 2(p/q) = p² 
⇒ q + 2p = p²q
⇒ 2p = p²q - q
⇒ q(p² - 1) = 2p 

11. If  a sinθ + bcosθ = c, the prove that a cosθ - b sinθ = √(a² + b² - c²)

Solution

Given that, 
a sinθ + b cosθ = c 
On squaring both sides, 
(a + sinθ + cosθ b)² = c² 

⇒ a² sin² θ + b² cos² θ + 2ab sinθ cosθ = c² 

⇒ a² (1 - cos² θ) + b² ( 1 - sin² θ) + 2ab sinθ . cosθ = c² 

⇒ a² - a² cos² θ + b² - b² sin² θ + 2absinθ . cosθ = c² 
⇒ a² + b² - c² = a² cos² θ + b² sin² θ - 2absinθ.cosθ
⇒ a² + b² - c²  = a² cos² θ + b² sin² θ - 2absinθ.cosθ
⇒ a² + b² - c²  = (acosθ - bsinθ)² 
[as, a² + b² - 1ab = (a- b)²]
⇒ a cosθ - bsinθ = √(a² + b² - c² )

12. Prove that (1 + secθ - tanθ)/(1 + secθ + tanθ) = (1 - sinθ)/cosθ.

Solution

Taking LHS, 
On multiplying by (sec θ - tanθ) on numerator and denominator, 

13. The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.

Solution

Let us take the distance between the two towers = AB

= x m

and height of the other tower = PA

= h m

Given,

height of the tower = QB

= 30 m,

∠QAB = 60° and

∠PBA = 30°

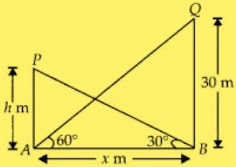
Now, in ΔQAB, 
tan 60 = QB/AB = 30/x 
⇒ √3 = 30/x 
⇒ x = 30/√3
⇒ x = 10√3
In PBA, 
tan 30 = PA/AB 
1/√3 = h/x
⇒ 1/√3 = h/10√3
⇒ h = 10 

14. From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α).  Find the distance between the two objects. 

Solution

Let the distance between the two objects is x m and CD = y m

Given,

∠BAX = α = ∠ABD

and

∠CAX = β = ∠ACD  [Alternate angle]

and

height of tower, AD = h m

In ACD, 
tan β = AD/CD
⇒ tanβ = h/y 
⇒ y = h/tanβ  ...(i) 
In ABD, 
tanα = AD/BD
⇒ tanα = AD/(BC + CD) 
⇒ tanα = h/(x + y) 
⇒ y = (h/tanα) - x  ...(ii) 
From (i) and (ii), 
(h/tanα) - x = h/tanβ
⇒ x = (h/tanα) - (h/tanβ)
⇒ x = h(cotα - cotβ)
Which is the required distance between the two objects. 

15. A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal. Show that p/q = (cos β - cos α)/(sinα - sinβ)

Solution

Let, 
OQ = x and 

OA = y 

Given, 
BQ = q, 
SA = P
and 

AB = SQ = Length of ladder

Also,

∠BAO = α and ∠QSO = β

cos α = OA/AB 
⇒ cos α = y/AB 
⇒ y = AB cos α = OA  ...(i) 
also, 
sinα = OB/AB 
⇒ OB = AB sinα 
In QSO, 
cos β = OS/SQ 
⇒ OS = SQ  cos β = AB cos β
and, 
sin β = OQ/SQ
⇒ OQ = SQ sin β = AB sinβ

Now, 
SA = OS - AO 
P = Ab(cos β - cos α )
Also, 
BQ = BO - QO

⇒ q = AB(sin α  - sin β)
So, 
p/q  = (cosβ - cos α)/(sin α - sinβ) 

16. The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower. 

Solution

Let the height the vertical tower be, 
OT = H m 

and 

OP = AB = xm

Given that, 

AP = 10 m

and

∠TPO = 60°,

∠TAB = 45°

Now, in ΔTPO, 
tan 60° = OT/OP 
⇒ tan 60° = H/x
⇒ x = h/√3
In TAB, 
tan 45° = TB/AB

⇒ 1 = (H - 10)/x 
⇒ x = H - 10 
Putting value of x, 
h/√3 = H - 10 
On solving, 
H = 5(√3 + 3)m

17. A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and  β, respectively. Prove that the height of the other house is h(1 + tan α cot β) metres. 

Solution

Let the height of the other house, 

OQ = H m and

OB = MW = x m

Given,

height of the first house = WB = h = MO

and ∠QWM = α,

∠OWM = β = ∠WOB  [Alternate angle]

Now, In ∆WOB,
tan β = WB/OB
⇒ tan β = h/x
⇒ x = h/tanβ  ...(i) 
In QWM, 
tan α = QM/WM

⇒ tan α = (OQ - MO)/WM

⇒ tan α = (H - h)/x 

⇒ x = (H - h)/tanα  ...(ii)
From (i) and (ii), 
(H - h)/tanα = h/tan β
On solving, 
H = h(1 + tanα × 1/tanβ) 

18. The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30°, respectively. Find the height of the balloon above the ground.

Solution

Let the height of the balloon from above the ground is H m 
and 
OP = W₂ R
= W₂ Q
= x m

Given, height of lower window from the ground = W₂ P
= 2m = OR 
Height of upper window from the lower window = W₁ W₂ 
= 4m = QR 

BQ = OB - (QR + RO)

= H - (4 + 2)

= H - 6

∠BW₁Q = 30° and

∠BW₂R = 60°

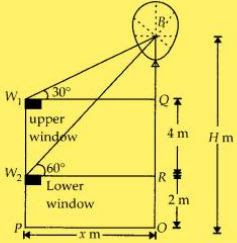
In BW₂ R, 
tan 60° = BR/W₂ R 
= (BQ + QR)/x 
⇒ √3 = [(H - 6) + 4]/x 
⇒ x = (H - 2)/√3  ...(i) 
In BW₁ R, 
tan 30° = BR/W₁ R
⇒ 1/√3 = (H - 6)/x 
⇒ x = √3(H - 6)  ...(ii) 
From (i) and (ii), 
√3(H - 6) = (H - 2)/√3 
On solving, 
H = 8m
The required height is 8m. 
Therefore, the required height of the balloon from the ground is 8m.