Chapter 8 Introduction to Trigonometry and its Equation NCERT Exemplar Solutions Exercise 8.2 Class 10 Maths

Chapter Name | NCERT Maths Exemplar Solutions for Chapter 8 Introduction to Trigonometry and its Equation Exercise 8.2 |
Book Name | NCERT Exemplar for Class 10 Maths |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 8.2 Solutions
Short Answer Questions with Reasoning:
Write ‘True’ or ‘False’ and justify your answer in each of the following:
1. tan 47°/cot 43° = 1
Solution
True
As, tan (90° - θ) = cot θ
tan 47°/cot 43° = [tan(90 - 43°)]/cot 43°
= cot 43°/cot 43°
= 1
2. The value of the expression (cos2 23° - sin2 67°) is positive.
Solution
False
As,
(a2 - b2 ) = (a + b)(a - b)
cos2 23° - sin2 67° =(cos 23°+sin 67°)(cos 23°-sin 67°)
= [cos 23°+sin(90°-23°)] [cos 23°-sin(90°-23°)]
= (cos 23°+cos 23°)(cos 23°-cos 23°)
(as, sin(90°-θ) = cos θ)
= (cos 23°+cos 23°).0
= 0,
And 0 is neither positive nor negative.
3. The value of the expression (sin 80° - cos 80°) is negative .
Solution
False
As,
sin θ increases when 0° ≤ θ ≤ 90°
Therefore,
(sin 80°-cos 80°) = (increasing value-decreasing value)
= a positive value.
So,
(sin 80°- cos 80°) > 0.
4. √[(1 - cos2 θ)sec2 θ = tanθ
Solution
True
5. If cos A + cos2 A = 1, then sin2 A + sin4 A = 1
Solution
True
As given in the question,
cos A + cos2 A = 1
⇒ cos A = 1 - cos2 A
Also,
sin2 θ+cos2 θ = 1
⇒ sin2 θ = 1- cos2 θ
So,
cos A = sin2 A ...(1)
Squaring L.H.S and R.H.S,
cos2 A = sin2 A ...(2)
Adding equations (1) and (2),
We get
sin2 A + sin4 A= cos A + cos2 A
So,
sin2 A+ sin4 A = 1
6. (tanθ + 2)(2tanθ + 1) = 5tanθ + sec2 θ
Solution
False
L.H.S
= (tan θ + 2) (2 tanθ+1)
= 2 tan2 θ + tanθ + 4 tanθ + 2
= 2 tan2 θ+5 tanθ + 2
As,
sec2 θ – tan2 θ = 1,
we get,
tan2 θ = sec2 θ - 1
= 2(sec2 θ-1) + 5 tanθ+2
= 2 sec2 θ - 2 + 5 tan θ+2
= 5 tanθ+ 2 sec2 θ
So,
L.H.S ≠ R.H.S
7. If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
Solution
False
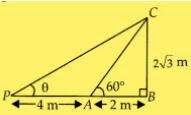
To understand the fact of this question, consider the following example
(i) A tower 2√3 m high casts a shadow 2m long on the ground, then the Sun's elevation is 60°
In ΔABC,
tan θ = BC/AB
⇒ tan θ = 2√3/2
⇒ tan θ = √3
⇒ tan θ = 60°
(ii) The A same height of tower casts a shadow 4m more from preceding point, then the Sun's elevation is 30°
In ΔPBC,
tanθ = CB/PB
⇒ tanθ = CB/(PA + AB)
⇒ tanθ = 2√3/(4+2)
⇒ tanθ = 2√3/6
⇒ tanθ = 1/√3
⇒ tanθ = 30°
Therefore, we conclude from above two examples that if the length of the shadow of a tower is increasing, then the angle of elevation of the Sun is decreasing.
8. If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
Solution
False
We can observe that, a man standing on a platform at point P, 3 m above the surface of a lake observes a cloud at point C.
Let the height of the cloud from the surface of the platform is h.
In MPC,
Then,
a + 1/a = 2 + 1/2
= 5/2
If 2sinθ = a + 1/a , then,
2sinθ = 5/2
⇒ sinθ = 5/4
= 1.25
Which is not possible.
⇒ a2 + b2 > 2ab
⇒ (a2 +b2 )/2ab > 1
cosθ = cosθ > 1 [as, cos θ = (a2 +b2 )/2ab]
Which is not possible. [as, -1 ≤ cosθ ≤ 1]
So, cosθ ≠ (a2 +b2 )/2ab
Case (i): Let us take the height of the tower is h In ΔABC, let BC = x m
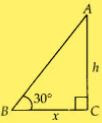
In ABC,
tan 30° = AC/BC
1/√3 = h/x ...(i)
Case (ii) : By condition, the height of the tower is doubled, PR = 2h,
In ΔPQR,
tanθ = PQ/QR
⇒ tanθ = 2h/x
⇒ tanθ = 2/x × x/√3 ...(from (i))
⇒ tanθ = 2/1 × 1/√3
⇒ tanθ = 1.15
⇒ θ = tan-1 (1.15)
which is less than 60°
So, the required angle is not doubled.
Let us take the height of a tower be h and the distance of the point of observation from its foot is x.
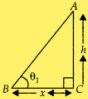
In ABC,
tan θ1 = AC/BC
= h/x ...(i)
Case (ii) :
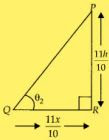
Now, the height of a tower increased by 10%
= h + 10% of h
= h + h× 10/100
= 11h/100
and the distance of the point of observation from its foot
= x + 10% of x
= 11x/10
In PQR,
tan θ2 = PR/QR
= (11h/10)/(11x/10)
= 4/x ...(ii)
From (i) and (ii),
tanθ1 = tanθ2