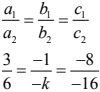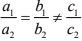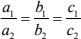Chapter 3 Pair of Linear Equation in Two Variables NCERT Exemplar Solutions Exercise 3.1 Class 10 Maths

Chapter Name | NCERT Maths Exemplar Solutions for Chapter 3 Pair of Linear Equation in Two Variables Exercise 3.1 |
Book Name | NCERT Exemplar for Class 10 Maths |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 3.1 Solutions
Choose the correct answer from the given four options in the following questions:
1. Graphically, the pair of equations
6x – 3y + 10 = 0
2x – y + 9 = 0 ;
Represents two lines which are:
(a) intersecting at exactly one point
(b) intersecting at exactly two points
(c) coincident at exactly two points
(d) parallel
Solution
(d)
a1 = 6
b1 = - 3
c1 = 10
a2 = 2
b2 = -1
c2 = 9
On solving, we get,
So, the linear equation has no solution and the two lines are parallel.
2. The pair of equations x + 2y + 5 = 0 and –3x – 6y + 1 = 0 have
(a) a unique solution
(b) exactly two solution
(c) infinitely many solutions
(d) no solution
Solution
On solving we get,
Therefore, the pair of equations has no solution.
3. If a pair of linear equations is consistent, then the lines will be,
(a) parallel
(b) always coincident
(c) intersecting or coincident
(d) always intersecting
Solution
(c) Intersecting or coincident
For linear equations to be consistent, we have following conditions,
4. The pair of equations y = 0 and y = -7 has
(a) one solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Solution
(d) no solution
The two equations above represents a pair of parallel lines. Therefore, there is no solution.
5. The pair of equations x = a and y = b graphically represents lines which are
(a) parallel
(b) intersecting at (b, a)
(c) coincident
(d) intersecting at (a, b)
Solution
(d) Intersecting at (a,b)
x = a is a straight line parallel to the y–axis.
Again,
y = b is a straight line parallel to the x–axis.
Therefore, the equations x = a and y = b graphically represents lines which intersects at (a, b).
Hence, (d) is the correct answer.
6. For what value of k do the equations 3x - y + 8 = 0 and 6x - ky = -16 represent coincident lines ?
(a) 1/2
(b) -1/2
(c) 2
(d) -2
Solution
(c) 2
3x - y = -18 ...(i)
6x - ky = -16 ...(ii)
For coincident lines,
On solving, we get,
k = 2.
7. If the line given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is
(a) -5/4
(b) 2/3
(c) 15/4
(d) 3/2
Solution
(c) 15/4
For parallel lines,
On solving we get,
4k = 15
⇒ k = 15/4
8. The value of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 will have infinity many solutions is
(a) 3
(b) –3
(c) –12
(d) No value
Solution
(d) no value
To have infinitely many solutions,
On solving, we get that there are no common values of c. Hence, there is no value of c for which the equations have infinitely many solutions.
9. One equation of a pair of dependent linear equations is –5x + 7y = 2. The second equation can be:(a) 10x + 14y + 4 = 0
(b) –10x – 14y + 4 = 0
(c)–10x + 14y + 4 = 0
(d) 10x – 14y = –4
Solution
(d) 10x - 14y = - 4
-2(-5x + 7y -2) = 0
-5x + 7y - 2 = 0 ...(i)
Let the second equation be,
a2x + b2y + c2 = 0 ...(ii)
∴ For dependent system of linear equations,
So,
a2 = -5k,
b2 = 7k
c2 = -2k
Putting value of k,
k = 0, and -1 it does not satisfy the required condition.
Let us take k = -2
So,
a2 = +10
b2 = -14
c2 = + 4
It satisfies the condition.
10. A pair of linear equations which has a unique solution x = 2, y = –3 is
(a) x + y = –1 and 2x – 3y = –5
(b) 2x + 5y = –11 and 4x + 10y = –22
(c) 2x – y = 1 and 3x + 2y = 0
(d) x – 4y –14 = 0 and 5x – y – 13 = 0
Solution
b and d both.
As x = 2, y = -3 is unique solution of system of equation so these values of must satisfy both equations.
(a) x + y = -1 and 2x - 3y = - 5
Putting x = 2 and y = 3 in both the equations.
LHS = x + y
2 - 3 = -1 (RHS)
LHS = 2x – 3y
= 2(2) –3(–3)
= 4 + 9
= 13
≠ RHS
(b) 2x + 5y = –11 and 4x + 10y = –22
Put x = 2 and y = –3 in both the equations.
LHS = 2x + 5y
= 2 × 2 + (–3)
= 4 – 15
= –11
= RHS
LHS = 4x + 10y
= 4(2) + 10(–3)
= 8 – 30
= –22
= RHS
(c) 2x – y = 1 and 3x + 2y = 0
Put x = 2 and y = –3 in both the equations.
LHS = 2x – y
2(2) + 3 = 7 ≠ RHS
LHS = 3x + 2y
= 3(2) + 1(–3)
= 6 – 6
= 0
= RHS
(d) x – 4y – 14 = 0 and 5x – y – 13 = 0
x – 4y = 14 and 5x – y = 13
Put x = 2 and y = –3 in both the equations.
LHS = x – 4y
= 2 – 4(–3)
= 2 + 12
= 14 = RHS
LHS = 5x – y
= 5(2) – (–3)
= 10 + 3
= 13 = RHS
So, the pair of equations is (b) and (d).