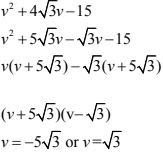NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials Exercise 2.3

Chapter 2 Polynomials NCERT Exemplar Solutions Exercise 2.3 Class 10 Maths

Chapter Name	NCERT Maths Exemplar Solutions for Chapter 2 Polynomials Exercise 2.3
Book Name	NCERT Exemplar for Class 10 Maths
Other Exercises	Exercise 2.1 Exercise 2.2 Exercise 2.4
Related Study	NCERT Solutions for Class 10 Maths

Exercise 2.3 Solutions

Short Answer Questions : 

Find the zeroes of the following polynomials by factorization method. 
1. 4x² – 3x - 1 
2. 3x²  + 4x - 4 
3. 5t² + 12t + 7 
4. t³ - 2t² - 15t 
5. 2x² + 7x/2 + 3/4 
6. 4x² + 5√2x - 3 
7. 2s³ - (1 + 2√2)s + √2 
8. v² + 4√3 v - 15 
9. y² + 3/2 √5 y - 5 
10. 7y² - 11y/3 - 2/3 

Solution

1. 4x² - 3x - 1 
By splitting the middle term, 
4x² - 4x + 1x - 1 
Now, taking out the common factors, 
4x(x - 1) + 1 (x - 1)
= (4x + 1)(x - 1 
The zeroes are, 
4x + 1 = 0 
⇒ 4x = - 1
⇒ x = -1/4
Also, 
(x - 1) = 0 
⇒ x = 1 
Therefore, zeroes are -1/4 and.

2. 3x² + 4x - 4

Solution

3x² + 4x - 4 
By splitting the middle term, we get, 
3x² + 6x - 2x - 4 
= 3x(x + 2) - 2(x + 2)
= (x + 2)(3x - 2) 
Either, 
x +2 = 0 
⇒ x = - 2
⇒ 3x - 2 =  0
⇒ 3x = 2 
⇒ x = 2/3 
Therefore, zeroes are 2/3 and -2.

3. 5t² + 12t + 7 

Solution

5t² + 12t + 7
By splitting the middle term, we get, 
5t² + 5t + 7t + 7 
= 5t(t + 1) + 7(t + 1)
= (t + 1)(5t + 7)
So, the zeroes, are, 
t + 1 = 0
⇒ t = -1
⇒ 5t + 7 = 0 
⇒ 5t = -7
⇒ t = -7/5 
So, the zeroes are -7/5 and -1

4. t³ - 2t² - 15t 

Solution

t³ - 2t² - 15t 
t(t² - 2t - 15)
Splitting the middle term of the equation t² - 2t - 15, we get, 
t(t² - 5t + 3t - 15)
= t(t(t- 5) + 3 (t - 5)
= t(t + 3)(t- 5)
The zeroes are, 
t + 3 = 0
⇒ t = -3 
t - 5 = 0 
⇒ t = 5 
So, zeroes are 0, 5 and -3. 

5. 2x² + 7x/2 + 3/4 

Solution

2x² + 7x/2 + 3/4 
We can write this equation as, 
8x² + 14x + 3 
Now, splitting the middle term, we get, 
8x² + 12x + 2x + 3 
= 4x(2x + 3) + 1 (2x + 3)
= (4x + 1)(2x + 3)
The zeroes are, 
4x + 1 = 0 
⇒ x = -1/4 
⇒ 2x + 3 = 0 
⇒ x = -3/2
Therefore, zeroes are -1/4 and -3/2. 

6. 4x² + 5√2x - 3

Solution

By splitting middle term, we get, 
4x² + 5√2x - 3 
= 4x² + 6√2x - √2x - 3 
= 2√2x(√2x + 3) - 1(√2x + 3)
= (2√2x - 1)(√2x + 3)
Therefore, 
x = 1/2√2
or, 
x = -3/√2 

7. 2s³ - (1 + 2√2)s + √2

Solution

By splitting middle term, we get, 

8. v² + 4√3 v - 15 

Solution

By splitting middle term, we get, 

9.  y² + 3/2 √5 y - 5 

Solution

By splitting middle term, we get, 

10. 7y² - 11y/3 - 2/3 

Solution

By splitting middle term, we get,