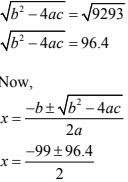Chapter 2 Polynomials NCERT Exemplar Solutions Exercise 2.1 Class 10 Maths

Chapter Name | NCERT Maths Exemplar Solutions for Chapter 2 Polynomials Exercise 2.1 |
Book Name | NCERT Exemplar for Class 10 Maths |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 2.1 Solutions
Multiple Choice Questions:
1. Choose the correct answer from the given four options in the following questions:
If one of the zeroes of the quadratic polynomial (k - 1)x2 + kx + 1, is -3, then the value of k is
(A) 4/3
(B) -4/3
(C) 2/3
(D) -2/3
Solution
(A) 4/3
It is given in the question,
-3 is one of the zeros of quadratic polynomial (k -1)x2 + kx + 1.
Putting -3 in the given polynomial,
(k - 1)(-3)2 + k(-3) + 1 = 0
⇒ (k -1)9 + k(-3) + 1 = 0
⇒ 9k - 9 - 3k + 1 = 0
⇒ 6k - 8 = 0
⇒ k = 8/6
Or,
k = 4/3
2. A quadratic polynomial, whose zeroes are -3 and 4, is
(A) x2 - x + 12
(B) x2 + x + 12
(C) x2 /2 - x/2 - 6
(D) 2x2 + 2x - 24
Solution
(C) x2 /2 - x/2 - 6
Justification :
Sum of zeroes, α+ β= -3+4 =1
Product of Zeroes, αβ = -3× 4 -12
So, the quadratic polynomial becomes,
x2 - (sum of zeroes) x + (product of zeroes)
= x2 - (α+ β) x+ (αβ)
= x2 – (1) x + (-12)
= x2 – x -12
= x2/2 - x/2 - 6
3. If the zeroes of the quadratic polynomial x2 + (a + 1)x + b are 2 and -3, then
(A) a = -7, b = -1
(B) a = 5, b = -1
(C) a = 2, b = -6
(D) a = 0, b = -6
Solution
(D) a = 0, b = -6
The zeroes of the polynomial = 2 and -3,
Putting, x = 2 in x2 + (a + 1)x + b
22 + (a + 1)(2) + b = 0
⇒ 4 + 2a + 2 + b = 0
⇒ 6 + 2a + b = 0
⇒ 2a + b = -6
Now Putting x = -3 in equation.
(-3)2 + (a + 1)(-3) + b = 0
9 – 3a-3 + b = 0
6 – 3a+b = 0
-3a+b = -6 ...(ii)
Subtracting equation (ii) from (i)
2a+b – (-3a+b) = -6-(-6)
⇒ 2a + b + 3a - b = -6+6
⇒ 5a = 0
⇒ a = 0
Putting the value of ‘a’ in equation (i),
2a + b = -6
⇒ 2(0) +b = -6
⇒ b = -6
4. The number of polynomials having zeroes as -2 and 5 is
(A) 1
(B) 2
(C) 3
(D) more than 3
Solution
(D) More than 3
Explanation:
It is given in the question, the zeroes of the polynomials are -2 and 5.
The polynomial is the form of
p(x) = ax2 + bx + c
Sum of the zeroes = – (coefficient of x) ÷ coefficient of x2
Sum of the zeroes = -b/a
-2 + 5 = -b/a
⇒ 3 = -b/a
⇒ b = -3
and
a = 1
Also,
Product of zeroes = c/a
(-2) × 5 = c/a
⇒ -10 = c (as, a = 1)
Putting the values of a, b and c in the polynomial p(x) = ax2 + bx + c.
We get,
x2 - 3x - 10
Hence, we can conclude that x can have any value.
5. Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is
(A) -c/a
(B) c/a
(C) 0
(D) -b/a
Solution
(B) c/a
Justification:
We have the polynomial,
ax2 + bx2 + cx + d
Sum of product of roots of a cubic equation is given by c/a.
It is given that one root = 0
Now, let the other roots be α, β
αβ + β(0) + (0)α = c/a
⇒ αβ = c/a
Hence the product of other two roots is c/a
6. If one of the zeroes of the cubic polynomial x3 +ax2 + bx + c is -1, then the product of the other two zeroes is
(A) b - a + 1
(B) b - a - 1
(C) a - b + 1
(D) a - b - 1
Solution
(A) b - a + 1
Taking, f(x) = x3 + ax2 + bx + c
Also,
Zero of f(x) is -1 so f(-1) = 0
(-1)3 + a(-1)2 + b(-1) + c = 0
⇒ -1 + a – b + c = 0
⇒ a – b + c = 1
⇒ c = 1 + b – a
Now,
α. β. γ = -d/a
⇒ -1βγ = -c/1
⇒ βγ = c
⇒ βγ = 1 + b - a
7. The zeroes of the quadratic polynomial x2 + 99x + 127 are
(A) both positive
(B) both negative
(C) one positive and one negative
(D) both equal
Solution
(B) both negative
Taking,
f(x) = x2 + 99x + 127
Now,
b2 - 4ac = (99)2 - 4× 1×127
⇒ b2 - 4ac = 9801 - 508
Therefore, both roots will be negative as 99 > 96.4
8. The zeroes of the quadratic polynomial x2 + kx + k, k ≠ 0,
(A) cannot both be positive
(B) cannot both be negative
(C) are always unequal
(D) are always equal
Solution
(A) cannot both be positive
Taking,
f(x) = x2 + kx + k
To find the zeroes of f(x), we take,
f(x) = 0
x2 + kx + k = 0
Here one root is positive, and the other root is negative.
So, the roots cannot be both positive.
9. If the zeroes of the quadratic polynomial ax2 + bx + c, c ≠ 0 are equal, then
(A) c and a have opposite signs
(B) c and b have opposite signs
(C) c and a have that same sign
(D) c and b have the same sign
Solution
(C) c and a have the same sign
For equal roots b2 - 4ac = 0
As, b2 is always positive so 4ac must be positive or we can say product of a and c must be positive i.e., a and c must have same sign either positive or negative.
10. If one of the zeroes of a quadratic polynomial of the form x2 + ax + b is the negative of the other, then it
(A) Has no linear term and the constant term is negative.
(B) Has no linear term and the constant term is positive.
(C) Can have a linear term but the constant term is negative.
(D) Can have a linear term but the constant term is positive.
Solution
(A) Has no linear term and the constant term is negative.
Taking,
f(x) = x2 + ax + b
Let, α, β are the roots of it.
Then,
β = -α (Given)
Therefore, f(x) = x2 + b shows that it has no linear term and constant term is negative.
11. Which of the following is not the graph of a quadratic polynomial ?
Solution
(D)
Graph ‘D’ intersect at three points on X-axis so the roots of polynomial of graph is three, so it is cubic polynomial. Other graph are of quadratic polynomial.