RD Sharma Solutions for Class 9 Chapter 22 Tabular Representation of Statistical Data Exercise 22.1

Chapter 22 Tabular Representation of Statistical Data RD Sharma Solutions Exercise 22.1 Class 9 Maths

Chapter Name	RD Sharma Chapter 22 Tabular Representation of Statistical Data Exercise 22.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 22.2
Related Study	NCERT Solutions for Class 10 Maths

Exercise 22.1 Solutions

1. What do you understand by the word “statistics” in
(i) Singular form
(ii) Plural form?

Solution

The word “Statistics” is used in both its singular as well as its plural senses.
(i) In singular sense: Statistics may be defined as the science of collection, presentation, analysis and interpretation of numerical data
(ii) In plural sense: Statistics means numerical facts or observations collected with definite purpose
(iii) For example: Income and expenditure of persons in a particular locality, number males and females in a particular town are statistics.

2. Describe some fundamental characteristics of statistics.

Solution

Fundamental characteristics of statistics:
(i) A single observation does not form statistics are a sum total of observation
(ii) Statics are expressed quantitatively not qualitatively
(iii) Statistics are collected with definite purpose
(iv) Statistics in an experiment are comparable and can be classified various groups.

3. What are (i) primary data? (ii) secondary data? Which of the two – the primary or the secondary data – is more reliable and why?

Solution

The word data means information statistical data and of two types
(i) Primary data, (ii) Secondary data
(i) Primary data: when an investigator collects data himself with a definite plan or design in his (her) mind is called primary data
(ii) Secondary data: data which are not originally collected rather obtained from published or unpublished sources are known as secondary data. Secondary data are collected by an individual or an institution for some purpose and are used by someone else in another context.
Primary data are reliable and relevant because they are original in character and are collected by some individuals or by research bodies.

4. Why do we group data?

Solution

The data obtained in original form are called raw data. Raw data does not give any useful information and is rather confusing to mind. Data is grouped so that it becomes understandable can be interpreted. According to various characteristics groups are formed by us. After grouping the data, we are in position to make calculations of certain values which will help us in describing and analyzing the data.

5. Explain the meaning of the following terms:
(i) Variable
(ii) Class-integral
(iii) Class-size
(iv) Class-mark
(v) Frequency
(vi) Class limits
(vii) True class limits

Solution

(i) Variable: Any character that can vary from one individual to another is called variable or variable

(ii) Class interval: In the data each group into which raw data is considered is called a class-interval.

(iii) Class-size: The different between the true upper limit and lower limit is called the class size of that class.

(iv) Class mark: The middle value of the class is called as the class mark.
Class mark = (Upper Limit + Lower Limit)/2 

(v) Frequency: The number of observations corresponding to class is called its frequency.

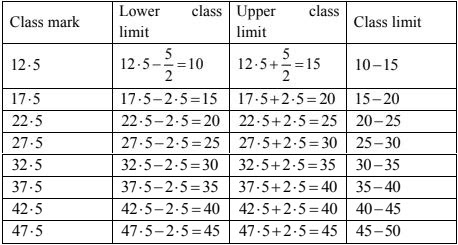
(vi) Class limits: Each class is bounded by two figures, called the class limits. The figures on the left side of the classes are called lower limits while figures on the right side are called upper limits.

(vii) True class limits: if classes are inclusive eg 15 - 19, 20 - 24, 25 - 29, 30 - 34 ........
Then, true lower limit of class = upper limit of class - 0.5 
And true upper limit of class = upper limit of class + 0.5
Example : true limits of the class 15 - 19 are 14.5 and 19.5 
But if because classes are exclusive use like 10 - 20, 20 - 30, 30 - 40 ........
Here class limits and true class limits are the same. 

6. The ages of ten students of a group are given below. The ages have been recorded in years and months :
8 - 6, 9 - 0, 8 - 4, 9 - 3, 7 - 8, 8 - 11, 8 - 7, 9 - 2, 7- 10, 8 - 8 
(i) What is the lowest age ? 
(ii) What is the highest age ?
(iii) Determine the range ? 

Solution

The ages of ten students of a group are given below
8 - 6, 9 - 0, 8 - 4, 9 - 3, 7 - 8, 8 - 11, 8 - 7, 9 - 2, 7- 10, 8 - 8 
(i) Lowest age is 7 years, 8 months 
(ii) Highest age is 9 years, 3 months. 
(iii) Range = highest age - lowest age 
= 9 year, 3 months, 7 year, 8 months 
= 1 year, 7 months 

7. The monthly pocket money of six friends is given below: Rs. 45, Rs.30, Rs. 40, Rs. 50, Rs. 25, Rs. 45.
(i) What is the highest pocket money?
(ii) What is the lowest pocket money?
(iii) What is the range?
(iv) Arrange the amounts of pocket money in ascending order.

Solution

The monthly pocket money of six friends is given below:
Rs. 45, Rs.30, Rs. 40, Rs. 50, Rs. 25, Rs. 45.
(i) Highest pocket money = Rs. 50 
(ii) Lowest pocket money = Rs. 25
(iii) Range = 50 - 25 = 25 .
(iv) The cumulative amounts of pocket money in ascending order is 
Rs. 25, Rs. 30, Rs. 40, Rs. 45, Rs. 45, Rs. 50.

8. Write the class-size in each of the following : 
(i) 0 - 4, 5 -9, 10 -14
(ii) 10 - 19, 20 - 29, 30 - 39
(iii) 100 - 120, 120 - 140, 160 - 180 
(iv) 0 - 0.25, 0.25 - 0.50, 0.50 - 0.75 
(v) 5 - 5.01, 5.01 - 5.02, 5.02 - 5.03

Solution

(i) 0 - 4, 5 - 9, 10 - 14
True class limits are 0.5 - 4.5, 4.5 - 9.5,  9.5 - 14.5.
∴ Class size = 14.5 - 9.5 = 5 

(ii) 10 - 19, 20- 29, 30 - 39
True class limits → 10.5 - 19.5, 19.5 - 29.5, 29.5 - 39.5
Class  size = 39.5 - 29.5 = 10

(iii) 100 - 120, 120 - 140, 160 - 180.
Here the class limits and true class limits are the same
∴ Class size = 120 - 100 = 20 

(iv) 0 - 0.25, 25 - 0.50, 0.50 - 0.75 
Here the class limits and true class limits are the same 
∴ Class size = 0.25 - 0 = 0.25

(v) 5 - 5.01, 5.01 - 5.02, 5.02 - 5.03. 
Here the class limits and true class limits are the same 
∴ Class size = 5.01 - 5.0 = 0.01.

9. The final marks in mathematics of 30 students are as follows :
53, 61, 48, 60, 78, 68, 55, 100, 67, 90
75, 88, 77, 37, 84, 58, 60, 48, 62, 56
44, 58, 52, 64, 98, 59, 70, 39, 50, 60
(i) Arrange these marks in the ascending order, 30 to 39 one group, 40 to 49 second group etc. Now answer the following:
(ii) What is the highest score?
(iii) What is the lowest score?
(iv) What is the range?
(v) If 40 is the pass mark how many have failed?
(vi) How many have scored 75 or more?
(vii) Which observations between 50 and 60 have not actually appeared?
(viii) How many have scored less than 50?

Solution

The final marks in mathematics of 30 students are as follows:
53, 61, 48, 60, 78, 68, 55, 100, 67, 90, 75, 88, 77, 37, 84, 58, 60, 48, 62, 56, 44, 58, 52, 64, 98, 59, 70, 39, 50, 60.

(i)	Group	Observations
	I(30 – 39)	37, 39
	II(40 – 49)	44, 48, 48
	III(50 – 59)	50, 52, 53, 55, 56, 58, 59
	IV(60 – 69)	60, 60, 60, 61, 62, 64, 67, 68
	V(70 – 79)	70, 55, 77, 78
	VI(80 – 89)	84, 88
	VII(90 – 99)	90, 98
	VIII(100 – 109)	100

(ii) Highest score = 100

(iii) Lowest score = 37 

(iv) Range = 100 - 37 = 63

(v) If 40 is the pass mark, 2 students have failed

(vi) 8 students have scored 75 or more

(vii) Observation 51, 54, 57 between 50 and 60 have not actually appeared

(viii) 5 students have scored less than 50

10. The weights of new born babies (in kg) in a hospital on a particular day are as follows:

2.3, 2.2, 2.1, 2.7, 2.6, 3.0, 2.5, 2.9, 2.8, 3.1, 2.5, 2.8, 2.7, 2.9, 2.4

(i) Rearrange the weights in descending order.

(ii) Determine the highest weight.

(iii) Determine the lowest weight.

(iv) Determine the range.

(v) How many babies were born on that day?

(vi) How many babies weigh below 2.5 kg?

(vii) How many babies weigh more than 2.8 kg?

(viii) How many babies weigh 2.8 kg?

Solution

The weights of new born babies (in kg) area as follows

2.3, 2.2, 2.1, 2.7, 2.6, 3.0, 2.5, 2.9, 2.8, 3.1, 2.5, 2.8, 2.7, 2.9, 2.4
(i) The weights in descending order 

3.1, 3.0, 2.9, 2.9, 2.8, 2.8, 2.7, 2.7, 2.6, 2.5, 2.5, 2.4, 2.3, 2.2, 2.1.
(ii) The highest weight = 3.1 kg 

(iii) The lowest weight = 2.1 kg 

(iv) Range = 3.1 - 2.1 = 1.0 kg 

(v) 15 babies were born on that particular day 

(vi) 4 babies weight below 2.5 kg 

(vii) Weight more than 2.8 kg are 4 - babies. 

(viii) Weight 2.8 kg → 2 babies 

11. The number of runs scored by a cricket player in 25 innings are as follows : 

26, 35, 94, 48, 82, 105, 53, 0, 39, 42, 71, 0, 64, 1.5, 34, 67, 0, 42, 124, 84, 54, 48, 139, 64, 47.

(i) Rearrange these runs in ascending order.

(ii) Determine the player, is highest score.

(iii) How many times did the player not score a run?

(iv) How many centuries did he score?

(v) How many times did he score more than 50 runs?

Solution

The numbers of runs scored by a player in 25 innings are 

26, 35, 94, 48, 82, 105, 53, 0, 39, 42, 71, 0, 64, 15, 34, 15, 34, 67, 0, 42, 124, 84, 54, 48, 139,

64, 47 

(i) Runs in ascending order are 0, 0, 0, 15, 26, 34, 35, 39, 42, 42, 47, 48, 48, 53, 54, 64,

64, 67, 71, 82, 84, 94, 105, 124, 139.

(ii) The highest number = 139

(iii) The player did not score any run 3 times

(iv) He scored 3 centuries

(v) He scored more than 50 run 12 times.

12. The class size of a distribution is 25 and the first class-interval is 200-224. There are seven

class-intervals.

(i) Write the class-intervals.

(ii) Write the class-marks of each interval.

Solution

Given, 

Class size = 25 
First class interval  = 200 - 224 
(i) Seven class intervals are : 
200 - 240, 225 - 249, 250 - 274, 275 - 299, 300 - 324, 325 - 349, 350 - 374.

13. Write the class size and class limits in each of the following:

(i) 104, 114, 124, 134, 144, 154, and 164

(ii) 47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97 and 102

(iii) 12.5, 17.5, 22.5, 27.5, 32.5, 37.5, 42.5, 47.5

Solution

(i) 104, 114, 124, 134, 144, 154 and 102

Class size = 114 – 104 = 10 

(ii) 47, 52, 57, 62, 67, 72, 79, 82, 87, 92, 97, 1102

Class size = 52 - 47 = 5

(iii) Class size = 17.5 - 12.5 = 5 

14. Following data gives the number of children in 40 families:

1, 2, 6, 5, 1, 5, 1, 3, 2, 6, 2, 3, 4, 2, 0,0,4,4,3,2,2,0,0,1,2,2,4,3, 2,1,0,5,1,2,4,3,4,1,6,2,2.

Represent it in the form of a frequency distribution.

Solution

15. The marks scored by 40 students of class IX in mathematics are given below:

81, 55, 68, 79, 85, 43, 29, 68, 54, 73, 47, 35, 72, 64, 95, 44, 50, 77, 64, 35, 79, 52, 45, 54, 70, 83, 62, 64, 72, 92, 84, 76, 63, 43, 54, 38, 73, 68, 52, 54.

Prepare a frequency distribution with class size of 10 marks.

Solution

16. The heights (in cm) of 30 students of class IX are given below:

155, 158, 154, 158, 160, 148, 149, 150, 153, 159, 161, 148, 157, 153, 157, 162, 159, 151, 154, 156, 152, 156, 160, 152, 147, 155, 163, 155, 157, 153.

Prepare a frequency distribution table with 160-164 as one of the class intervals.

Solution

17. The monthly wages of 30 workers in a factory are given below:

83.0, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 836, 878, 840, 868, 890, 806, 840, 890.

Represent the data in the form of a frequency distribution with class size 10.

Solution

18. The daily maximum temperatures (in degree celsius) recorded in a certain city during the

month of November are as follows:

25.8, 24.5, 25.6, 20.7, 21.8, 20.5, 20.6, 20.9, 22.3, 22.7, 23.1, 22.8, 22.9, 21.7, 21.3, 20.5, 20.9, 23.1, 22.4, 21.5, 22.7, 22.8, 22.0, 23.9, 24.7, 22.8, 23.8, 24.6, 23.9, 21.1

Represent them as a frequency distribution table with class size 1°C.

Solution

19. Construct a frequency table with equal class intervals from the following data on the monthly

wages (in rupees) of 28 laborers working in a factory, taking one of the class intervals as

210-230 (230 not included):

220, 268, 258, 242, 210, 268, 272, 242, 311, 290, 300, 320, 319, 304, 302, 318, 306, 292, 254, 278, 210, 240, 280, 316, 306, 215, 256, 236.

Solution

20. The daily minimum temperatures in degrees Ce1siu& recorded in a certain Arctic region are as follows:

−12.5, −10.8, −18.6, −8.4, −10.8, −4.2, −4.8, −6.7, −13.2, −11.8, −2.3, 1.2, 2.6, 0, 2.4, 0, 3.2, 2.7, 3.4, 0, − 2.4, − 2.4, 0, 3.2, 2.7, 3.4, 0, − 2.4, − 5.8, -8.9, 14.6, 12.3, 11.5, 7.8, 2.9.

Represent them as frequency distribution table taking −19.9 to −15 as the first class

interval.

Solution

Since first class interval is frequency distribution with lower limit included and upper limit excluded is 

21. The blood groups of 30 students of class VIII are recorded as follows:

A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O

Represent this data in the form of a frequency distribution table. Find out which is the most

Common and which is the rarest blood group among these students.

Solution

Here 9 students have blood groups A, 6 as B,3 as AB and as O.

So the table representing the data is as follows

As 12 students have the blood group O and 3 have their blood group is AB. Clearly, the most

common blood group among these students is 0 and the rarest blood group among these

students is 0 and the rarest blood group among these students is AB

22. Three coins were tossed 30 times. Each time the number of head occurring was noted down as follows : 

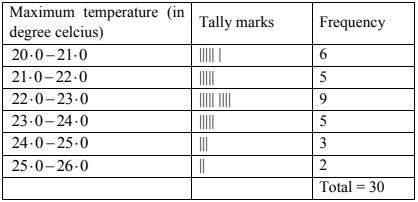
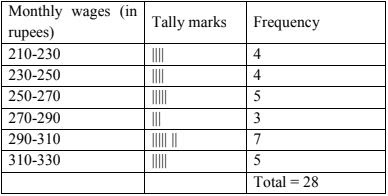
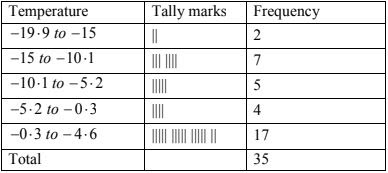
0	1	2	2	1	2	3	1	3	0
1	3	1	1	2	2	0	1	2	1
3	0	0	1	1	2	3	2	2	0

Solution

By observing the data given above following frequency distribution table can be constructed

Number of heads	Number of times (frequency)
0	6
1	10
2	9
3	5
Total	30

23. Thirty children were asked about the number of hours they watched T.V. programmers in the previous week. The results were found as follows : 

1	6	2	3	5	12	35	8	4	8
10	3	4	12	2	8	15	1	17	6
3	2	8	5	9	6	8	7	14	12

(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class intervals as 5 - 10. 

(ii) How many children watched television for 15 or more hours a week ?

Solution

Class intervals will be 0 - 5, 5 - 10, 10 - 15, ......
The grouped frequency distribution table is as follows 

Hours	Number of children
0 - 5	10
5 - 10	13
10 - 15	5
15 - 20	2
Total	30

(ii) The number of children, who watched TV for 15 or more hours a week is 2(i.e., number of children in class interval 15 - 20).