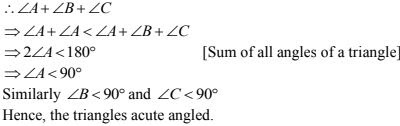RD Sharma Solutions for Class 9 Chapter 9 Triangles and its Angles Exercise 9.1

Chapter 9 Triangles and its Angles RD Sharma Solutions Exercise 9.1 Class 9 Maths

Chapter Name	RD Sharma Chapter 9 Triangles and its Angles Exercise 9.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	No Other Exercises
Related Study	NCERT Solutions for Class 10 Maths

Exercise 9.1 Solutions

1. In a ΔABC, if ∠A = 55°, ∠B = 40° , find ∠C. 

Solution

Given ∠A = 55° , ∠B = 40 then ∠C = ?
We know that 
In  a ΔABC sum of all angles of triangle is 180°
i.e., ∠A + ∠B + ∠C = 180°
⇒ 55° + 40° + ∠C = 180°
⇒ 95° + ∠C = 180°
⇒ ∠C = 180° - 95°
⇒ ∠C = 85°

2. If the angles of a triangles are in the ratio 1 : 2 : 3, determine three angles. 

Solution

Given that the angles of a triangle are in the ratio 1 : 2 : 3 
Let the angles be a, 2a, 3a
∴ We know that 
Sum of all angles of triangles is 80°
a + 2a + 3a = 180°
⇒ 6a = 180°
⇒ a = 180°/6
⇒ a = 30°
Since a = 30°
2a = 2(30°) = 60°
3a = 3(30°) = 90°
∴ angles are a = 30°, 2a = 60°, 3a = 90°
∴ Hence angles are 30°, 60° and 90°

3. The angles of a triangle are (x - 40)° , (x - 20)° and (x/2 - 10)° . Find the value of x. 

Solution

Given that 
The angles of a triangle are 
(x - 40)° , (x - 20)°  and (x/2 - 10)°
We know that 
Sum of all angles of triangle is 180°

4. The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is 10° , find the three angles. 

Solution

Given that,
The difference between two consecutive angles is  10° .
Let x, x + 10, x + 20 be the consecutive angles differ by  10°
W.K.T sum of all angles of triangle is 180° .
x + x + 10 + x + 20 = 180°
3x + 30 = 180°
⇒ 3x = 180 - 30°
⇒ 3x = 150°
⇒ x = 50°
x = 50°
The required angles are
x, x + 10 and x + 20
x = 50°
⇒ x + 10 = 50 + 10 = 60
⇒ x + 20 = 50 + 10 + 10 = 70
The difference between two consecutive angles is 10° then three angles are 50°, 60° and 70°.

5. Two angles of a triangle are equal and the third angle is greater than each of those angles by 30°. Determine all the angles of the triangle. 

Solution

Given that, 
Two angles are equal and the third angle is greater than each of those angles by  30° .
Let x, x, x + 30 be the angles of a triangle 
We know that 
Sum of all angles of a triangle is 180°
x + x + x + 30 = 180°
3x + 30 = 180°
⇒ 3x = 180° - 30°
⇒ 3x = 150°
⇒ x = 150°/3
⇒ x = 50°
∴ The angles are x, x, x + 30
x = 50°
⇒ x + 30 = 80°
∴ The required angles are 50°, 50°, 80°.

6. If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right triangle.

Solution

If one angle of a triangle is equal to the sum of other two 

i.e., ∠B = ∠A + ∠C
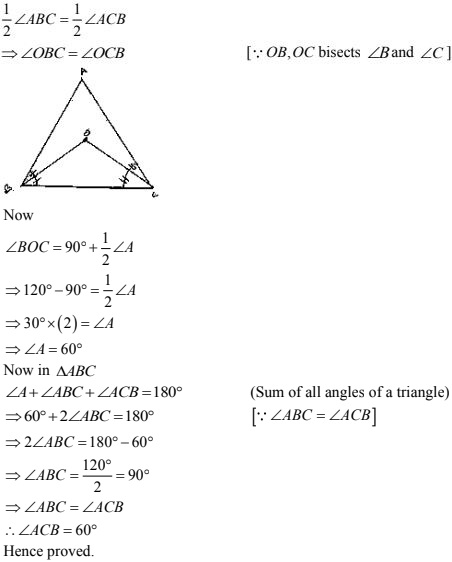
Now, in ΔABC

(Sum of all angles of triangle 180°)
∠A + ∠B + ∠C = 180°
⇒ ∠B + ∠B = 180° [∵ ∠B = ∠A + ∠C]

⇒ 2∠B = 180°
⇒ ∠B = 180°/2

⇒ ∠B = 90° 

∴ ABC is a right angled a triangle. 

7.  ABC is a triangle in which ∠A -72° , the internal bisectors of angles B and C meet in O. 

Find the magnitude of ∠ROC. 

Solution

8. The bisectors of base angles of a triangle cannot enclose a right angle in any case. 

Solution

In a  ΔABC 

Sum of all angles of triangles is 180°

i.e.,  ∠A + ∠B + ∠C = 180° divide both sides by '2' .

9. If the bisectors of the base angles of a triangle enclose an angle of 135°, prove that the triangle is a right triangle.

Solution

Given the bisectors the base angles of an triangle enclose an angle of  135°
i.e., ∠BOC = 135° 
But, W.K.T

∴ ΔABC is right angled triangle right angled at A. 

10. In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120. Show that ∠A = ∠B = ∠C = 60°. 

Solution

Given,

In ΔABC 

∠ABC = ∠ACB 

Divide both sides by '2'

11. Can a triangle have : 

(i) Two right angles ?

(ii)  Two obtuse angles ? 

(iii) Two acute angles ? 

(iv) All angles more than 60° ? 

(v) All angles less than 60° ? 

(vi) All angles equal to 60° ?

Justify your answer in each case. 

Solution

(i) No

Two right angles would up to 180°. So, the third angle becomes zero. This is not possible, so a triangle cannot have two right angles.

[Since sum of angles in a triangle is 180°]

(ii) No

A triangle can’t have 2 obtuse angles. Obtuse angle means more than 90°. So, that the sum of the two sides will exceed 180° which is not possible. As the sum of all three angles of a triangle is 180°.

(iii) Yes

A triangle can have 2 acute angle. Acute angle means less the 90° angle.

(iv) No

Having angles-more than 60° make that sum more than 180° which is not possible.

[∵ The sum of all the internal angles of a triangle is 180°]

(v) No 

Having all angles less than 60° will make that sum less than 180° which is not possible.

[∵ The sum of all the internal angles of a triangle is 180°.]

12. If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled. 

Solution

Given each angle of a triangle less than the sum of the other two