Chapter 8 Lines and Angles RD Sharma Solutions Exercise 8.2 Class 9 Maths

Chapter Name | RD Sharma Chapter 8 Lines and Angles Exercise 8.2 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 8.2 Solutions
1. In the below Fig, OA and OB are opposite rays:
(i) If x = 25°, what is the value of y ?
(ii) If y = 35° , what is the value of x ?
Solution

2. In the below fig, write all pairs of adjacent angles and all the linear pairs.
Solution
Adjacent angles are
(i) ∠AOC, ∠COB
(ii) ∠AOD, ∠BOD
(iii) ∠AOD, ∠COD
(iv) ∠BOC, ∠COD
Linear pairs : ∠AOD, ∠BOD, ∠AOC, ∠BOC.
3. In the given below Fig, find x. Further find ∠BOC, ∠COD and ∠AOD.
Solution
Since ∠AOD and ∠BOD are form a line pair
∠AOD + ∠BOD = 180°
∠AOD + ∠COD + ∠BOC = 180°
Given that
4. In the given below fig, rays OA, OB, OC, OP and OE have the common end point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360 °.

Solution
Given that
Rays OA, OB, OD and OE have the common end point O.
A ray of opposite to OA is drawn
Since ∠AOB, ∠BOF are linear pairs
∠AOB + ∠BOF = 180°
∠AOB + ∠BOC + ∠COF = 180° ...(1)
Also
Also
∠AOE, ∠EOF are linear pairs
∠AOE + ∠EOF = 180°
∠AOE + ∠DOF + ∠DOE = 180° ...(2)
By adding (1) and (2) equations we get
∠AOE + ∠DOF + ∠DOE = 180° ...(2)
By adding (1) and (2) equations we get
∠AOB + ∠BOC + ∠COF + ∠AOE + ∠DOF + ∠DOE = 360°
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°
Hence proved.
5. In the below Fig, ∠AOC and ∠BOC form a linear pair. if a - 2b = 30°, find a and b.

Solution
Given that,
∠AOC and ∠BOC form a linear pair
If a - 2b = 30°
∠AOC = a°, ∠BOC = b°
∴ a + b = 180° ...(i)
Given a - 2b = 30°...(ii)
By subtracting (i) and (ii)
∴ a + b = 180° ...(i)
Given a - 2b = 30°...(ii)
By subtracting (i) and (ii)
a + b - a + 2b = 180° - 30°
⇒ 3b = 150°
⇒ b = 150°/3
⇒ b = 150°/3
⇒ b = 50°
Hence a - 2b = 30°
a - 2(50)° = 30° [∵ b = 50°]
Hence a - 2b = 30°
a - 2(50)° = 30° [∵ b = 50°]
a = 30° + 100°
a = 130°
∴ a = 130° , b = 50° .
a = 130°
∴ a = 130° , b = 50° .
6. How many pairs of adjacent angles are formed when two lines intersect in a point?
Solution
Four pairs of adjacent angle formed when two lines intersect in a point they are
∠AOD, ∠DOB
∠AOD, ∠DOB
∠DOB, ∠BOC
∠COA, ∠AOD
∠BOC, ∠COA
Hence 4 pairs
7. How many pairs of adjacent angles, in all can you name in below fig.?

Solution
Pairs of adjacent angles are
∠ EOC, ∠DOC
∠EOD, ∠DOB
∠DOC, ∠COB
∠EOD, ∠DOA
∠DOC, ∠COA
∠BOC, ∠BOA
∠BOA, ∠BOD
∠BOA, ∠BOE
∠EOC, ∠COA
∠EOC, ∠COB
∴ Hence 10 pairs of adjacent angles
8. In below fig, determine the value of x.

Solution
Since sum of all the angles round a point is equal to 360° . Therefore
⇒ 3x + 3x + 150 + x = 360°⇒ 7x = 360° - 150°
⇒ 7x = 210°
⇒ x = 210°/7
⇒ x = 30°
9. In the below fig, AOC is a line, find x.

Solution
Since ∠AOB and ∠BOC are linear pairs
∠AOB + ∠BOC = 180°
⇒ 70° + 2x° = 180°
⇒ 2x° = 180° - 70°
⇒ 2x = 110°
⇒ x = 110°/2
⇒ x = 55°
10. In the below fig, POS is a line, find x.

Solution
Since ∠POQ and ∠QOS are linear pairs
∠POQ + ∠QOS = 180°
⇒ ∠POQ + ∠QOR + ∠SOR = 180°
⇒ 60° + 4x° + 40° = 180°
⇒ 4x° = 180° - 100°
⇒ 4x° = 80°
⇒ x =20°
⇒ 4x° = 80°
⇒ x =20°
11. In the below fig, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.

Solution
Here, ∠ACD + ∠BCD = 180°
[Since ∠ACD, ∠BCD are linear pairs]
∠ACD = 5x, ∠BCD = 4x
⇒ 5x +4x = 180°
⇒ 9x = 180°
⇒ 5x +4x = 180°
⇒ 9x = 180°
⇒ x = 20°
∴ x = 20°
∴ x = 20°
12. Given ∠POR = 3x and ∠QOR =2x + 10, find the value of x for which POQ will be a line.
(Below fig).

Solution
Since ∠QOR, ∠POP are linear pairs
∠QOR + ∠POR = 180°
⇒ 2x + 10 + 3x = 180° [∵ ∠QOR = 2x + 10, ∠POR = 3x]
⇒ 5x + 10 = 180°
⇒ 5x = 180° - 10
⇒ 5x = 170°
⇒ x = 34°
⇒ x = 34°
13. In Fig. 8.42, a is greater than b by one third of a right - angle. Find the values of a and b.

Solution
Since a, b are linear pair
⇒ a + b = 180°
⇒ a = 180° - b ...(1)
⇒ a = 180° - b ...(1)
Now,
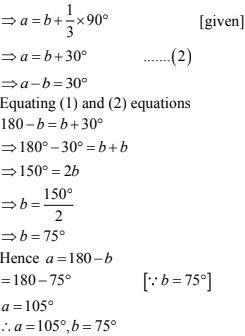
14. What value of y would make AOB a line in below fig, if ∠AOC = 4y and ∠BOC = (6y + 30)

Solution

15. If below fig, ∠AOF and ∠FOG form a linear pair.

∠EOB = ∠FOC = 90 and ∠DOC = ∠FOG = ∠AOB = 30
(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
Solution

16. In below fig, OP, OQ, OR and OS arc four rays. Prove that :
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°


Solution
Given that
OP, OQ, OR and OS are four rays
You need to produce any of the ray OP, OQ, OR, and OS backwards to a point in the figure.
Let us produce ray OQ backwards to a point
T so that TOQ is a line
Ray OP stands on the TOQ
Since ∠TOP, ∠POQ is linear pair
∠TOP, + ∠POQ = 180° ...(1)
Similarly, ray OS stands on the line TOQ
∠TOS + ∠SOQ = 180° ...(2)
But ∠SOQ = ∠SOR + ∠QOR
So, (2), becomes
∠TOS + ∠SOR + ∠OQR = 180°
Now, adding (1) and (3) you get
∠TOP + ∠POQ + ∠TOS + ∠SOR + ∠QOR = 360°
⇒ ∠TOP + ∠TOS = ∠POS
∴ (4) becomes
∴ (4) becomes
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
17. In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
Given,
Ray OS stand on a line POQ
Ray OR and Ray OT are angle bisectors of ∠POS and ∠SOQ respectively
∠POS = x
∠POS and ∠QOS is linear pair
∠POS + ∠QOS = 180°
x + ∠QOS = 180°
∠QOS = 180° - x
Now, ray or bisector ∠POS

18. In the below fig, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ - 5 : 7, find all the angles.

Solution
Given ∠POR and ∠ROP is linear pair.
∠POR + ∠ROP = 180°
Given that
∠POR : ∠ROP = 5 : 7


Solution
Given that, OR perpendicular.
∴ POR = 90°
∴ POR = 90°






