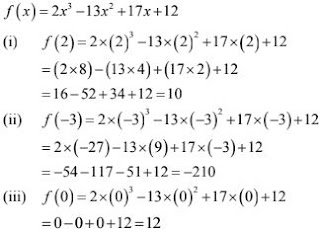Chapter 6 Factorisation of Algebraic Expressions RD Sharma Solutions Exercise 6.2 Class 9 Maths

Chapter Name | RD Sharma Chapter 6 Factorisation of Polynomials Exercise 6.2 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 6.2 Solutions
1. If f(x) = 2x3 - 13x2 + 17x + 12, find (i) f(2) (ii) f(-3) (iii) f(0)
Solution
We have
2. Verify whether the indicated numbers are zeroes of the polynomials corresponding to them in the following cases :
(i) f(x) = 3x + 1, x = -1/3
(ii) f(x) = x2 - 1, x = 1, -1
(iii) g(x) = 3x2 - 2, x = 2/√3, -2/√3
(iv) p(x) = x3 - 6x2 + 11x -6, x = 1, 2, 3
(v) f(x) = 5x - π, x = 4/5
(vi) f(x) = x2 and x = 0
(vii) f(x) = lx + m, x = -m/l
(viii) f(x) = 2x + 1, x = 1/2
Solution
(i) f(x) = 3x + 1, x = -1/3
We have
f(x) = 3x + 1
Solution

4.If x = -1/2 is a zero of the polynomial p(x) = 8x3 - ax2 - x + 2, find the value of a.
Solution

5. If x = 0 and x = -1 are the roots of the polynomial f(x) = 2x3 - 3x2 + ax + b, find the value of a and b.
Solution

6. Find the integral roots of the polynomial f(x) = x3 + 6x2 + 11x + 6 .
Solution
We have
f(x) = x3 + 6x2 + 11x + 6
Clearly, f(x) is a polynomial with integer coefficient and the coefficient of the highest degree term i.e., the leading coefficients is 1.
Therefore, integer roots of f(x) are limited to the integer factors of 6, which are ±1, ±2, ±3, ±6
We observe that

f(x) = x3 + 6x2 + 11x + 6
Clearly, f(x) is a polynomial with integer coefficient and the coefficient of the highest degree term i.e., the leading coefficients is 1.
Therefore, integer roots of f(x) are limited to the integer factors of 6, which are ±1, ±2, ±3, ±6
We observe that

7. Find rational roots of the polynomial f(x) = 2x3 + x2 - 7x - 6
Solution
We have
f(x) = 2x3 + x2 - 7x - 6
Clearly, f(x) is a cubic polynomial with integer coefficient. If b/c is a rational roots in lowest terms, then the value of b are limited to the factors of 6 which ±1, ±2, ±3, ±6 and values of c are limited to the factors of 2 which are ±1, ±2.
Hence , the possible rational roots of f(x) are ±1, ±2, ±3, ±6, ±1/2, ±3/2
We observe that

f(x) = 2x3 + x2 - 7x - 6
Clearly, f(x) is a cubic polynomial with integer coefficient. If b/c is a rational roots in lowest terms, then the value of b are limited to the factors of 6 which ±1, ±2, ±3, ±6 and values of c are limited to the factors of 2 which are ±1, ±2.
Hence , the possible rational roots of f(x) are ±1, ±2, ±3, ±6, ±1/2, ±3/2
We observe that